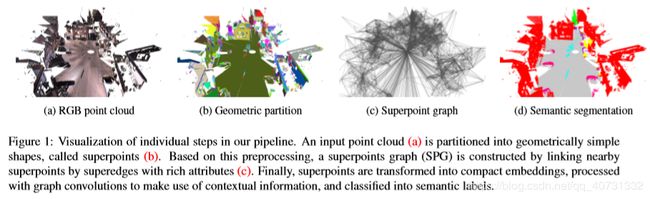
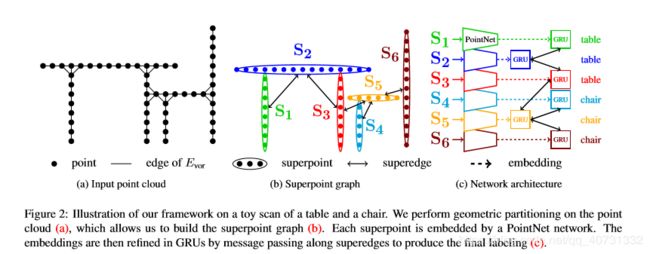
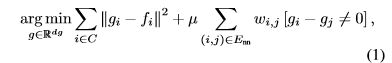【点云】Large-scale Point Cloud Semantic Segmentation with Superpoint Graphs

目录

1 摘要

2 介绍

3 方法

3.1 基于全局能量的集合分割

3.2 建立超点图

3.3 嵌入超点

3.4上下文分割

---

1 摘要

我们提出一个基于深度学习的框架，来解决大规模点云的语义分割问题。我们认为点云的组织形式可以被SPG（Superpoint Graph）有效的捕获，SPG是从被分割为几何均匀部分的扫描场景中得到。SPGs提供了一个紧凑但是充足的目标上下文关系的表示，并可以被应用到图卷积网络。

 

2 介绍

大规模点云的语义分割有大量挑战，这些困难阻碍了卷积神经网络的应用：（1）大规模数据；（2）没有明确的组织结构（图片的规则网格）。前人希望将CNN结构在图片分割中的成功应用复制到点云数据上，比如：（1）SnapNet: 将点云转换为一系列二维RGBD快照，对快照的语义切割可以应用到原数据上。（2）SegCloud: 在规则体素网格中使用三维卷积。

然而，我们认为这些方法没有捕捉到点云数据的固有结构，因此限制了描述的表现。将点云转换为二维格式会带来信息的损失，并且要求做表面再卷积，这和语义分割一样难。点云的体积表示是低效的，并会丢失细节。还有很多特别为点云设计的深度学习模型，表现不错，但是受限于输入数据的尺寸。

我们提出了一种大规模点云的表示方式，简单形状（超级点）内在联系的集合，是用于图像语义分割的超级像素的迁移。这种结构可以被属性有向图（SPG）捕获，它的结点代表简单形状，边描述了结点被丰富的边特征描述的邻近关系。

SPG有很多优点：

（1）取代了去对单个点或体素的分类，SPG关注整个目标部分，这更容易被分类

（2）SPG可以细节地描述邻近物品的关系，这对上下文分类很重要：车总是在路上，天花板总是被墙所环绕。

（3）SPG的大小被简单结构的数量所决定而不是点云中点的数量，这少了好几个量级。

这使得我们可以将大规模内在关系模型化。我们的贡献如下：

（1）我们介绍了SPG，一种全新的点云表示方式，带有丰富的边特征，表征了点云部分间的上下文关系。

（2）基于这种表达，我们可以在大规模点云上应用深度学习，而不需要牺牲细节，我们的结构包括PointNets，用于超级点的嵌入和图卷积，以及上下文分割。并且我们介绍了一种全新的、更高效的以边为条件的卷积（ECC），和一种新得输入门格式GRU

 

3 方法

我们主要想解决点云的大小问题。点云往往包含上亿个点，使得很难直接使用深度学习方法。我们提出的SPG表示使得我们将语义分割问题划分为三个不同的问题。

（1）几何同质分割：将点云分割为简单但富有意义的几何形状。这个无监督步骤，将所有点云作为输入，因此必须被高效地计算。通过这个分割，SPG可以被简单地计算。

（2）Superpoint嵌入：SPG的每个点都关联于点云的一个小的部分，我们假设这部分是语义同质的。通过降采样，最多数百个点可以代表这些初始部分。减小输入点云的规模，使得我们可以使用PointNet。

（3）上下文分割：SPG比任何其他在初始点云上建立的图更小。基于图卷积的深度学习方法可以用大量的边特征（促进了特征大范围的互动）对点分类。

 

3.1 基于全局能量的集合分割

我们的目标不是分离出像车、椅子这样的实际个体，而是这些更简单、共有的抽象部分。我认为这一步类似于图像中设计卷积核提取特征，只不过这里使用的是无监督方法。注意，这一步是完全无监督的，并且没有使用分类的标签。

输入点云C，有n个点，每个点，被它的三维位置，或者，其他观察值，比如颜色、强度所定义。对每个点，我们计算个集合特征，描述了局部邻近的形状。我们使用：线性，平面性和散射（linearity, planarity, scattering）。我们也计算了每个点的高度，定义为pi在整个输入点云归一化坐标中的。

Global energy由10最近邻邻接图Gnn = (C, Enn)。几何同质分割定义为以下优化问题解的常数连通分量。

其中[·]是Iverson bracket（艾佛森括号，如果括号内的条件满足则为1，不满足则为0），边w的权值随边的长度线性递减。因子μ是正则化强度，它决定了结果划分的粗糙程度。

要使全局最小，（1）gi应该尽可能等于fi；（2）gi应该尽可能等于gj。具体来说，（1）希望gi尽可能的“代表”fi；（2）希望gi, gj尽可能相同。带来的结果就是，使得尽可能多的特征相似的点的g值相同。最后，g值相同的点被视作一个Superpoint。全部的点被划分为：。

 

3.2 建立超点图

，其中S是超点，是超边代表超点间的邻接关系。超边由df个特征，描述了超点间的邻接关系。F是特征矩阵。

 

对称Vorinoi邻接图。如果在Evor中至少存在一条边，连接两个超点S和T，则S和T有邻接关系。

超边特征描述：

各超点间点的位置的协方差矩阵的特征按降序排序：

Length(S) = λ1

Surface(S) = λ1λ2

Volume(S) = λ1λ2λ3

 

3.3 嵌入超点

为了保证批处理的效率和数据扩充的方便，我们将实时采样的超级点降至np = 128点。因为PointNet的max-pooling操作，降采样并不会影响效果。但我们也观察到当超点的点数少于nminp = 40时，效果变差。

为了让PointNet学习不同形状的空间分布，在嵌入前，每个超点被重新标为单位球。点被正则化距离，观察值，oi和几何特征表示。为了为了保持形状大小的协变，超点的原始公制直径，在PointNet的max-pooling之后被连接使用，作为额外的特征。最后每个超点Si嵌入PointNet得到一个dz维的向量zi。

 

3.4上下文分割

我们的方法基于Gated Graph Neural Networks和Edge-Conditioned Convolutions。总的来说，超点根据超边的信息片段来改进它们的嵌入。

参考：https://blog.csdn.net/Dujing2019/article/details/104091750