自然语言处理（NLP）：11 SelfAttention和transformer Encoder情感分析

动手写SelfAttetion和transformer Encoder模型实现电影情感分类

通过代码学习，加深对Self Attention 和 Transformer 模型实现理解

• 数据预处理分析，掌握torchtext 在数据预处理应用

• Self Attention 机制模型训练
  $$a_{ts}=emb(x_t{)}^{T}emb(x_s)$$
  $${\alpha }_t\propto \exp (\sum _s{a}_{ts})$$
  $$h_{self}=\sum _t{a}_{t}emb(x_t)$$
  $$\sigma (w^T{h}_{self})$$
  $$\sigma (w^T(h_{self}+h_{avg}))$$

• 基于Transformer Encoder 代码动手训练情感分类

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d_k}})V$$
$$P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{\text{model}}})$$

$$P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{\text{model}}})$$

$$\begin{gathered} \mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}(Q,K,V)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_1,...,\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_{\mathrm{h}})W^O \\ \text{where}\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_{\mathrm{i}}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V) \end{gathered}$$

• transformer 模型论文以及代码实现

The Annotated Transformer

Attention Is All You Need

导入库

import torch
import torch.nn as nn

import pandas as pd
import numpy as np
from torchtext import data
import random

SEED = 1234

torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print('device = ',device)

device =  cpu

数据预处理

数据分析

简单了解下我们的数据分布

train = pd.read_csv('data/senti.train.tsv',sep='\t',header=None,names=['data','label'])
val = pd.read_csv('data/senti.dev.tsv',sep='\t',names=['data','label'])
test = pd.read_csv('data/senti.test.tsv',sep= '\t',names=['data','label'])

train.head()

	data	label
0	hide new secretions from the parental units	0
1	contains no wit , only labored gags	0
2	that loves its characters and communicates som...	1
3	remains utterly satisfied to remain the same t...	0
4	on the worst revenge-of-the-nerds clichés the ...	0

查看数据是否存在空的数据字段: 感觉数据还不错，不会出现nan 的数据

train.info()

RangeIndex: 67349 entries, 0 to 67348
Data columns (total 2 columns):
data     67349 non-null object
label    67349 non-null int64
dtypes: int64(1), object(1)
memory usage: 1.0+ MB

val.info()

RangeIndex: 872 entries, 0 to 871
Data columns (total 2 columns):
data     872 non-null object
label    872 non-null int64
dtypes: int64(1), object(1)
memory usage: 13.7+ KB

test.info()

RangeIndex: 1821 entries, 0 to 1820
Data columns (total 2 columns):
data     1821 non-null object
label    1821 non-null int64
dtypes: int64(1), object(1)
memory usage: 28.5+ KB

我们看下整体数据样本分布

print('训练数据集数量： ',train.shape[0])
print('验证数据集数量： ',val.shape[0])
print('测试数据集数量： ',test.shape[0])

训练数据集数量：  67349
验证数据集数量：  872
测试数据集数量：  1821

不同标签数据分布，看类别数据是否均衡：每个数据标签分类还不错

train['label'].value_counts()

1    37569
0    29780
Name: label, dtype: int64

val['label'].value_counts()

1    444
0    428
Name: label, dtype: int64

test['label'].value_counts()

0    912
1    909
Name: label, dtype: int64

加载数据

• 通过TabularDataset 来定义我们的数据集,目前支持格式包括 csv, tsv, 和 json files ，同时可以借助 splits (train, validation, test) 加载不同的数据集

  • 参考 torchtext 提供的案例：https://torchtext.readthedocs.io/en/latest/examples.html

• Field 定义文本和Label 的类型

• torchtext 使用参考代码

  • https://github.com/bentrevett/pytorch-sentiment-analysis/blob/master/1%20-%20Simple%20Sentiment%20Analysis.ipynb
  • https://github.com/keitakurita/practical-torchtext/blob/master/Lesson%201%20intro%20to%20torchtext%20with%20text%20classification.ipynb

声明Fields

# 声明Fields
from torchtext.data import Field
tokenize = lambda x: x.split()# 指定文本字段分词方法（中文的话可以jieba） 
TEXT = Field(sequential=True, batch_first=True, include_lengths=True)
# batch_first=True 加载数据第一个维度batch_size，如果不设置默认max_seq_len
# include_lengths=True 表示后续text 中包括文本实际长度信息
LABEL = Field(sequential=False, use_vocab=False,dtype=torch.float)

创建我们的Dataset

# 创建我们的Dataset
from torchtext.data import TabularDataset
train, val, test = TabularDataset.splits(
        path="data", # the root directory where the data lies
        train='senti.train.tsv', 
        validation="senti.dev.tsv",
        test = "senti.test.tsv",
        format='tsv',
        fields=[("text", TEXT), ("label", LABEL)])

# 我们 使用TEXT field 构建字典

#MAX_VOCAB_SIZE = 14000
TEXT.build_vocab(train)
LABEL.build_vocab(train)


print(f"Unique tokens in TEXT vocabulary: {len(TEXT.vocab)}")
print(f"Unique tokens in LABEL vocabulary: {len(LABEL.vocab)}")

Unique tokens in TEXT vocabulary: 16284
Unique tokens in LABEL vocabulary: 3

# 接下来我们看下数据内容格式

print('TabularDataset 举例说明:')
example = val.examples[0]

print('text = ',example.text)
print('label = ',example.label)

print('*' * 60)
print('让我们看下字典数据：')
print('mapping(word->index)的映射关系: ',list(TEXT.vocab.stoi.items())[:5])
print('LABEL LABEL :',dict(LABEL.vocab.stoi))  # 这个感觉？？？
print('高词频数据topK:\n',TEXT.vocab.freqs.most_common(10))

TabularDataset 举例说明:
text =  ['It', "'s", 'a', 'charming', 'and', 'often', 'affecting', 'journey', '.']
label =  1
************************************************************
让我们看下字典数据：
mapping(word->index)的映射关系:  [('', 0), ('', 1), (',', 2), ('the', 3), ('and', 4)]
LABEL LABEL : {'': 0, '1': 1, '0': 2}
高词频数据topK:
 [(',', 25980), ('the', 24648), ('and', 19871), ('a', 19622), ('of', 17886), ('.', 12673), ('to', 12483), ("'s", 8764), ('is', 8638), ('that', 7689)]

创建数据集的Iterator

• 在训练时，我们使用一种特殊 Iterator，我们称为BucketIterator.来处理我们的数据

• 网络中进行训练，希望每个batch中的数据的长度一致

  例如： [ [3, 15, 2, 7], [4, 1], [5, 5, 6, 8, 1] ] -> [ [3, 15, 2, 7, 0], [4, 1, 0, 0, 0], [5, 5, 6, 8, 1] ]

  这里我们通过mask 来获取实际文本中单词内容，用于区分那个位置上的单词是padding的

• BucketIterator加载的数据的text 默认情况下[max_seq_length,batch_size] ,这里我们转换[batch_size,max_seq_length]

## 创建数据集的Iterator
from torchtext.data import Iterator, BucketIterator

BATCH_SIZE = 64
PAD_IDX = TEXT.vocab.stoi['']

train_iter, val_iter,test_iter = BucketIterator.splits(
        (train, val,test), # we pass in the datasets we want the iterator to draw data from
        batch_size=BATCH_SIZE, # 或者batch_sizes=(xx,xx,xx)
        device=device, # if you want to use the GPU, specify the GPU number here
        sort_key=lambda x: len(x.text), # the BucketIterator needs to be told what function it should use to group the data.
        sort_within_batch=True,
        repeat=False # we pass repeat=False because we want to wrap this Iterator layer.
)

我们来看下数据

val_data = next(iter(val_iter))
val_data

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x7]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]

inputs,lengths = val_data.text
targets = val_data.label
mask = 1 - (inputs == TEXT.vocab.stoi['']).float()
print("inputs: ",inputs.shape)
print("lengths: ",lengths.shape)
print("target: ",targets.shape)
print("pad_idx: ", TEXT.vocab.stoi[''])
print("mask = ",mask.shape)

inputs:  torch.Size([64, 7])
lengths:  torch.Size([64])
target:  torch.Size([64])
pad_idx:  1
mask =  torch.Size([64, 7])

print('train_iter: ')
for batch in train_iter:
    print(batch)
    break

print('val_iter: ')
for batch in val_iter:
    print(batch)
    break
print('test_iter: ')
for batch in test_iter:
    print(batch)
    break

train_iter: 

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x14]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]
val_iter: 

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x7]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]
test_iter: 

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x6]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]

我们看看数据text，label数据结构

Self Attention 机制模型

• 定义一种基于self attention的句子模型。

模型整体思路（实际 上 pytorch 中 transformer 的dot product 计算得分方案）：

单词t的权重是该单词的embedding和所有其他单词的embedding的dot product的和,然后 做sof t max归一化

当前单词与所有其它单词的dot product的和 $$a_{ts}=emb(x_t{)}^{T}emb(x_s)$$

softmax 归一化后的得分 $${\alpha }_t\propto \exp (\sum _s{a}_{ts})$$
x_t 是句子 x 中的第 t 个单词。我们使 用 emb 来表示单词的 embedding 函数

句子的向量表示： 单词t 加权求和后的向量 $$h_{self}=\sum _t{a}_{t}emb(x_t)$$

• 这个句子是正面情感的概率为:

$$\sigma (w^T{h}_{self})$$

• 可以在模型中加入residual connection，将输入的词向量平均向量加入进去

$$\sigma (w^T(h_{self}+h_{avg}))$$

模型定义

import math
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class SelfAttentionModel(nn.Module):
    
    def __init__(self,vocab_size,embedding_dim,p_drop,output_size,padding_idx,residual_conn=False):
        super(SelfAttentionModel,self).__init__()
        self.residual_conn = residual_conn
        self.drop = nn.Dropout(p_drop)
        self.embeddings = nn.Embedding(vocab_size,embedding_dim,padding_idx=padding_idx)
        self.linear = nn.Linear(embedding_dim,output_size)
        
        self.init_weights()
        # 增加-发现模型可以快速收敛到一个比较好的模型 （也可以不加尝试运行）
        # 参考官方文档： https://pytorch.org/tutorials/advanced/dynamic_quantization_tutorial.html
        
    def init_weights(self):
        initrange = 0.1
        self.embeddings.weight.data.uniform_(-initrange, initrange)
        self.linear.bias.data.zero_()
        self.linear.weight.data.uniform_(-initrange, initrange)
    

    def forward(self,inputs,mask):
        # inputs:[batch_size,seq_len]
        # mask: [batch_size,seq_len]
        # (batch_size, seq_len, embedding_dim)
        query = self.drop(self.embeddings(inputs))
        key = self.drop(self.embeddings(inputs))
        value = self.drop(self.embeddings(inputs))

        h_self,_=self.attention(query,key,value,mask=mask)
        
        if self.residual_conn:
            # 输入的词向量平均向量
            mask = mask.unsqueeze(2) #[batch_size,seq_len,1]
            query = query * mask #[batch_size,seq_len,embedding_dim] 对于padding的数据设置0
            h_avg = query.sum(1) / (mask.sum(1) + 1e-5) # 句子的平均的向量
            h_self = h_avg + h_self
            
        return self.linear(h_self).squeeze()
    
    
    def attention(self,query, key, value, mask=None, dropout=None):
  
        """
            Compute Scaled Dot Product Attention
            参考： http://nlp.seas.harvard.edu/2018/04/03/attention.html
            
            按照self attention计算公式实现模型定义
        """
        d_k = query.size(-1)
        
        # 这里的得分 参考transformer 实现，增加math.sqrt(d_k)
        scores = torch.matmul(query, key.transpose(-2, -1))/math.sqrt(d_k) #[batch_size,seq_len,seq_len]
        if mask is not None:
            mask= mask.unsqueeze(2)#[batch_size,seq_len,1]
            scores = scores.masked_fill(mask == 0, -1e9)
        # softmax 归一化后的得分        
        p_attn = F.softmax(scores, dim = -1)
        # 加权求和
        h_self = torch.matmul(p_attn, value).sum(1) # [batch_seq,embedding_size]
        
        return h_self,p_attn # 句子的向量、attention归一化后的得分
        
#
vocab_size = len(TEXT.vocab)
embedding_dim = 200
p_drop = 0.5
output_size = 1 
padding_idx = TEXT.vocab.stoi['']
model = SelfAttentionModel(vocab_size,embedding_dim,p_drop,output_size,padding_idx)
model = model.to(device)
#
optimizer = optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.BCEWithLogitsLoss() # BCEWithLogitsLoss : the sigmoid and the binary cross entropy 

print('train_iter: ')
for batch in train_iter:
    print(batch)
    print('*'*60)
    inputs,lengths = batch.text 
    targets = batch.label# [batch_size]
    mask = 1 - (inputs==TEXT.vocab.stoi['']).float()
    print("inputs:" ,inputs.shape) #[batch_size, max_seq_len]
    print("targets:",targets.shape)# [batch_size]
    print("mask:",mask.shape) #[batch_size, max_seq_len]
    preds = model.forward(inputs,mask)
    print(preds[0])
    break

train_iter: 

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x1]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]
************************************************************
inputs: torch.Size([64, 1])
targets: torch.Size([64])
mask: torch.Size([64, 1])
tensor(-0.0674, grad_fn=)

定义训练函数

• 直接计算attention的得分模型训练模型
• 计算attenttion得分，然后加上query的平均的hidden向量，然后训练模型

import time

def epoch_time(start_time, end_time):
    elapsed_time = end_time - start_time
    elapsed_mins = int(elapsed_time / 60)
    elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
    return elapsed_mins, elapsed_secs

def binary_accuracy(preds, y):
    """
    Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
    """

    #round predictions to the closest integer
    rounded_preds = torch.round(torch.sigmoid(preds))
    correct = (rounded_preds == y).float() #convert into float for division 
    acc = correct.sum() / len(correct)
    return acc

def train(model,train_iter,criterion,optimizer):
    
    epoch_acc = 0.
    epoch_loss = 0.
    model.train()

    for batch in train_iter:
        #
        inputs,lengths = batch.text 
        targets = batch.label# [batch_size]
        mask = 1 - (inputs==TEXT.vocab.stoi['']).float()

        preds = model(inputs,mask)

        #
        loss = criterion(preds,targets) # BCEWithLogitsLoss 计算这个batch的平均loss
        acc = binary_accuracy(preds, targets) # 计算这个batch的平均的准确率
        epoch_acc += acc.item()  # 当前批次准确率
        epoch_loss += loss.item()  # 当前批次loss
        # 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    return epoch_acc / len(train_iter),epoch_loss / len(train_iter) # 对所有批次求平均= 平均的acc和loss

def evaluate(model,data_iter,criterion):
   
    epoch_acc = 0.
    epoch_loss = 0.

    model.eval()
    with torch.no_grad():
        for batch in data_iter:
            #
            inputs,lengths = batch.text 
            targets = batch.label# [batch_size]
            mask = 1 - (inputs==TEXT.vocab.stoi['']).float()
            preds = model(inputs,mask)

            #
            loss = criterion(preds,targets)
            acc = binary_accuracy(preds, targets)
            epoch_acc += acc.item()
            epoch_loss += loss.item()

    return epoch_acc / len(data_iter),epoch_loss / len(data_iter)

模型训练

vocab_size = len(TEXT.vocab)
embedding_dim = 200
p_drop = 0.5
output_size = 1 
padding_idx = TEXT.vocab.stoi['']
model = SelfAttentionModel(vocab_size,embedding_dim,p_drop,output_size,padding_idx)
model = model.to(device)
#
optimizer = optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.BCEWithLogitsLoss() # BCEWithLogitsLoss : the sigmoid and the binary cross entropy 

#
N_EPOCHS = 5
best_valid_loss = float('inf')
best_valid_acc = float('-inf')

for epoch in range(N_EPOCHS):

    start_time = time.time()

    train_acc,train_loss = train(model,train_iter,criterion,optimizer)
    val_acc,val_loss = evaluate(model,val_iter,criterion)

    end_time = time.time()

    epoch_mins, epoch_secs = epoch_time(start_time, end_time)

    if val_acc > best_valid_acc:
        print('val acc creasing->')
        best_valid_acc = val_acc
        torch.save(model.state_dict(), 'self_attention-model.pt')
        
    print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
    print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
    print(f'\t Val. Loss: {val_loss:.3f} |  Val. Acc: {val_acc*100:.2f}%')
    
    
model.load_state_dict(torch.load('self_attention-model.pt'))
test_acc,test_loss = evaluate(model,test_iter,criterion)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')

val acc creasing->
Epoch: 01 | Epoch Time: 0m 52s
	Train Loss: 0.384 | Train Acc: 83.46%
	 Val. Loss: 0.563 |  Val. Acc: 80.09%
val acc creasing->
Epoch: 02 | Epoch Time: 1m 0s
	Train Loss: 0.227 | Train Acc: 91.40%
	 Val. Loss: 0.682 |  Val. Acc: 80.18%
Epoch: 03 | Epoch Time: 1m 1s
	Train Loss: 0.190 | Train Acc: 92.84%
	 Val. Loss: 0.738 |  Val. Acc: 79.87%
val acc creasing->
Epoch: 04 | Epoch Time: 1m 2s
	Train Loss: 0.170 | Train Acc: 93.62%
	 Val. Loss: 0.799 |  Val. Acc: 81.18%
val acc creasing->
Epoch: 05 | Epoch Time: 1m 3s
	Train Loss: 0.157 | Train Acc: 94.27%
	 Val. Loss: 0.846 |  Val. Acc: 81.41%
Test Loss: 0.754 | Test Acc: 80.42%

设置 residual_conn=True 重新训练模型

vocab_size = len(TEXT.vocab)
embedding_dim = 200
p_drop = 0.5
output_size = 1 
padding_idx = TEXT.vocab.stoi['']
model = SelfAttentionModel(vocab_size,embedding_dim,p_drop,output_size,padding_idx,residual_conn=True)
model = model.to(device)
#
optimizer = optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.BCEWithLogitsLoss() # BCEWithLogitsLoss : the sigmoid and the binary cross entropy 

#
N_EPOCHS = 5
best_valid_loss = float('inf')
best_valid_acc = float('-inf')

for epoch in range(N_EPOCHS):

    start_time = time.time()

    train_acc,train_loss = train(model,train_iter,criterion,optimizer)
    val_acc,val_loss = evaluate(model,val_iter,criterion)

    end_time = time.time()

    epoch_mins, epoch_secs = epoch_time(start_time, end_time)

    if val_acc > best_valid_acc:
        print('val acc creasing->')
        best_valid_acc = val_acc
        torch.save(model.state_dict(), 'self_attention-model.pt')
        
    print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
    print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
    print(f'\t Val. Loss: {val_loss:.3f} |  Val. Acc: {val_acc*100:.2f}%')
    
    
model.load_state_dict(torch.load('self_attention-model.pt'))
test_acc,test_loss = evaluate(model,test_iter,criterion)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')

val acc creasing->
Epoch: 01 | Epoch Time: 1m 0s
	Train Loss: 0.363 | Train Acc: 84.31%
	 Val. Loss: 0.529 |  Val. Acc: 80.31%
Epoch: 02 | Epoch Time: 1m 12s
	Train Loss: 0.210 | Train Acc: 91.88%
	 Val. Loss: 0.632 |  Val. Acc: 80.16%
Epoch: 03 | Epoch Time: 1m 13s
	Train Loss: 0.177 | Train Acc: 93.31%
	 Val. Loss: 0.664 |  Val. Acc: 80.29%
val acc creasing->
Epoch: 04 | Epoch Time: 1m 8s
	Train Loss: 0.158 | Train Acc: 94.10%
	 Val. Loss: 0.757 |  Val. Acc: 80.51%
Epoch: 05 | Epoch Time: 1m 18s
	Train Loss: 0.146 | Train Acc: 94.53%
	 Val. Loss: 0.812 |  Val. Acc: 79.44%
Test Loss: 0.714 | Test Acc: 79.56%

发现效果并没有变好

在线预测

tokenizer = lambda x: x.split()
def predict_sentiment(model, text):
    
    model.eval()
    indexed = torch.LongTensor([TEXT.vocab.stoi.get(t, PAD_IDX) for t in tokenizer(text)]).to(device)
    indexed = indexed.unsqueeze(0) #[batch_size,seq_len]
    mask = 1 - (indexed == TEXT.vocab.stoi['']).float()
    with torch.no_grad():
        pred = torch.sigmoid(model(indexed, mask)) # sigmoid(wx + b) ,最终返回结果概率
    return pred.item()

predict_sentiment(model,"hide new secretions from the parental units")

0.006493980064988136

predict_sentiment(model,"Uneasy mishmash of styles and genres")

0.010009794495999813

predict_sentiment(model,'Director Rob Marshall went out gunning to make a great one .')

0.9782317280769348

predict_sentiment(model,'A well-made and often lovely depiction of the mysteries of friendship .')

0.9999963045120239

设计Attention函数模型训练

为提供情感分类的模型效果，我们加入了attention 机制。 那么接下来我们自己设计一个Attention函数，一般思路如下：

• 研究dot product 和cosine similarity在attention机制上的区别（前面章节已经代码实现）
• 使用transformation来区分key, query和value
• 使用多个Attention heads
• 使用positional encodings来增加单词的位置信息
• 更多思路。。。

可以参考如下代码

Transformer的模型, 参考资料如下：

• The Annotated Transformer

transformer 模型架构

Embeddings and Softmax

Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension $d_{\text{model}}$. We also use the usual learned linear transformation and softmax function to convert the decoder output to predicted next-token probabilities. In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation, similar to (cite). In the embedding layers, we multiply those weights by $\sqrt{d_{\text{model}}}$.

class InputEmbeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(InputEmbeddings, self).__init__()
        self.embed = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.embed(x) * math.sqrt(self.d_model)

Positional Encoding

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{\text{model}}$ as the embeddings, so that the two can be summed. There are many choices of positional encodings, learned and fixed (cite).

In this work, we use sine and cosine functions of different frequencies:
$$P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{\text{model}}})$$

$$P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{\text{model}}})$$
where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000\cdot 2\pi$. We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $P{E}_{pos+k}$ can be represented as a linear function of $P{E}_{pos}$.

In addition, we apply dropout to the sums of the embeddings and the positional encodings in both the encoder and decoder stacks. For the base model, we use a rate of $P_{drop}=0.1$.

import torch
from torch.autograd import Variable

class PositionalEncoding(nn.Module):
    '''
        Implement the PE function.
        
    '''
        
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        
        # CPU下稍微修改下  https://blog.csdn.net/brandday/article/details/100518612
        position = torch.arange(0., max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0., d_model, 2) *
                             -(math.log(10000.0) / d_model))
        
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], 
                         requires_grad=False)
        return self.dropout(x)

Below the positional encoding will add in a sine wave based on position. The frequency and offset of the wave is different for each dimension.

torch.zeros(1, 100, 20).shape

torch.Size([1, 100, 20])

import matplotlib.pyplot as plt
%matplotlib inline

plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)# d_model = 20,dropout=0

y = pe.forward(Variable(torch.zeros(1, 100, 20)))
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
g=plt.legend(["dim %d"%p for p in [4,5,6,7]])

Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

We call our particular attention “Scaled Dot-Product Attention”. The input consists of queries and keys of dimension $d_k$, and values of dimension $d_v$. We compute the dot products of the query with all keys, divide each by $\sqrt{d_k}$, and apply a softmax function to obtain the weights on the values.

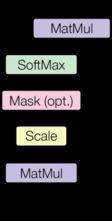
In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix $Q$. The keys and values are also packed together into matrices $K$ and $V$. We compute the matrix of outputs as:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

Multi-head attention

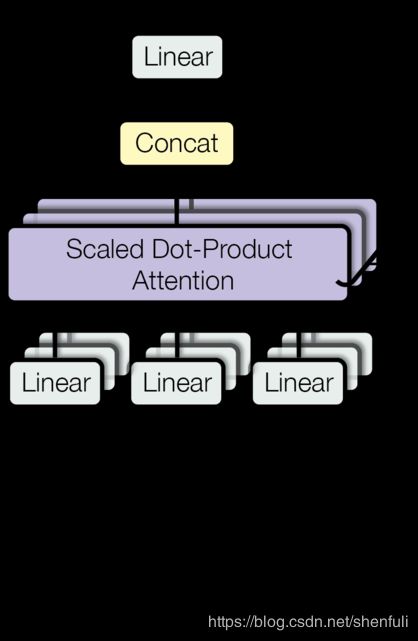
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.
$$\begin{gathered} \mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}(Q,K,V)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_1,...,\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_{\mathrm{h}})W^O \\ \text{where}\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_{\mathrm{i}}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V) \end{gathered}$$

Where the projections are parameter matrices $W_i^Q\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{\text{model}}\times d_v}$ and $W^O\in {\mathbb{R}}^{h{d}_v\times d_{\text{model}}}$. In this work we employ $h=8$ parallel attention layers, or heads. For each of these we use $d_k=d_v=d_{\text{model}}/h=64$. Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

import copy

import torch
import torch.nn as nn
def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
    
    
def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)

import math
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class MyTransformerModel(nn.Module):
    
    def __init__(self,vocab_size,d_model,p_drop,h,output_size):
        super(MyTransformerModel,self).__init__()
        self.drop = nn.Dropout(p_drop)
              
        self.embeddings = InputEmbeddings(d_model,vocab_size)
        self.position = PositionalEncoding(d_model, p_drop)
        self.attn = MultiHeadedAttention(h, d_model) 
        self.norm = nn.LayerNorm(d_model)
        self.linear = nn.Linear(d_model, output_size)
        self.init_weights()
        # 增加-发现模型可以快速收敛到一个比较好的模型 （也可以不加尝试运行）
        # 参考官方文档： https://pytorch.org/tutorials/advanced/dynamic_quantization_tutorial.html
        
       
    def init_weights(self):
        initrange = 0.1
        self.linear.bias.data.zero_()
        self.linear.weight.data.uniform_(-initrange, initrange)
    

    def forward(self,inputs,mask):
        
        # 1. embed
        # (batch_size, seq_len, d_model)
        embeded = self.embeddings(inputs) 
        
        # 2. postional
        # (batch_size, seq_len, d_model)
        embeded = self.position(embeded)
        
        # (batch_size,seq_len,1)
        mask = mask.unsqueeze(2)
        
        # 3. multi header
        # (batch_size, seq_len, d_model)
        inp_attn = self.attn(embeded,embeded,embeded,mask)
        inp_attn = self.norm(inp_attn + embeded)
        
        # 4. linear
        # (batch_size, seq_len, d_model)
        inp_attn = inp_attn * mask 
        
        #(batch_size,d_model)
        h_avg = inp_attn.sum(1)/(mask.sum(1) + 1e-5)  
        
        return self.linear(h_avg).squeeze()
        
    
vocab_size = len(TEXT.vocab)
print('vocab_size : ',vocab_size)
d_model = 512
p_drop = 0.5
h=2
output_size=1
model = MyTransformerModel(vocab_size,d_model,p_drop,h,output_size)
model = model.to(device)
#
optimizer = optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.BCEWithLogitsLoss() # BCEWithLogitsLoss : the sigmoid and the binary cross entropy 

print('train_iter: ')
for batch in train_iter:
    print(batch)
    print('*'*60)
    inputs,lengths = batch.text 
    targets = batch.label# [batch_size]
    mask = 1 - (inputs==TEXT.vocab.stoi['']).float()
    print("inputs:" ,inputs.shape) #[batch_size, max_seq_len]
    print("targets:",targets.shape)# [batch_size]
    print("mask:",mask.shape) #[batch_size, max_seq_len]
    preds = model.forward(inputs,mask)
    break

vocab_size :  16284
train_iter: 

[torchtext.data.batch.Batch of size 64]
	[.text]:('[torch.LongTensor of size 64x9]', '[torch.LongTensor of size 64]')
	[.label]:[torch.FloatTensor of size 64]
************************************************************
inputs: torch.Size([64, 9])
targets: torch.Size([64])
mask: torch.Size([64, 9])

模型训练

vocab_size = len(TEXT.vocab)
print('vocab_size : ',vocab_size)
d_model = 512
p_drop = 0.5
h=4
output_size=1
model = MyTransformerModel(vocab_size,d_model,p_drop,h,output_size)
model = model.to(device)
#
optimizer = optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.BCEWithLogitsLoss() # BCEWithLogitsLoss : the sigmoid and the binary cross entropy 

#
N_EPOCHS = 5
best_valid_acc = float('-inf')

for epoch in range(N_EPOCHS):

    start_time = time.time()

    train_acc,train_loss = train(model,train_iter,criterion,optimizer)
    val_acc,val_loss = evaluate(model,val_iter,criterion)

    end_time = time.time()

    epoch_mins, epoch_secs = epoch_time(start_time, end_time)

    if val_acc > best_valid_acc:
        print('val acc creasing->')
        best_valid_acc = val_acc
        torch.save(model.state_dict(), 'mytransformer-model.pt')
        
    print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
    print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
    print(f'\t Val. Loss: {val_loss:.3f} |  Val. Acc: {val_acc*100:.2f}%')
    
    
model.load_state_dict(torch.load('mytransformer-model.pt'))
test_acc,test_loss = evaluate(model,test_iter,criterion)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')

vocab_size :  16284
val acc creasing->
Epoch: 01 | Epoch Time: 2m 41s
	Train Loss: 0.613 | Train Acc: 68.19%
	 Val. Loss: 0.515 |  Val. Acc: 75.54%
val acc creasing->
Epoch: 02 | Epoch Time: 3m 9s
	Train Loss: 0.446 | Train Acc: 81.84%
	 Val. Loss: 0.452 |  Val. Acc: 79.29%
val acc creasing->
Epoch: 03 | Epoch Time: 3m 24s
	Train Loss: 0.360 | Train Acc: 86.49%
	 Val. Loss: 0.444 |  Val. Acc: 79.64%
val acc creasing->
Epoch: 04 | Epoch Time: 3m 22s
	Train Loss: 0.315 | Train Acc: 88.59%
	 Val. Loss: 0.430 |  Val. Acc: 81.50%
val acc creasing->
Epoch: 05 | Epoch Time: 3m 24s
	Train Loss: 0.280 | Train Acc: 89.83%
	 Val. Loss: 0.422 |  Val. Acc: 81.90%
Test Loss: 0.420 | Test Acc: 81.02%

loss 和 val acc 可以加大训练，效果可能会更好，这里就不继续实验了