深圳二手房房价分析与建模预测(附数据集)
之前帮师兄做了一个预测房价课题的demo,但是感觉效果不好,考虑到当时数据来源是长沙的房价数据,这次决定自己收集深圳的二手房数据来建模预测。
原本是准备上网找现成的数据集,结果很多github上的代码接口都失效了,考虑到房价的时效性,决定自食其力自己动手爬取用scrapy框架爬取。
目标是安居客网站,字段包含楼盘名、楼盘建造时间、粗略位置、房屋类型、产权年限、户型、面积、朝向、楼层、有无电梯、均价、总价、是否一手房、装修程度等14个字段。
没有太严苛的反爬虫手段,很快把整个网站爬遍了,也只汇集了大概6000多条项目如下图:

分析主要所用到的库为numpy、pandas、scipy、matplotlib、seaborn、sklearn等
首先在项目文件下倒入文件(我习惯保存数据副本到本地)
然后就是数据清洗。
先看看缺失值
df = pd.read_csv("anjuke.csv")
print(df.info())
print(df.describe())

没有任何缺失值,说明房子信息的录入比较完整。
接下来就是异常值了
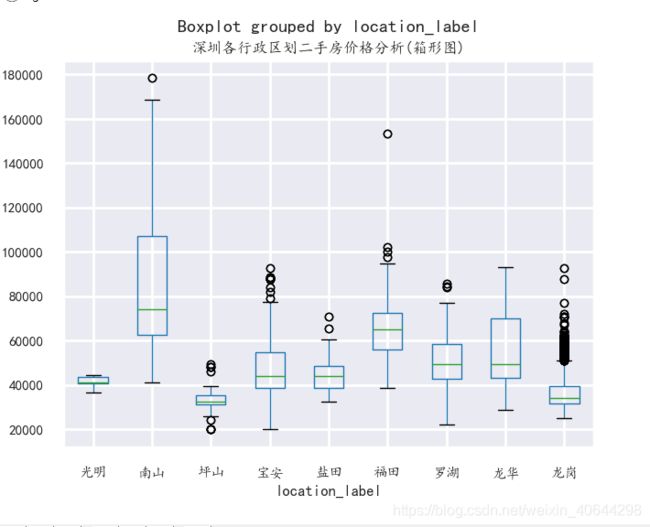
首先先用箱线图直观的描绘价格(指均指)的分布情况。
如图
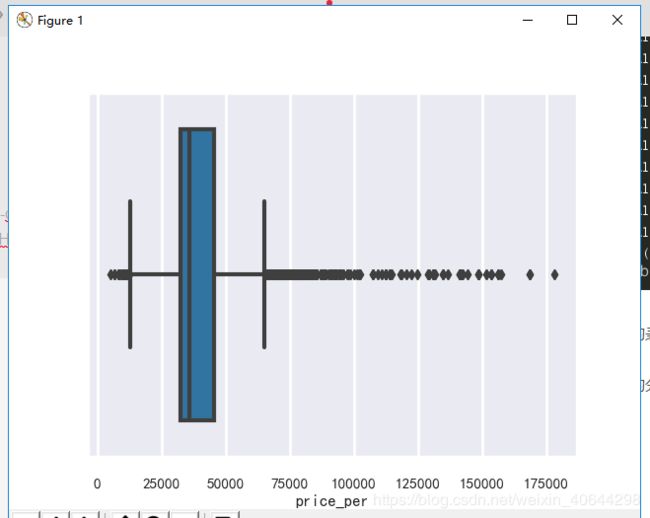
可以看出来偏态肯定是偏大的,其实有偏高的异常值我倒不觉得奇怪,毕竟这是真实的数据反映,现实就是如此(三四十万一平的房子深圳有的是)。但是看到深圳有房子每平均价低于1w的房子,这肯定不可能,于是我打开链接仔细的看看,发现猫腻在这
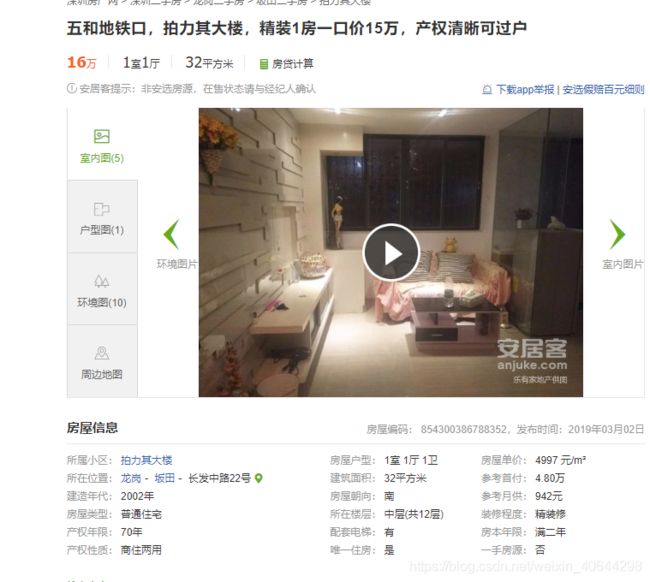

果不其然是小产权房
这些数据暂时不在考虑范围,结合深圳的商品房的房价实际,我去掉了所有房价低于两万的房子
print(df.info())
print(df.describe())
sns.boxplot(df['price_per'])
plt.show()
a=df.loc[df['price_per']<20000].index#去除均价20000以下的项
df=df.drop(index=a,axis=0)
然后看看字段,发现产权栏几乎都是70年,没有什么意义。而户型种类偏多,无法进行后续的定序,也没有太大的价值,而总价一项就是均价乘以面积,信息冗余,也整列删除。
df=df.drop(['Huxin',"type","Chanquan","price_sum"],axis=1)
其实我也考虑过把朝向给删掉,但是我对朝向进行groupby汇总时发现不同的朝向的房子均价还是有很大的差异的,如朝东西的房子均价远高于朝南的房子(原谅我没买过房我也不知道为什么,不是说坐北朝南吗?),所以该列得到保留。
zx = {'毛坯':1,'简单装修':2,'精装修':3,'豪华装修':4}
df['zx_level_num']=df['zx_level'].map(zx)
print(df["zx_level"])
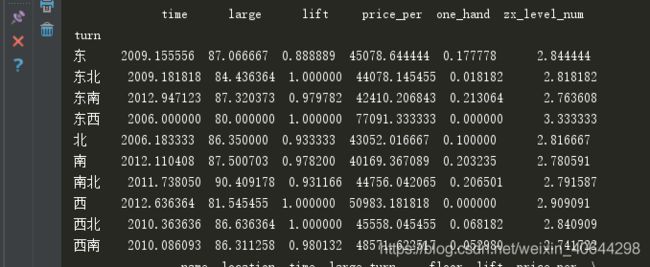
print(df.groupby('turn').mean())
turn = {'东':1,'东北':2,'东西':3,'东南':4,'北':5,'南':6,'南北':7,'西':8,'西北':9,'西南':10}
df['turn_num']=df['turn'].map(turn)
因为在爬却的时候已经去重过了,所以在这里不必进行数据去重。
还有就是对楼层高低的变量数字定序
由于楼层的数据都是
直接用正则化提取中高低,并且转换为数字离散变量
for i in df['floor']:
a=re.search("([\u4e00-\u9fa5]{1}).*",i).group(1)
if a=="低":
a=0
elif a=="中":
a=1
else:
a=2
s.append(a)
df['floor_num']=s
而地理位置因为都是如“南山-南油”、“龙岗-坂田”此类,如果将“南山-南油”和“南山-南头”分看看成两个类别,一会失去整体性,二是考虑到数据集本来就不多,于是进行以下变换
sls=[]
for i in df['location']:
a=re.search("([\u4e00-\u9fa5]{2}).*",i).group(1)
sls.append(a)
df["location_label"]=sls
location_num = {"坪山":1,"龙岗":2,"光明":3,"盐田":4,"宝安":5,"罗湖":6,"龙华":7,"福田":8,"南山":9}
df["location_num"] = df["location_label"].map(location_num)
其中还发现残留了一些地点值为“深圳周边”的项目,一同删掉
先以地址为分组,求均值得到
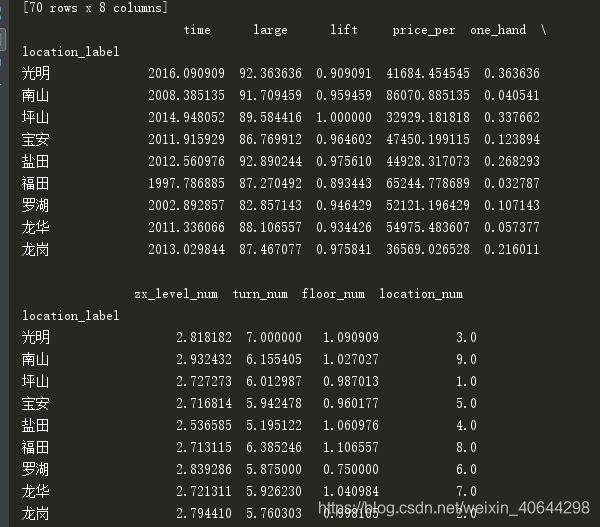
南山的二手房均价比坪山和龙岗加起来还多,这样算起来我的宿舍价值不菲(感谢学校)
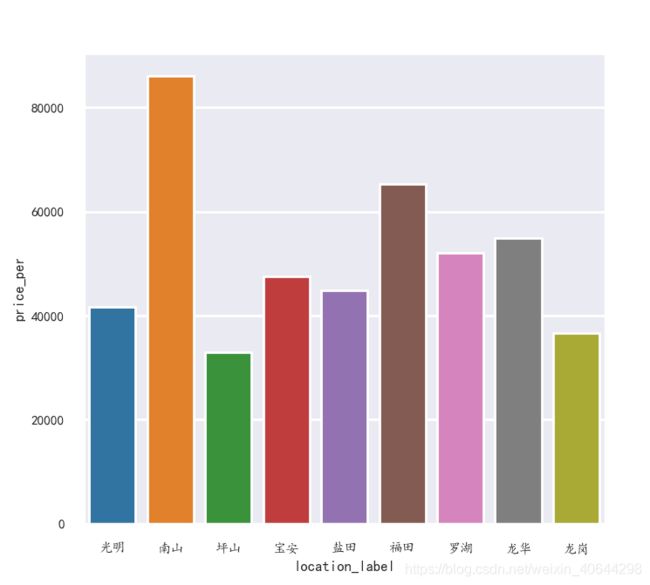
这样看可能不够直观,利用图表
来看总的图表
a = df.groupby("location_label").mean()#df.groupby()
sns.barplot(a.index,a["price_per"])
labs = df["location_label"].value_counts().index
explodes=[0.1 if i=="龙岗" else 0 for i in labs]
plt.pie(df["location_label"].value_counts(normalize=True),labels=labs,explode=explodes,autopct="%1.1f%%",colors=sns.color_palette("Reds"))
plt.show()
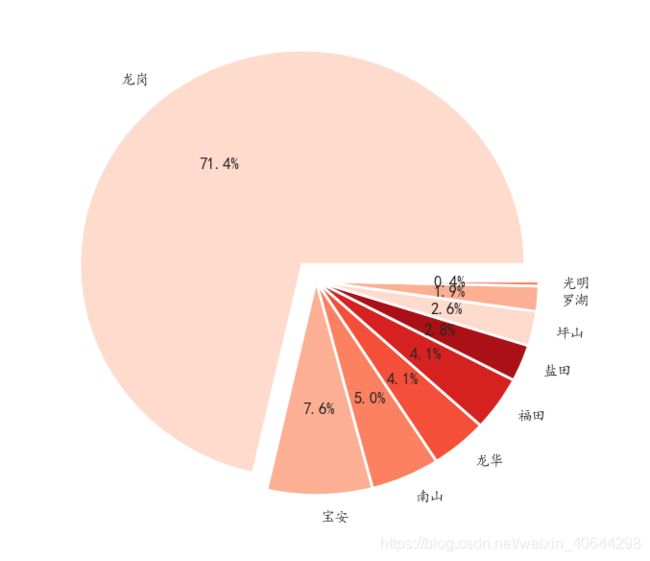
虽然龙岗是深圳最大的区,但是这样的数据分布肯定是不均衡的,需要在建立模型前对特定的数据进行过抽样或者欠抽样。
这个数据也确实反映了龙岗的二手房数量大,区域性人口流动量大。而且由于数量大,更容易凸显出二手房价的异常值。
相关性分析(pearson系数)
print(df.groupby('location_label').mean())
print(df.corr())
print(df.std())#显示离中趋势
print(df.var())#方差
print(df.skew())#偏态系数
print(df.kurt())#峰态系数
sns.heatmap(df.corr())
plt.show()

看图比较直接
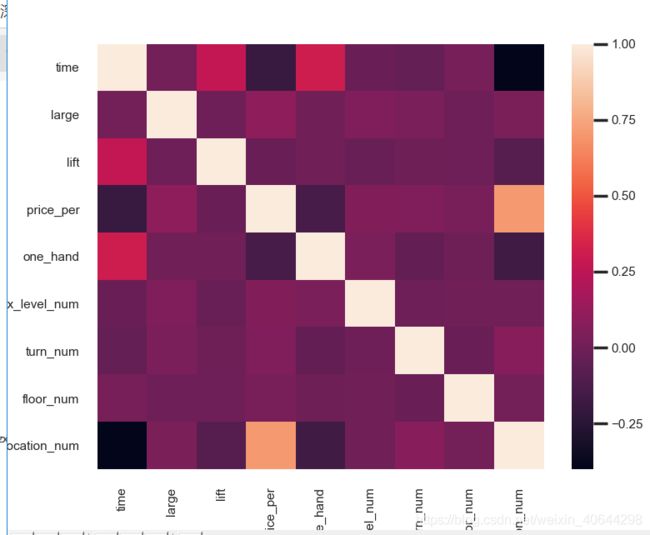
其中颜色越浅表示正相关、颜色越深(接近黑色)就是呈负相关。
明显房子均价与地理位置呈强正相关,而房子均价与楼盘时间和是否一手房呈弱负相关。
这一开始让我奇怪,仔细想想也没有错,因为在深圳建的越早的房子,往往地理位置特别好、尤其像罗湖这样的老地段、而这种房子交通方便、还很有可能带学位等等,而年代越久的房子,也更加不可能是一手房。从下图可以看的出来时间较长的楼盘多数在关内。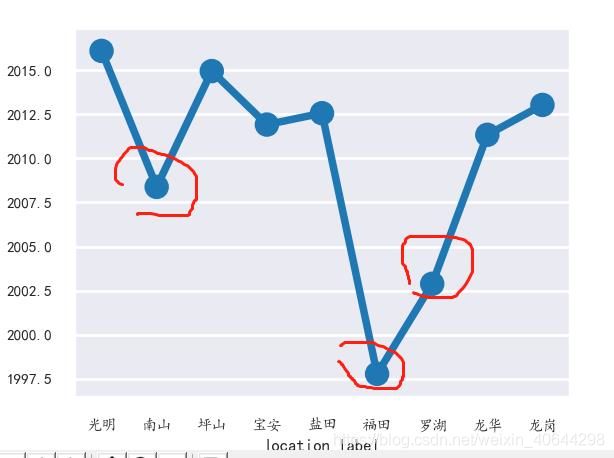
与此同时年份与房屋面积也有一定的相关趋势,
而各个区的房屋和面积对房价的影响经过简单的线性拟合后可得如下图
def plot_line():
plt.figure(figsize=(5,4),dpi=128)
colors = [ 'red', 'red',
'blue', 'blue',
'green', 'green',
'gray', 'gray', 'gray']
district = ["坪山","龙岗","光明","盐田","宝安","罗湖","龙华","福田","南山"]
markers = ['o','s',
'o', 's',
'o', 's',
'o', 's', 'v']
for i in range(9):
x = df.loc[df['location_label'] == district[i]]['large']
y = df.loc[df['location_label'] == district[i]]['price_per']
A, B = optimize.curve_fit(linearfitting, x, y)[0]
xx = np.arange(0, 2000, 100)
yy = A * xx + B
plt.plot(xx, yy, c=colors[i], marker=markers[i],label=district[i],linewidth=1)
plt.legend(loc=1,bbox_to_anchor=(1.138,1.0),fontsize=10)
plt.xlim(0,500)
plt.ylim(0,180000)
plt.title('深圳各行政区内房屋面积对房价的影响(线性拟合)',fontsize=10)
plt.xlabel('房屋面积(平方米)',fontsize=8)
plt.ylabel('房屋单价(元/平方米)',fontsize=8)
plt.show()
plot_line()
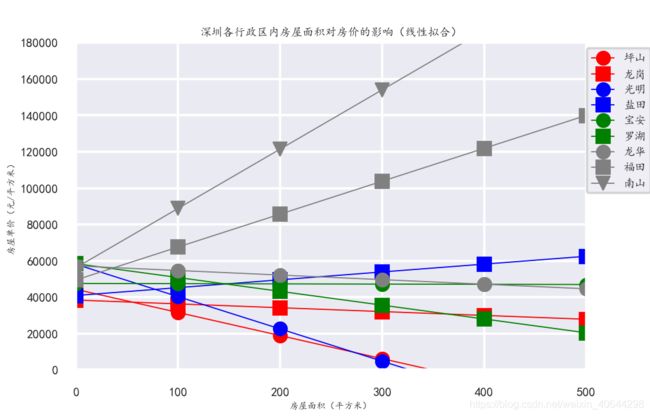
当然这只是一个简单假设的线性趋势,不能作为真实参考,光明的三百平米的房子不可能均价为零,现实生活绝大多数场景都是非线性的。
而房子平均室内面积随着年份也趋于稳定如下图(房价升高,平均房子面积会缩水,香港人称90平米的房子叫千尺豪宅)。
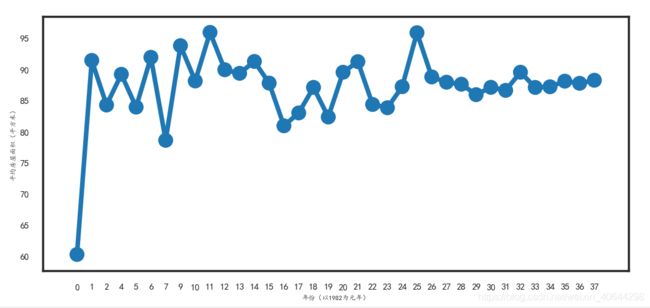
在建模之前,对字段“location”中龙岗的字段进行简单欠采样,对其他的数据进行随机过采样。将位置中属于龙岗的项目数量降到了总体的百分之五十。
在训练前,对不同地区进行等比率抽样,提取出500数据作为额外预测。对数据进行特征标准化,考虑到年份的波动相对于其基数过小、将全部年份减去最低年份(1982)。将剩下的数据进行三折交叉验证,利用r2_score作为评价函数,取平均准确度作为最终的结果。鉴于特征数量少,没有必要进行降维。
参与的模型包括线性回归、lasso、岭回归、随机森林、GradientBoostingRegressor、SVR(核函数为Gaussian radial basis function (RBF))等。
class Model():
def __init__(self,df):
self.df=df
self.model=(Lasso(),Ridge(alpha=.5),LinearRegression(),RandomForestRegressor(),GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
max_depth=1, random_state=0, loss='ls'),SVR(kernel="rbf"))
def pre_data(self):#特征标准化
m_s=preprocessing.MinMaxScaler().fit(self.df[features])
d_m=m_s.transform(self.df[features])
return d_m
def train_and_test(self):
data=self.pre_data()
#print(data)
kf=KFold(n_splits=3,shuffle=False,random_state=None)#设定
for a in self.model:
b=a
c=0
for train_index, test_index in kf.split(data):
#print('train_index', train_index, 'test_index', test_index)
feature_data=(data[train_index,:])#选定被训练的值
#print(feature_data)
predictions_data=(self.df[target].iloc[train_index])
#print(predictions_data)
b.fit(feature_data,predictions_data)#训练
pred_result=b.predict(data[test_index,:])
pred_result2=b.predict(self.pre_data())
c+=r2_score(self.df[target].iloc[test_index],pred_result)
print(c/3)
结果线性回归、lasso、岭回归的R2值仅在0.5左右,svr为0.7,
集成学习中随机森林0.9
最后梯度提升树(GBDT)以R2均值=0.93获胜
集成学习集体获得胜利。
来看看模型输出与预测与实际的曲线
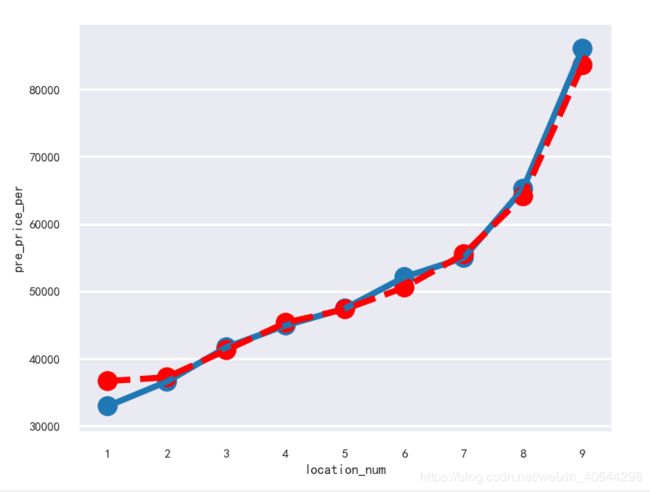
绝对有过拟合嫌疑,对其进行简单的调参修改(主要是步长和迭代最大次数)后,得到在未测试过的抽样数据集的测试结果曲线如下图。(红色是预估值)
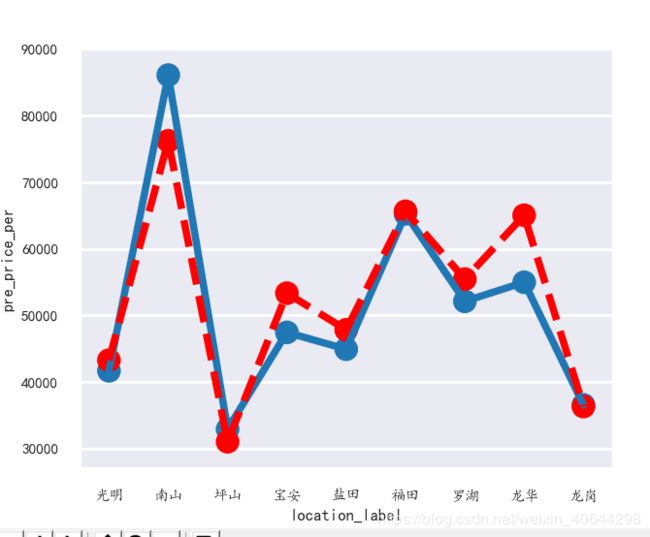
测试的R2均值为0.71,算是勉强经受住了考验,考虑到样本的数量偏少,而且现实中也有很多因素无法考虑,如是附近有没有交通设施、有没有商圈、绿化等等。且损失(合并)了一部分详细的地理信息,效果不算特别准确也是意料中的,多进行调参和适当的减枝,模型应该还有提升空间。
整个分析过程按部就班进行得特别快,但是完成后不由感叹深圳房子的负担却是会压跨不少人。深南大道上耸立了不少牌子说,来了就是深圳人,但依我看
能留下来的才是深圳人。
ps:数据集链接
password:kjkm