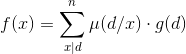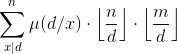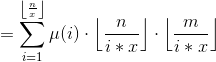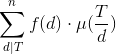莫比乌斯反演详解
莫比乌斯反演的基本思想
考虑求函数![]() ,我们可以构造一个比较好求函数g(x)使
,我们可以构造一个比较好求函数g(x)使 ,然后用g(x)来求f(x)
,然后用g(x)来求f(x)
怎么用g(x)来表示f(x)呢?
稍微列举一下g(x):
g(1)=f(1)
g(2)=f(1)+f(2)
g(3)=f(1)+f(3)
g(4)=f(1)+f(2)+f(4)
g(5)=f(1)+f(5)
g(6)=f(1)+f(2)+f(3)+f(6)
我们经过一番拼凑发现:
f(1)=g(1)
f(2)=(f(1)+f(2))-f(1)=g(2)-g(1)
f(3)=g(3)-g(1)
f(4)=(f(1)+f(2)+f(4))-(f(1)+f(2))=g(4)-g(2)
f(5)=g(5)-g(1)
f(6)=(f(1)+f(2)+f(3)+f(6))-(f(1)+f(3))-(f(1)+f(2))+f(1)=g(6)-g(3)-g(2)+g(1)
在用g(x)表示f(x)时,我们进行了一些加加减减的操作。
感觉有点像容斥原理。。。
于是我们想要求出这个容斥原理的系数:
但是用瞪眼法观察了很久都一无所获
所以我们来理性分析一下:
对于每一个g(n),它都包含了它的 所有因子x 的f(x)之和,
但是我们只需要f(n)
所以我们需要减掉那些无关的f(x)
如:g(8)-g(4)=f(8)+f(4)+f(2)+f(1)-f(4)-f(2)-f(1) =f(8)
于是就出现了一个奇妙的想法:把n的所有因子的系数补全!
f(6)=1*g(6)+(-1)*g(3)+(-1)*g(2)+1*g(1)
f(8)=1*g(8)+(-1)*g(4)+0*g(2)+0*g(1)
f(12)=1*g(12)+(-1)*g(6)+(-1)*g(4)+0*g(3)+1*g(2)+0*g(1)
然后继续用瞪眼法分析。。。
发现g(x)前面的系数与x无关(因为g(1)前面的系数一会儿是1,一会儿是0)
g(x)前面的系数好像是与n/x有关
例如当n/x=1时,g(x)前面的系数总是1
当n/x=2时,g(x)前面的系数总是-1
当n/x=3时,g(x)前面的系数也总是-1
似乎对于每一个n/x,g(x)前的系数都是固定的。
所以我们猜想这个系数是一个关于n/x的函数。
而这个函数就是大名鼎鼎的莫比乌斯函数![]() !!!
!!!
既然容斥系数已经确定了,那么莫比乌斯定理也可以很轻松地表示出来了
当一个函数g(x)满足
那么
这个公式叫莫比乌斯约数反演
这个定理还有另一种形式(当然叫莫比乌斯倍数反演啦)(其实一般都用这种形式)
当一个函数g(x)满足
则
有了这两个公式,就可以进行一些神奇的操作啦
比如说给定n,m,求:
其中[gcd(i,j)==x]表示当gcd(i,j)=x时返回1,否则返回0
要求时间复杂度为O(n)
按照上面的第二个公式,我们构造一个函数g(x)满足:
反演一波:
仿佛并没有什么用的样子。。。
那先来看一下“所谓”好求的g(x)
可以发现gcd(i,j)是x的倍数时(因为d只能是x的倍数,所以gcd(i,j)也是x的倍数),才会对g(x)造成贡献
所以,g(x)可以简化为
我们设g=gcd(i,j),i=g*a,j=g*b
我们在改变a,b的值时gcd(i,j)也会改变但始终是x的倍数(因为i,j至少都有一个因子g)
所以,我们只需要取完a,b的所有的值就可以求出g(x)啦
很明显a能取的值有![]() 种,b能取的值有
种,b能取的值有![]() 种
种
再把g(x)带进去
很明显可以O(n)做了
其实,莫比乌斯反演的思想,
就是把一个很复杂的函数f(x),
转换为另一个很好求的函数g(x)
然后用g(x)来表示f(x),
从而降低时间复杂度
关于莫比乌斯反演的几个技巧
1、分块优化(也叫数论分块、整除分块)
由于![]() 只有
只有![]() 种取值,
种取值,
如:n=8
i=1,2,3,4,5,6,7,8
![]() =8,4,2,2,1,1,1,1
=8,4,2,2,1,1,1,1
于是我们枚举这![]() 种取值(从枚举定义域转到枚举值域也是一种重要思想),
种取值(从枚举定义域转到枚举值域也是一种重要思想),
对于每一种取值,只会有一个对应的f值
所以
i表示该段取值的起始点,last表示段取值的终点。
再来一个复杂一点的:
d的取值只有![]() 种,设i=d/x,则d=i*x
种,设i=d/x,则d=i*x
![]()
i=last+1
代码:(其中mu需要处理前缀和)
long long solve(int n,int m,int k)
{
if(n>m) swap(n,m);
if(!n||!m||!k) return 0;
n/=k;m/=k;
LL ans=0;
int last,i;
for(i=1;i<=n;i=last+1){
last=min(n/(n/i),m/(m/i));
ans=1ll*ans+1ll*(n/i)*(m/i)*(mu[last]-mu[i-1]);
}
return ans;
}
2、线性筛积性函数
实际上,类似于找规律(当然也可以硬推式子),只要你记住
每一个数只会被它的最小质因子筛掉
然后就可以找规律了。。。
有时候可以存一下必要的信息
线筛mu:
void shai()
{
mu[1]=1;vis[1]=1;
int i,j;
for(i=2;i<=N;i++){
if(!vis[i]){
prime[++tot]=i;
mu[i]=-1;
}
for(j=1;j<=tot;j++){
LL tmp=1ll*i*prime[j];
if(tmp>N) break;
vis[tmp]=1;
if(i%prime[j]==0){
mu[tmp]=0;
break;
}
else mu[tmp]=-mu[i];
}
}
}线筛phi:
void shai()
{
vis[1]=1;phi[1]=1;
int i,j;
for(i=2;i<=N;i++){
if(!vis[i]){
prime[++tot]=i;
phi[i]=1ll*i-1ll;
}
for(j=1;j<=tot;j++){
LL tmp=1ll*i*prime[j];
if(tmp>=N) break;
vis[tmp]=1;
if(i%prime[j]==0){
phi[tmp]=1ll*phi[i]*prime[j];
break;
}
else phi[tmp]=1ll*phi[i]*(prime[j]-1);
}
}
}
。。。。。。(还有很多筛子)
3、莫比乌斯反演的套路式

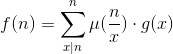

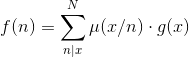
![f(x)=\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)==x]](http://img.e-com-net.com/image/info8/64d790b8b3a84fc8a72e125f913c1a2a.gif)

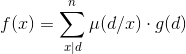
![g(x)=\sum_{x|d}^{n} \sum_{i=1}^{n} \sum_{j=1}^{m}[gcd(i,j)==d]](http://img.e-com-net.com/image/info8/57299f6145574de19c99fe9d4ebe2767.gif)
![g(x)=\sum_{i=1}^{n}\sum_{j=1}^{m}[x|gcd(i,j)]](http://img.e-com-net.com/image/info8/7f0f49571d9f4754a0778169279bc646.gif)