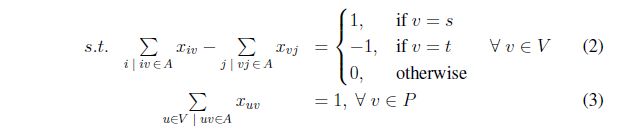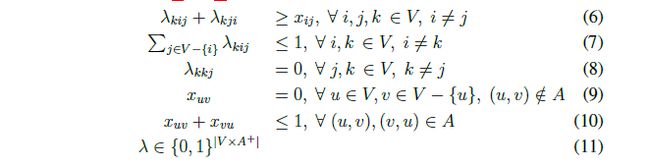MathProg语言简介(附带例子)
综述:我们在使用很多数学求解器时,会用到MathProg模型语言。MathProg语言能将一个纯数学语言描述的模型转化为求解器能读懂的格式。例如在使用线性规划求解器GLPK求解一个线性规划问题或者混合整数规划问题时,就需要用到MathProg语言。下面将以一个具体的例子深入浅出地讲解MathProg语言的使用规则。
一、数学模型:
二、写成MathProg格式
# 参数就是模型中的常量
param n,integer,>=0;
param s,integer,>=0;
param t,integer,>=0;
param c{(i, j) in A},integer,>=1,<=20;
#集合就是模型中下标的索引空间
set V := 0..n;
set P within V;
set Aplus := V cross V;
set Al := V cross Aplus;
set A within Aplus;
#变量就是模型中的变量
var x{(i, j) in Aplus}, binary;
var lamd{(k,i,j) in Al}, binary;
#目标函数
minimize obj : sum {(u,v) in A} c[u,v]*x[u,v];
#约束条件,必须给每个约束条件命名,名字后的花括号是约束条件中的索引空间,求和函数的索引范围放在sum后的花括号中。
s.t.
second1{v in V: v = s}: (sum{(i,v) in A} x[i,v]) - (sum{(v,j) in A} x[v,j]) = -1;
second2{v in V: v = t}: (sum{(i,v) in A} x[i,v]) - (sum{(v,j) in A} x[v,j]) = 1;
second3{v in V: v <> s and v <> t}: (sum{(i,v) in A} x[i,v]) - (sum{(v,j) in A} x[v,j]) = 0;
third{v in P}: sum{(u,v) in A} x[u,v]=1;
sixth{i in V,j in V,k in V: i <> j}: lamd[k,i,j]+lamd[k,j,i]>=x[i,j];
seventh{i in V,k in V: i <> k}: sum {j in V diff {i}} lamd[k,i,j]<=1;
eighth{j in V,k in V: k <> j}: lamd[k,k,j]=0;
ninth{u in V,v in V diff {u}: (u,v) not in A}: x[u,v]=0;
tenth{u in V,v in V: (u,v) in A and (v,u) in A}: x[u,v]+x[v,u]<=1;
#开始求解
solve;
#输出变量的值
display {(i,j) in A} x[i,j];
end;
推荐博文:
经典排序算法的C++实现