高等数学期末总复习DAY16.第一类曲线积分、第二类曲线积分、格林公式
DAY16.
人不能没有性情
文章目录
- DAY16.
- 第一类曲线积分
- 第二类曲线积分
- 格林公式
第一类曲线积分
对弧长的曲线积分
基本形式为: ∫ L f ( x , y ) d s \int_L f(x,y) d_s ∫Lf(x,y)ds
其中L为弧长、f(x,y)的点在弧长L上
又分为三种形式方程
- L : y = y ( x ) ; ⇒ ∫ a b f ( x , y ( x ) ) 1 + ( y x ′ ) 2 d x L : y = y(x) ; \Rightarrow \int_a^{b} f(x, y(x))\sqrt {1+(y'_x)^2}d_x L:y=y(x);⇒∫abf(x,y(x))1+(yx′)2dx
- L : x = x ( y ) ; ⇒ ∫ a b f ( x ( y ) , y ) 1 + ( x y ′ ) 2 d y L : x = x(y) ; \Rightarrow \int_a^{b} f(x(y), y)\sqrt {1+(x'_y)^2}d_y L:x=x(y);⇒∫abf(x(y),y)1+(xy′)2dy
- L : { x = x ( t ) y = y ( t ) ⇒ ∫ t 1 t 2 f ( x ( t ) , y ( t ) ) ( d x d t ) 2 + ( d y d t ) 2 d t L:\begin{cases} x = x(t) \\ y = y(t) \end{cases} \Rightarrow \int_{t_1}^{t_2} f(x(t),y(t)) \sqrt{(\frac{d_x}{d_t})^2+(\frac{d_y}{d_t})^2}d_t L:{x=x(t)y=y(t)⇒∫t1t2f(x(t),y(t))(dtdx)2+(dtdy)2dt
例题
求 ∫ L ( x 2 + y 2 ) n d s \int_L (x^2+y^2)^n d_s ∫L(x2+y2)nds其中L由圆周 x = a cos t , y = a sin t ( 0 ⩽ t ⩽ 2 π ) x = a \cos t ,y = a\sin t(0\leqslant t \leqslant 2 \pi) x=acost,y=asint(0⩽t⩽2π)围成
解:
依题意可知这是上面的第三种情况:
∫ L ( x 2 + y 2 ) n d s \int_L (x^2+y^2)^n d_s ∫L(x2+y2)nds
= ∫ 0 2 π ( a 2 cos 2 t + a 2 sin 2 t ) n ( − a sin t ) 2 + ( a cos t ) 2 d t =\int_0^{2 \pi}(a^2\cos^2 t+a^2\sin^2t)^n \sqrt{(-a\sin t)^2+(a\cos t)^2}d_t =∫02π(a2cos2t+a2sin2t)n(−asint)2+(acost)2dt
= ∫ 0 2 π a 2 n a d t =\int_0^{2 \pi} a^{2n} a d_t =∫02πa2nadt
= 2 π a 2 n + 1 =2\pi a^{2n+1} =2πa2n+1
第二类曲线积分
对坐标的曲线积分
∫ L P ( x , y ) d x + Q ( x , y ) d y \int_LP(x,y)d_x + Q(x,y)d_y ∫LP(x,y)dx+Q(x,y)dy
举一例:
L : y = y ( x ) ⇒ ∫ a b P ( x , y ( x ) ) d x + Q ( x , y ( x ) ) y ′ ( x ) d x L : y = y(x) \Rightarrow \int_a^b P(x,y(x))d_x+Q(x,y(x))y'(x)d_x L:y=y(x)⇒∫abP(x,y(x))dx+Q(x,y(x))y′(x)dx
例题
求 ∫ L ( x 2 − y 2 ) d x \int_L (x^2 - y^2) d_x ∫L(x2−y2)dx其中L是 y = x 2 y = x^2 y=x2从点(0,0)到(2,4)的一段弧
解:化为X形区域可得:
= ∫ 0 2 ( x 2 − ( x 2 ) 2 ) d x =\int_0^2 (x^2 - (x^2)^2) d_x =∫02(x2−(x2)2)dx
= − 56 15 = - \frac{56}{15} =−1556
格林公式
要使用格林公式要满足一下三点:
- 积分区域封闭
- 正向
- D内 φ Q φ x , φ P φ y \frac{\varphi Q}{\varphi x},\frac{\varphi P}{\varphi y} φxφQ,φyφP存在且连续
例题
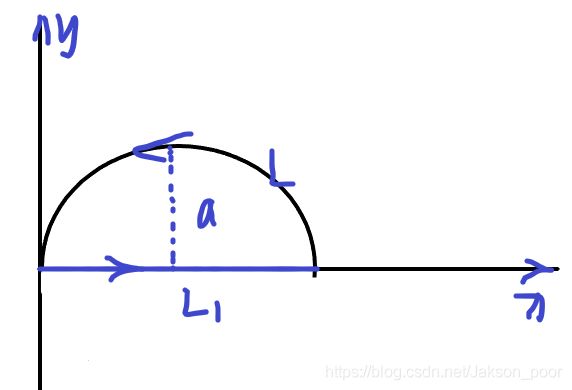
计算 ∫ L ( e x sin y − 2 y ) d x + ( e x cos y − 2 ) d y \int_L (e^x \sin y - 2y)d_x + (e^x \cos y - 2)d_y ∫L(exsiny−2y)dx+(excosy−2)dy其中L为:
其中L为原曲线,我们做一条辅助线L1 ,图中已标明方向
L = { y = 0 0 ⩽ x ⩽ 2 a L = \begin{cases} y = 0 \\ 0 \leqslant x \leqslant 2a \end{cases} L={y=00⩽x⩽2a
此时整个方程满足格林公式的要求
∫ L ( e x sin y − 2 y ) d x + ( e x cos y − 2 ) d y \int_L (e^x \sin y - 2y)d_x + (e^x \cos y - 2)d_y ∫L(exsiny−2y)dx+(excosy−2)dy
= ∬ D x o y ( e x cos y − ( e x cos y − 2 ) ) d x d y = \iint_{D_{xoy}} (e^{x}\cos y - (e^x \cos y -2))d_xd_y =∬Dxoy(excosy−(excosy−2))dxdy
= 2 ∬ D x o y d x d y =2 \iint_{D_{xoy}}d_xd_y =2∬Dxoydxdy
= 2 ∗ 1 2 π a 2 =2 * \frac{1}{2} \pi a^2 =2∗21πa2
= π a 2 = \pi a^2 =πa2