Verilog RTL 新手代码设计 （多路译码器、加法器、乘法器）

6.多路译码器

实现3－8译码器，使用case 语句实现，注意，一定要把case的情况写全，或者要加上default，代码如下：

// module top
module top(
  IN        ,   // input  
  OUT       );  // output 

input [2:0] IN;
output[7:0] OUT;

reg   [7:0] OUT;
// get the OUT
always @ (IN) begin
  case(IN)
    3'b000: OUT = 8'b0000_0001;
    3'b001: OUT = 8'b0000_0010;
    3'b010: OUT = 8'b0000_0100;
    3'b011: OUT = 8'b0000_1000;
    3'b100: OUT = 8'b0001_0000;
    3'b101: OUT = 8'b0010_0000;
    3'b110: OUT = 8'b0100_0000;
    3'b111: OUT = 8'b1000_0000;
    //  full case 不需要写default，否则一定要有default
  endcase
end
endmodule

RTL视图：

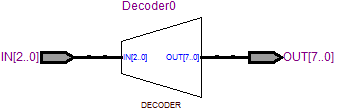
3－8译码器资源消耗：

接着实现4-16译码器，代码如下：

module top(
IN,
OUT);

input [3:0] IN;
output [15:0] OUT;

reg [15:0] OUT;
//get the OUT
always @(IN)
begin
  case(IN)
    4'b0000: OUT = 16'b0000_0000_0000_0001;
    4'b0001: OUT = 16'b0000_0000_0000_0010;
	4'b0010: OUT = 16'b0000_0000_0000_0100;
	4'b0011: OUT = 16'b0000_0000_0000_1000;
	4'b0100: OUT = 16'b0000_0000_0001_0000;
	4'b0101: OUT = 16'b0000_0000_0010_0000;
	4'b0110: OUT = 16'b0000_0000_0100_0000;
	4'b0111: OUT = 16'b0000_0000_1000_0000;
	4'b1000: OUT = 16'b0000_0001_0000_0000;
	4'b1001: OUT = 16'b0000_0010_0000_0000;
	4'b1010: OUT = 16'b0000_0100_0000_0000;
	4'b1011: OUT = 16'b0000_1000_0000_0000;
	4'b1100: OUT = 16'b0001_0000_0000_0000;
	4'b1101: OUT = 16'b0010_0000_0000_0000;
	4'b1110: OUT = 16'b0100_0000_0000_0000;
	4'b1111: OUT = 16'b1000_0000_0000_0000;
  endcase
end
endmodule

RTL View：

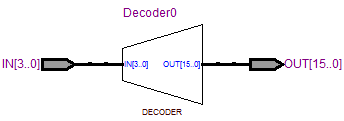
4－16译码器资源消耗：

通过对比发现，4－16译码器资源消耗约为3－8译码器资源消耗的2倍。

7.加法器

加法器是很常用的电路，主要常用的形式包括

• 无符号加法器，输入和输出数据都是无符号的整数，常用于计数器累加和计算地址序号
• 补码加法器，输入和输出数据都是2补码形式的有符号数，常用于数字信号处理电路

无符号加法器

输入和输出数据都是无符号的整数，常用于计数器累加和计算地址序号
verilog代码如下：

module top(
  IN1   ,
  IN2   ,
  OUT   );
input[3:0] IN1, IN2;
output[4:0] OUT;
reg[4:0] OUT;
always@(IN1 or IN2) begin // 生成组合逻辑的always 块
  OUT = IN1 + IN2;
end
endmodule 

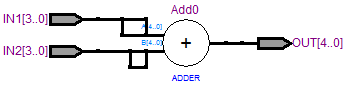
RTL View：

波形仿真：

可以发现加法器的输入数据和对应结果在时间上是有延迟的，这是组合逻辑门的延迟造成的，延迟长度大约在8ns到9ns左右。
当把加法器的输出信号改成4比特位宽时，我们会发现由于两个输入IN1和IN2最高为均为1时，会产生进位，从而发生错误。
波形仿真：

把加法器的输入信号改成8比特位宽式：
波形仿真：

从上图我们会发现8比特输入位宽和4比特输入位宽的情况对比，延迟时间并没有相差多少。

补码加法器

输入和输出数据都是2补码形式的有符号数，常用于数字信号处理电路
verilog代码如下：

module top(
  IN1   ,
  IN2   ,
  OUT   );
input signed [3:0] IN1, IN2;
output signed [4:0] OUT;
reg signed [4:0] OUT;
always@(IN1 or IN2) begin // 生成组合逻辑的always 块
  OUT = IN1 + IN2;
end
endmodule 

RTL View：

波形仿真：

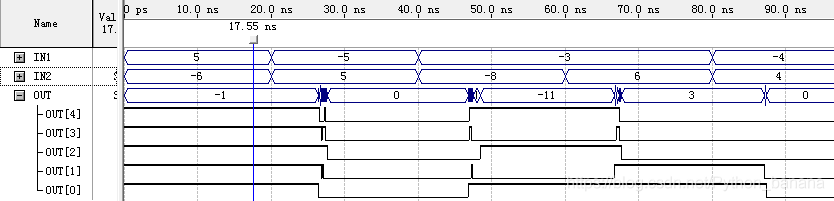
从图中，我们可以看出将补码取反加1后是正确的，验证了实验的正确。
下面对原实验参数进行改动进行观察：
当把加法器的输出信号改成4比特位宽时，波形仿真：

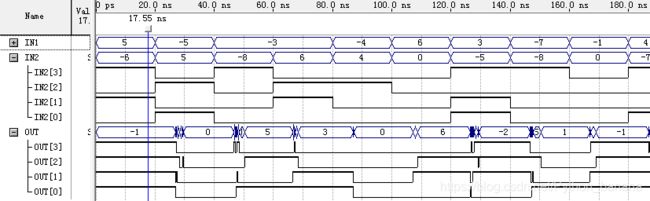
从图中可以发现当两个输入IN1和IN2的符号位均为1时，也就是都是负数时，因为有进位，所以会出错。

当把加法器的输入信号改成8比特位宽时，波形仿真：

通过和4比特输入位宽的情况对比观察加法器的输出延迟，我们发现延迟时间几乎一致。

带流水线的加法器

我们在无符号加法器中将输入和输出都添加了流水线D触发器，从来组成带流水线的加法器，verilog代码如下：

module top(
  IN1   ,
  IN2   ,
  CLK   ,
  OUT   );
input  [3:0] IN1, IN2;
input CLK;
output  [4:0] OUT;
reg [3:0] in1_d1R, in2_d1R;
reg  [4:0] adder_out, OUT;
always@(posedge CLK) begin // 生成D触发器的always块
  in1_d1R <= IN1;
  in2_d1R <= IN2;
  OUT     <= adder_out;
end
always@(in1_d1R or in2_d1R) begin // 生成组合逻辑的always 块
  adder_out = in1_d1R + in2_d1R;
end
endmodule 

RTL View：

波形仿真：

上图为带流水线的无符号加法器的仿真图，
下面为不带流水线的无符号加法器的仿真图：

通过上面两幅图片的对比发现：
输入信号为8比特位宽流水线无符号加法器信号输出延迟变长，同时有毛刺时间长度减小。

8.乘法器

先要强调的是，乘法器是一种奢侈品会消耗大量的组合电路逻辑资源，一定要慎重使用。

Verilog代码如下：

////////////////////  无符号的乘法器  /////////////////////////
module top(
  IN1   ,
  IN2   ,
  OUT   );
 input [3:0] IN1, IN2;
 output [7:0] OUT;
 reg [7:0] OUT;
always@(IN1 or IN2) begin // 生成组合逻辑的always 块
  OUT = IN1 * IN2;
end
endmodule 
////////////////////  有符号的2补码乘法器  /////////////////////////
module top(
  IN1   ,
  IN2   ,
  OUT   );
 input signed[3:0] IN1, IN2;
 output signed [7:0] OUT;
 reg signed[7:0] OUT;
 always@(IN1 or IN2) begin // 生成组合逻辑的always 块
  OUT = IN1 * IN2;
end
endmodule 

RTL View：

无符号乘法器波形仿真：

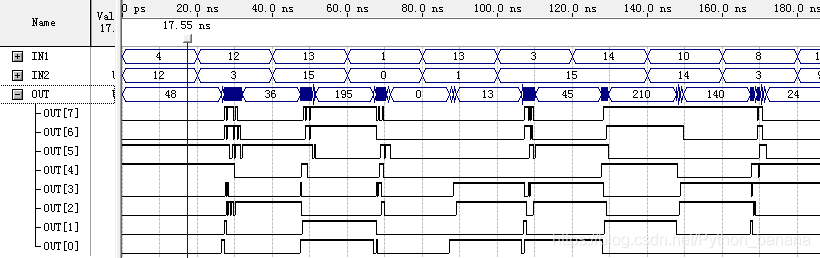
从上图我们可以看出，毛刺非常多。

有些FPGA芯片内部有固化的硬件乘法器，对于这样的芯片，代码中的乘号 * 会变成芯片中的乘法器。对于内部没有乘法器的FPGA芯片，代码中的乘号就会用逻辑单元拼接成加法器，再用加法器拼接成乘法器。

下面进行一些参数的改变：
当输入位宽为8比特时：

module top(
IN1,
IN2,
CLK,
OUT);
input [7:0] IN1,IN2;
input CLK;
output [15:0] OUT;
reg [7:0] in1_d1R,in2_d1R;
reg [15:0] multier_out,OUT;
always @(posedge CLK)
begin
  in1_d1R<=IN1;
  in2_d1R<=IN2;
  OUT    <=multier_out;
end
always @(in1_d1R or in2_d1R)
begin
  multier_out = in1_d1R * in2_d1R;
end
endmodule

波形仿真：

毛刺时间长度大约为14ns左右。

选一款没有硬件乘法器的FPGA芯片（例如Cyclone EP1C6）对比8比特的乘法器和加法器两者编译之后的资源开销(Logic Cell的数目）

Cyclone EP1C6的乘法器资源消耗：

Cyclone EP1C6的加法器资源消耗：

从上图的对比，我们可以发现，乘法器消耗的资源比加法器消耗的资源多很多。

下面设计带流水线的乘法器，其Verilog代码如下：

module top(
IN1,
IN2,
CLK,
OUT);
input [7:0] IN1,IN2;
input CLK;
output [15:0] OUT;
reg [7:0] in1_d1R,in2_d1R;
reg [15:0] multier_out,OUT;
always @(posedge CLK)
begin
  in1_d1R<=IN1;
  in2_d1R<=IN2;
  OUT    <=multier_out;
end
always @(in1_d1R or in2_d1R)
begin
  multier_out = in1_d1R * in2_d1R;
end
endmodule

带流水线乘法器波形仿真：

不带流水线乘法器波形仿真（上面已经有的）：

通过波形仿真对比，我们可以发现，带流水线的乘法器其毛刺明显减少。