LCT总结笔记
LCT的定义和性质
LCT在树链剖分的基础上,还可以滋磁动态连/删边等操作。
LCT维护的是splay组成的森林,有以下性质:
1.每个splay中序遍历得到的节点序列深度是递增的,序列深度之间两两相差1。
2.每个节点被包含且仅被包含于一个splay中。
3.若父亲和孩子在同一个splay中,则它们连的是实边,反之是虚边。
性质1推论:原树中一个节点向孩子最多只能连一条实边。
证明:原树中,一个节点的两个孩子不可能在同一棵splay中,否则会无法使节点序列深度单调递增。也就是说,原树中每个节点最多只能向孩子连一条实边,向其他孩子连的都是虚边。
性质3推论:若两个节点在同一个splay中,则它们之间有一条实边路径相连。
证明:显然。
在LCT中,无法从虚边的父亲访问孩子,只能从虚边的孩子访问父亲。也就是说,虚边是“认父不认子”的。
access操作
access操作:打通某个节点到根节点的实链,即把这个节点到根节点的路径上的边都改为实边,然后把连了两条实边的节点的另一条实边改为虚边。
嫖来YangZhe论文里的图:以下面这棵树为例。假设原树中一开始实边、虚边这样区分:

假设现在想access(N),即把N到A的实链路径打通。
首先需要让N所在splay中深度最浅的节点打通它与父亲的实边。也就是说,需要让L与I变成实边。
L与I变成实边后,I原来连的实边就要变成虚边,否则一个节点就会向孩子连两条实边,这是不符合性质1推论的。原树变成这样(注意节点K,I,L附近边的变化):

这样的操作成功地让L和I的实边打通了!同理,我们继续让H和I之间连实边。为了让H满足只向孩子连一条实边的性质,要让H本来连向孩子J的实边变成虚边。
接着,同理把A和C的实边打通,把A和B的实边变成虚边,就打通了从N到A的路径。
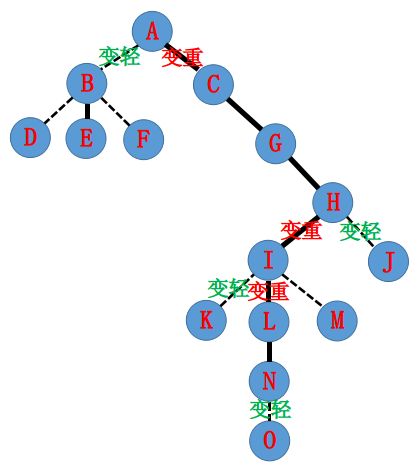
(图中让N与O之间变成轻边只是为了让程序易于实现,接下来会说实现方式)
现在总结打通路径的过程:
对于每个节点,想要打通它与根节点之间的路径,需要让它到根节点路径上原来是虚边的边变成实边(废话)。然后让连了两条实边的节点的另一条实边变成虚边。
因此,每次找到当前splay中深度最浅的节点,此时它与父亲的边一定是虚边。否则它与父亲在同一棵splay中,这样它就不是splay中深度最浅的节点,矛盾。
把它与父亲之间的边改为实边。因为它的深度肯定比父亲的深度大,所以直接把父亲节点的右孩子设为它就好了(这样也顺便把父亲原来连向孩子的实边断掉了)。
代码可以表示成这样:
void access(int x) {
for(int y=0;x;y=x,x=w[x].fa) { //y表示下面的splay的深度最浅的节点。x表示y的父亲,x与y连的是虚边。
splay(x);
w[x].ch[1]=y;
pushup(x); //维护x的信息
}
}
发现这样access后,access的节点原来连向孩子的实边变成了虚边。于是它变成了它所在splay中深度最大的节点。
makeroot操作
makeroot是“将原树的根设置为某个节点”的操作。makeroot会使要设为根的节点变为深度最小的节点,而单纯的access会让这个节点变为它所在splay中深度最大的节点。
考虑把 x x x设为根会对它的splay产生什么影响。LCT的性质1指出:每个splay中序遍历得到的节点序列深度是递增的,序列深度之间两两相差1。所以access(x)后 x x x所在splay中序遍历的深度应为 1 , 2 , . . . , d e p t h ( x ) 1,2,...,depth(x) 1,2,...,depth(x)。
把 x x x换为根后,yy一下可以发现中序遍历的深度将会变为 d e p t h ( x ) , d e p t h ( x ) − 1 , . . . , 1 depth(x),depth(x)-1,...,1 depth(x),depth(x)−1,...,1。然后可以通过互换所有节点左右孩子来维护splay性质,通过lazytag实现。
inline void pushrev(int x) {
swap(lc(x),rc(x));
w[x].tag^=1;
}
void makeroot(int x) {
access(x);
splay(x);
pushrev(x);
}
findroot操作
findroot是找到 x x x所在的原树中的根,也就是找到深度最浅的节点。
可以通过打通 x x x到根路径,把 x x x旋转到根,然后不断地找左孩子实现。
当然,不断找左孩子的时候要注意pushdown。
int findroot(R x){
access(x); splay(x);
while(lc(x)) {
pushdown(x);
x=lc(x);
}
splay(x);
return x;
}
link操作
link操作是在 x , y x,y x,y之间连一条轻边。如果 x , y x,y x,y已经在同一个联通块中则不用连边。判断 x , y x,y x,y在同一个联通块中的方式是先makeroot(x),然后findroot(y)==x说明在同一个联通块中。
inline void link(int x,int y) {
makeroot(x);
if(findroot(y)!=x) {
w[x].fa=y;
}
}
cut操作
cut操作是删除 x , y x,y x,y之间的边(无论虚实)。如果保证 x , y x,y x,y在同一个联通块中 x , y x,y x,y之间有一条边相连,那么makeroot(x),access(y)后把 x x x和 y y y之间的边断去即可。
判断 x , y x,y x,y在同一个联通块中的方法是makeroot(x)然后判断findroot(y)==x。而现在仍需判断 x , y x,y x,y之间是否有一条边。
注意到一通makeroot和findroot使我们把 x x x旋转到了它所在splay的根,且 x x x是splay中深度最小的节点。如果 x , y x,y x,y之间有一条边,那么 y y y深度一定比 x x x大1。
因此只需要判断 y y y父亲为 x x x且 y y y左孩子为空即可。(或者可以判断 x x x右孩子为 y y y且 y y y左孩子为空)
void cut(int x,int y) {
makeroot(x);
if(findroot(y)==x && w[y].father==x && !w[y].ch[0]) {
w[y].father=w[x].ch[1]=0;
pushup(x);
}
}
split操作
split操作是拉出一条 x x x到 y y y的splay。这个操作就比较显然了。
void split(int x,int y) {
makeroot(x);
access(y);
splay(y);
}