解读：一种来自Facebook团队的大规模时间序列预测算法（附github链接）

写在前面

下面这篇文章的内容主要是来自Facebook团队的论文《Forecast at Scale》，这篇论文介绍了一种时间序列预测算法Prophet，该算法结合了时间序列分解以及机器学习算法，并且可以对存在缺失值和异常值的时间序列进行预测。除此之外，该算法也被Facebook用于各项业务场景中。原论文和github链接在文末进行获取。

1

摘要

时间序列预测是一项常见的数据科学任务，它可以协助我们进行容量规划、目标设置和异常检测等。尽管通过时间序列进行预测很重要，但研制具有生产可靠和高质量的预测模型仍然存在着严重的挑战——特别是对于一些多变的时间序列，并对于其先验知识相对较少时。为了解决这些挑战，这篇论文描述了一种“大规模”预测的实用方法，该方法将可配置模型与在循环中分析的性能分析相结合，并针对于此提出了一个高解释性的多模块回归模型。

2

模型构建

由于现实中，时间序列常常是由趋势项，季节项，节假日效应和突发事件以及残差项组成，所以Prophet算法采用了时间序列分解的方法，它把时间序列分为了这几个部分：

   

其中的   表示趋势项，它体现了时间序列的非周期变化趋势；   表示季节项，它体现了时间序列的周期性变化，如每周，每年的这种季节性变化；   表示节假日项，它体现了节假日等持续一天到几天的无规律变化；最后的   表示残差项，通常是正态分布的。然后各项分别被拟合，最后的累加结果即是Prophet算法的预测结果。

其中，Facebook对于Prophet算法的这种设定是一种 generalized additive model (GAM)，其中GAM的形式具有很多优点，包括它容易被分解以及适应新的成分，并且与ARIMA模型不同的是，测量数据还不需要有规律的间隔，我们也不需要插入缺失的值或者删除离群值。并且，预测模型有很容易解释的参数，可以由分析人员更改这些参数以对预测进行假设，这样尤其是对于一些要求高可解释性的场景，如金融衍生品价格的预测，可以更好地提供一个可解释性的角度。

下面对每一项的拟合进行分别的介绍：

1、趋势项模型

其中趋势项模型根据应用背景不同，引入了两种不同的函数，一是逻辑回归函数（logistic function），另一个是基于分段线性函数（piecewise linear function。

当问题背景是增长型预测时，如预测人口的增长模式，或者是一个地区Facebook用户的增长。它会根据环境或者地区的承载力达到一定的饱和程度，所以这种情况下趋势项是以逻辑回归函数进行拟合的，即： 

其中，C表示承载容量，k表示增长率，m表示一个偏置参数。然而在现实情况下，承载容量和增长率不会一直保持不变，也即都不可能是常数。其中承载容量表示为C(t)，即是一个时变的形式。而实际情况下，如Facebook的一些变革或者新产品的推出，可能会导致增长率的阶段性变化，所以增长率的设置上加入了变点的考虑，即不同时段的增长率会发生变化。其最终形式表示如下，即是一个分段的逻辑回归函数模型：

用于预测不出现饱和增长的问题时，分段线性函数就作为其趋势项的模型了。其表现形式为：

2、季节项模型

商业时间序列由于会代表的人类行为，往往具有多期的季节性。例如，一周工作5天会对每周重复的时间序列产生影响，而假期计划和学校假期则会对每年重复的时间序列产生影响。所以时间序列出现的周期性变化也必须被考虑进去。而数学中描述周期性的函数通常会使人想到正弦和余弦函数。所以原文中采用了傅里叶级数来估计季节项，即如下所示：

其中上式中P=365.25表示是年为周期的数据，P=7则表示以周为周期的数据。其中，关于参数N的选择，作者根据先验知识得到对于年为周期的数据N=10比较合适，对于周为周期的数据N=3比较合适。另外，关于模型参数的选择也可以通过AIC、BIC等准则进行选取。

3、节假日效应

节假日等事件对许多业务时间序列会造成某种程度上的冲击，并且它们通常不遵循周期性模式，因此节假日等事件的影响不能很好地用一个平稳的周期来建模。所以在Prophet中，作者提出了通过收集了各个国家的节假日信息，将加入到了模型中，如下图表示了一个假期列表的例子。

为了描述某个节假日的影响大小和跨度范围，文中通过一个累加的正态分布的形式来表示这个影响：

其中，Z(t)表示每个假期所有假期的集合，K表示每个假期对应的影响范围，它服从于正态分布：

其中，这个正态分布的方差表示影响程度的大小，值越大表示影响越大，值越小表示影响越小。除此之外，用户也可以加入自己自定义的一些节假日，如双十一等。

至此，文章提出的模型架构的每个模块就已经介绍完成了，下面就是如何对这个模型通过数据进行拟合了。文中是通过 L-BFGS算法来进行最大后验估计以获取最优参数，其中，L-BFGS是一种求解无约束非线性规划问题最常用的方法，它具有收敛速度快、内存开销少等优点。

3

实验验证

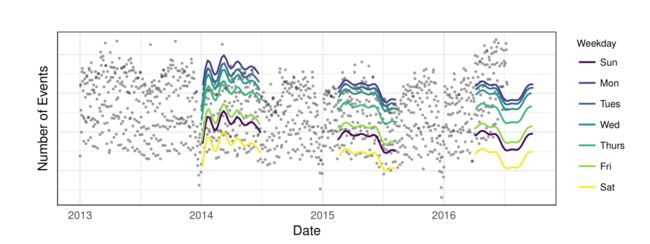
下面是Prophet模型用于Facebook事件数量的预测：

下图表示的是Prophet模型对所有数据的预测效果，其中实线表示的样本内预测，虚线表示的样本外的预测。

4

结论

从前面的分析可以看出，对于具有时间周期性和趋势性的一些领域的时间序列来说，通过Prophet进行拟合可以获得不错的预测效果。除此之外，Facebook将这种方法进行了开源，对于一些不明白其算法原理的人来说也可以直接通过它进行调用以解决一系列问题，同时它具有较高的可解释性，所以可以充分利用先验知识。虽然这个算法对于一些周期强的数据预测可获取不错效果，但是如果我们处理的时间序列不具有周期性而是一种多变的序列，则它可能就会失效了，所以还需要根据实际问题背景来进行选择。

后面我们也将介绍如何使用Prophet算法，并将其应用于金融衍生品序列的预测之中。

该算法的github链接是：https://github.com/facebook/prophet

论文链接：https://peerj.com/preprints/3190.pdf

往期精彩回顾



适合初学者入门人工智能的路线及资料下载机器学习在线手册深度学习在线手册AI基础下载（pdf更新到25集）本站qq群1003271085，加入微信群请回复“加群”获取一折本站知识星球优惠券，复制链接直接打开：https://t.zsxq.com/yFQV7am喜欢文章，点个在看