MATLAB 使用CNN拟合回归模型预测手写数字的旋转角度（卷积神经网络）

学习来源自mathworks的官方范例，个人学习使用，在个人项目上可以按照需求变化数据集来实现CNN回归计算

数据集生成方法可以参考：https://blog.csdn.net/qingfengxd1/article/details/105931988

%% 加载数据
%% 数据集包含手写数字的合成图像，以及每幅图像旋转的对应角度(以角度为单位)。
%% 使用digitTrain4DArrayData和digitTest4DArrayData将训练和验证图像加载为4D数组。
%% 输出YTrain和YValidation是以角度为单位的旋转角度。每个训练和验证数据集包含5000张图像。
[XTrain, ~, Ytrain] = digitTrain4DArrayData;
[XValidation, ~, YValidation] = digitTest4DArrayData;
%% 随机显示20张训练图像
numTrainImages = numel(YTrrain);
figure;
idx = randperm(numTrainImages, 20);
for i = 1 : numel(idx)
    subplot(4, 5, i);
    imshow(XTrain(:, :, :, idx(i)))
    drawnow
end

%% 数据归一化处理
%% 当训练神经网络时，确保你的数据在网络的所有阶段都是标准化的通常是有帮助的。
%% 归一化有助于使用梯度下降来稳定和加速网络训练。
%% 如果您的数据规模太小，那么损失可能会变成NaN，并且在培训期间网络参数可能会出现分歧。
%% 标准化数据的常用方法包括重新标定数据，使其范围变为[0,1]或使其均值为0，标准差为1。
%{
你可以标准化以下数据:
1、输入数据。在将预测器输入到网络之前对它们进行规范化。在本例中，输入图像已经标准化为[0,1]范围。
2、层输出。您可以使用批处理规范化层对每个卷积和完全连接层的输出进行规范化。
3、响应。如果使用批处理规范化层对网络末端的层输出进行规范化，则在开始训练时对网络的预测进行规范化。
        如果响应的规模与这些预测非常不同，那么网络训练可能无法收敛。
        如果你的回答没有得到很好的扩展，那么试着将其标准化，看看网络培训是否有所改善。
        如果在训练前对响应进行规范化，则必须转换训练网络的预测，以获得原始响应的预测。
%}

%% 一般来说，数据不必完全标准化。
%% 但是，如果在本例中训练网络来预测100*YTrain或YTrain+500而不是YTrain，那么损失就变成NaN，
%% 当训练开始时，网络参数就会出现分歧。
%% 即使网络预测aY + b和网络预测Y之间的唯一区别是重新调整最终完全连接层的权重和偏差，这些结果仍然会出现。
%% 如果输入或响应的分布非常不均匀或倾斜，还可以执行非线性转换(例如，取对数)

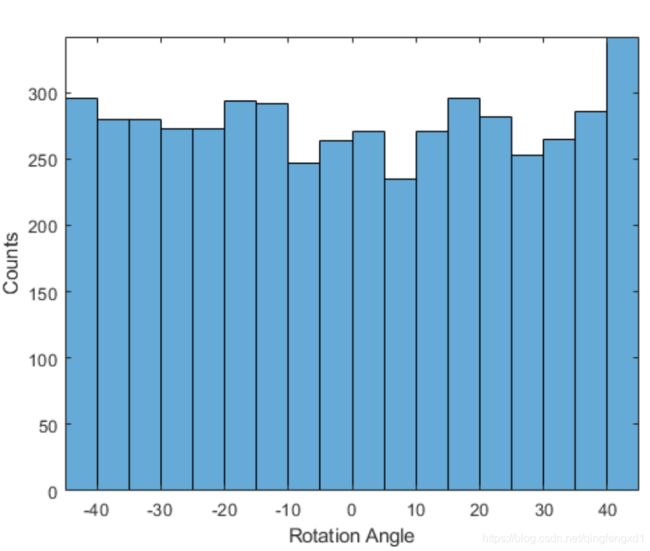
%% 绘制响应分布：在分类问题中，输出是类概率，类概率总是归一化的。
figure;
histogram(YTrain)
axis tight
ylabel('Counts')
xlabel('Rotation Angle')

通常，数据不必完全归一化。但是，如果在此示例中训练网络来预测 100*YTrain 或 YTrain+500 而不是 YTrain，则损失将变为 NaN，并且网络参数在训练开始时会发生偏离。即使预测 aY + b 的网络与预测 Y 的网络之间的唯一差异是对最终全连接层的权重和偏置的简单重新缩放，也会出现这些结果。

如果输入或响应的分布非常不均匀或偏斜，您还可以在训练网络之前对数据执行非线性变换（例如，取其对数）。

%% 创建网络层
%% 第一层定义输入数据的大小和类型。输入的图像大小为28×28×1。创建与训练图像大小相同的图像输入层。
%% 网络的中间层定义了网络的核心架构，大部分计算和学习都在这个架构中进行。
%% 最后一层定义输出数据的大小和类型。对于回归问题，全连接层必须先于网络末端的回归层。
layers = [
    imageInputLayer([28 28 1])
    batchNormalizationLayer
    reluLayer
   
    averagePooling2dLayer(2, 'Stride', 2)
   
    convolution2dLayer(3, 16, 'Padding', 'same')
    batchNormalizationLayer
    reluLayer
   
    averagePooling2dLayer(2, 'Stride', 2)
   
    convolution2dLayer(3, 32, 'Padding', 'same')
    batchNormalizationLayer
    reluLayer
   
    concolution2dLayer(3, 32, 'Padding', 'same')
    batchNormalizationLayer
    reluLayer
   
    dropoutLayer(0.2)
    fullyConnectedLayer(1)
    regressionLayer];
%% 训练网络——Options
%% Train for 30 epochs 学习率0.001 在20个epoch后降低学习率。
%% 通过指定验证数据和验证频率，监控培训过程中的网络准确性。
%% 根据训练数据对网络进行训练，并在训练过程中定期对验证数据进行精度计算。
%% 验证数据不用于更新网络权重。打开训练进度图，并关闭命令窗口输出。
miniBatchSize = 128;
validationFrequency = floor(numel(YTrain) / miniBatchSize);
options = trainingOptions('sgdm', ...
    'MiniBatchSize', miniBatchSize, ...
    'MaxEpochs', 30, ...
    'InitialLearnRate', 1e-3, ...
    'LearnRateSchedule', 'piecewise', ...
    'LearnRateDropFactor', 0.1, ...
    'LearnRateDropPeriod', 20, ...
    'Shuffle', 'every-epoch', ...
    'ValidationData', {XValidation, YValidation}, ...
    'ValidationFrequency', validationFrequency, ...
    'Plots', 'training-progress', ...
    'Verbose', false);
net = trainNetwork(XTrain, YTrain, layer, options)

使用 trainNetwork 创建网络。如果存在兼容的 GPU，此命令会使用 GPU。否则，trainNetwork 将使用 CPU。在 GPU 上进行训练需要具有 3.0 或更高计算能力的支持 CUDA® 的 NVIDIA® GPU。

检查 net 的 Layers 属性中包含的网络架构的详细信息。

net.Layers

基于验证数据评估准确度来测试网络性能。使用 predict 预测验证图像的旋转角度。

YPredicted = predict(net,XValidation);

评估性能

通过计算以下值来评估模型性能：

1. 在可接受误差界限内的预测值的百分比

2. 预测旋转角度和实际旋转角度的均方根误差 (RMSE)

计算预测旋转角度和实际旋转角度之间的预测误差。

predictionError = YValidation - YPredicted;

计算在实际角度的可接受误差界限内的预测值的数量。将阈值设置为 10 度。计算此阈值范围内的预测值的百分比。

thr = 10;
numCorrect = sum(abs(predictionError) < thr);
numValidationImages = numel(YValidation);

accuracy = numCorrect/numValidationImages

使用均方根误差 (RMSE) 来衡量预测旋转角度和实际旋转角度之间的差异。

squares = predictionError.^2;
rmse = sqrt(mean(squares))

显示每个数字类的残差箱线图

boxplot 函数需要一个矩阵，其中各个列对应于各个数字类的残差。

验证数据按数字类 0-9 对图像进行分组，每组包含 500 个样本。使用 reshape 按数字类对残差进行分组。

residualMatrix = reshape(predictionError,500,10);

residualMatrix 的每列对应于每个数字的残差。使用 boxplot (Statistics and Machine Learning Toolbox) 为每个数字创建残差箱线图。

figure
boxplot(residualMatrix,...
    'Labels',{'0','1','2','3','4','5','6','7','8','9'})
xlabel('Digit Class')
ylabel('Degrees Error')
title('Residuals')

准确度最高的数字类具有接近于零的均值和很小的方差。

您可以使用 Image Processing Toolbox 中的函数来摆正数字并将它们显示在一起。使用 imrotate (Image Processing Toolbox) 根据预测的旋转角度旋转 49 个样本数字。

idx = randperm(numValidationImages,49);
for i = 1:numel(idx)
    image = XValidation(:,:,:,idx(i));
    predictedAngle = YPredicted(idx(i));  
    imagesRotated(:,:,:,i) = imrotate(image,predictedAngle,'bicubic','crop');
end

显示原始数字以及校正旋转后的数字。您可以使用 montage (Image Processing Toolbox) 将数字显示在同一个图像上。

figure
subplot(1,2,1)
montage(XValidation(:,:,:,idx))
title('Original')

subplot(1,2,2)
montage(imagesRotated)
title('Corrected')