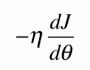机器学习之梯度下降法(Gradient Descent)
1.梯度下降法
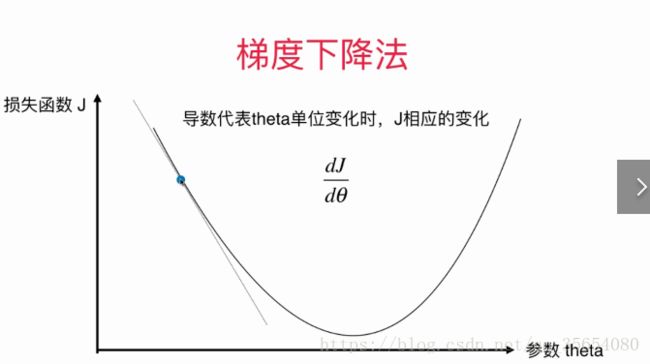
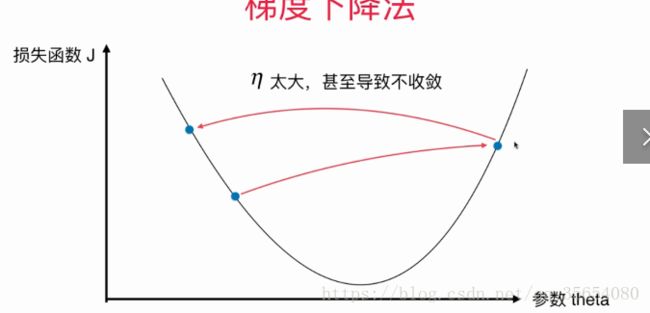
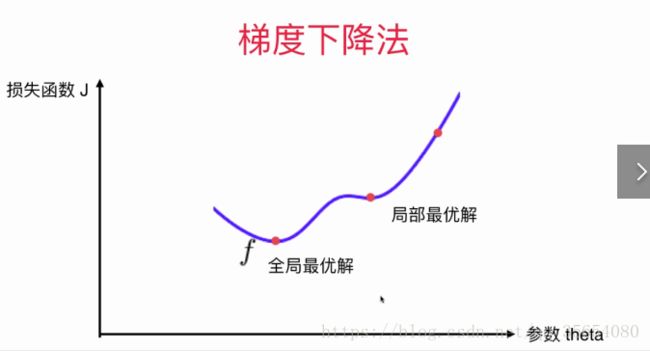
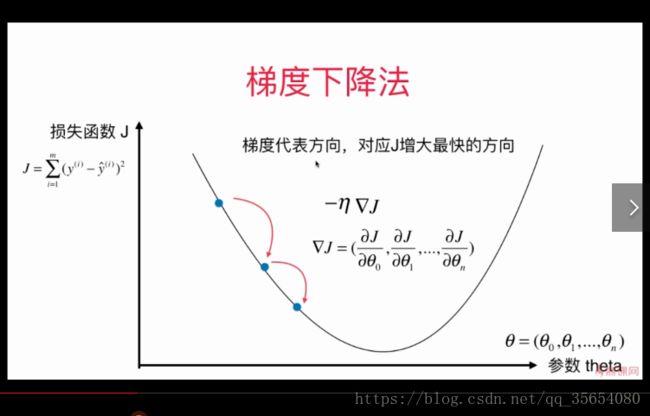
首先梯度下降法不是一个机器学习算法,而是一种基于搜索的最优化方法。它的作用是最小化一个损失函数。梯度上升法则是最大化一个效用函数。
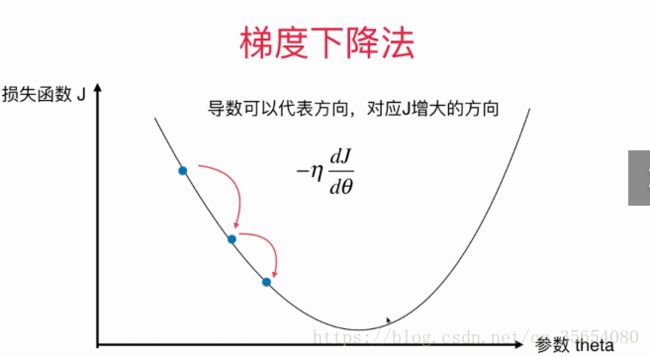
导数可以代表J 增大的方向,如上图一点导数为负值,说明J增大的方向是沿着X轴负方向。
模拟梯度下降法:
"""模拟梯度下降法"""
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)
plot_y = (plot_x - 2.5) ** 2 - 1
plt.plot(plot_x, plot_y)
plt.show()
def dJ(theta):
"""计算导数值"""
return 2 * (theta - 2.5)
def J(theta):
"""计算损失函数的值"""
return (theta - 2.5) ** 2 - 1
theta = 0.0
theta_history = [theta]
def gradient_descent(initial_theta,eta,epsilon=1e-8):
"""模拟梯度下降法"""
theta=initial_theta
theta_history.append(initial_theta)
while True:
gradient = dJ(theta)
last_theat = theta
theta = theta - eta * gradient
theta_history.append(theta)
if abs(J(theta)-J(last_theat)) < epsilon:
break
def plot_theta_history():
plt.plot(plot_x,J(plot_x))
plt.plot(np.array(theta_history),J(np.array(theta_history)),color='r')
plt.show()
eta = 0.8
theta_history=[]
gradient_descent(0.,eta)
plot_theta_history()
使用梯度下降训练:
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
def J(theta, X_b, y):
"""求损失函数"""
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
"""求梯度"""
# res = np.empty(len(theta))
# res[0] = np.sum(X_b.dot(theta) - y)
# for i in range(1, len(theta)):
# res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
# return res * 2 / len(X_b)
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
"""在线性回归模型中使用梯度下降法"""
import numpy as np
import matplotlib.pyplot as plt
from LinearRegression import LinearRegression
np.random.seed(666)
x=2*np.random.random(size=100)
y=x*3.+4.+np.random.normal(size=100)
X=x.reshape(-1,1)
plt.scatter(x,y)
plt.show()
lin_reg=LinearRegression()
lin_reg.fit_gd(X,y)
print(lin_reg.intercept_)
print(lin_reg.coef_)
"""使用梯度下降法前进行数据归一化"""
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from LinearRegression import LinearRegression
from model_selection import train_test_split
boston=datasets.load_boston()
X=boston.data
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
x_train,x_test,y_train,y_test=train_test_split(X,y,seed=666)
lin_reg=LinearRegression()
lin_reg.fit_normal(x_train,y_train)
print(lin_reg.score(x_test,y_test))
standardScaler=StandardScaler()
standardScaler.fit(x_train)
x_train_standard=standardScaler.transform(x_train)
x_test_standard=standardScaler.transform(x_test)
lin_reg2=LinearRegression()
lin_reg2.fit_gd(x_train_standard,y_train)
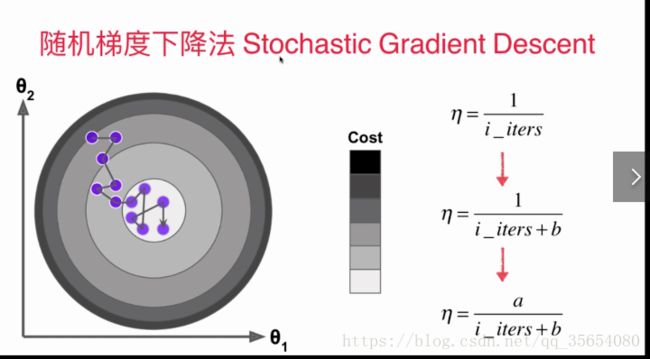
print(lin_reg2.score(x_test_standard,y_test))随机梯度下降法:
自己的随机梯度下降法
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert n_iters >= 1
def dJ_sgd(theta, X_b_i, y_i):
"""使用随机下降梯度法返回第i个样本的梯度"""
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters, t0=5, t1=50):
"""使用随机梯度下降法寻找theta"""
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b)
for cur_iter in range(n_iters):
indexes = np.random.permutation(m)"获取索引值"
X_b_new = X_b[indexes]
y_new = y[indexes]
for i in range(m):
gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
theta = theta - learning_rate(cur_iter * m + i) * gradient
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self分别使用自己的算法和sklearn中的随机梯度下降法:
"""使用自己的随机梯度下降法(数据是虚假的)"""
import numpy as np
import matplotlib.pyplot as plt
from LinearRegression import LinearRegression
m=10000
x=np.random.normal(size=m)
X=x.reshape(-1,1)
y=4.*x+3.+np.random.normal(0,3,size=m)
lin_reg=LinearRegression()
lin_reg.fit_sgd(X,y,n_iters=2)
print(lin_reg.coef_)
print(lin_reg.intercept_)
"""使用真实的数据,利用随机梯度下降法"""
from sklearn import datasets
from model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from LinearRegression import LinearRegression
boston=datasets.load_boston()
X=boston.data
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
x_train,x_test,y_train,y_test=train_test_split(X,y,seed=666)
standard=StandardScaler()
standard.fit(x_train)
x_train_standard=standard.transform(x_train)
x_test_standard=standard.transform(x_test)
lin_reg=LinearRegression()
lin_reg.fit_sgd(x_train_standard,y_train,n_iters=100)
print(lin_reg.score(x_test_standard,y_test))
"""scikit-learn中的SGD随机梯度下降法"""
from sklearn.linear_model import SGDRegressor
from sklearn import datasets
from model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
boston=datasets.load_boston()
X=boston.data
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
x_train,x_test,y_train,y_test=train_test_split(X,y,seed=666)
standard=StandardScaler()
standard.fit(x_train)
x_train_standard=standard.transform(x_train)
x_test_standard=standard.transform(x_test)
sgd_reg=SGDRegressor(n_iter=100)
sgd_reg.fit(x_train_standard,y_train)
print(sgd_reg.score(x_test_standard,y_test))