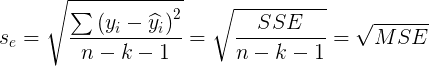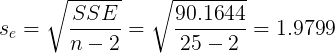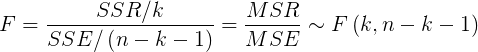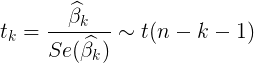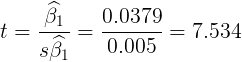回归分析-常用统计量含义解析
线性回归模型预测好坏,评判标准主要观察回归直线与各观测点的接近程度(即直线的拟合优度)。但是如何量化它们之间的接近程度呢?可使用以下常用统计量进行衡量。各统计量分解如下:
- SST总平方和

- SSR回归平方和

- SSE残差平方和

回归平方和是回归值与均值的离差平方和,可以看做由于自变量![]() 的变化引起的
的变化引起的![]() 的变化(即
的变化(即![]() 受
受![]() 的影响);
的影响);
残差平方和(或称误差平方和)是真实值与回归值的离差平方和,它是除了![]() 对
对![]() 的线性影响之外的其他因素引起的
的线性影响之外的其他因素引起的![]() 的变化部分,是不能由回归直线来解释的
的变化部分,是不能由回归直线来解释的![]() 的变差部分(即
的变差部分(即![]() 受其他因素的影响,如
受其他因素的影响,如![]() 对
对![]() 的非线性影响、测量误差等)。残差平方和描述了真实值与预测值之间的差异程度。
的非线性影响、测量误差等)。残差平方和描述了真实值与预测值之间的差异程度。
三个平方和的关系为:
总平方和(SST)= 回归平方和(SSR)+ 残差平方和(SSE)
- 判定系数
判定系数![]() 是对估计的回归方程拟合优度的度量。(即测度了回归直线对观测数据的拟合程度)
是对估计的回归方程拟合优度的度量。(即测度了回归直线对观测数据的拟合程度)
- 若所有观测点都落在回归直线上,残差平方和SSE=0,则
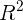 =1,拟合是完全的;
=1,拟合是完全的; - 如果
 的变化与
的变化与 无关,
无关, 完全无助于解释
完全无助于解释 的变差,
的变差,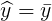 ,则
,则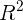 =0;
=0; 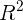 的取值范围是[0, 1];
的取值范围是[0, 1];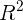 越接近1,表明回归平方和占总平方和的比例越大,回归直线与各观测点越接近,用
越接近1,表明回归平方和占总平方和的比例越大,回归直线与各观测点越接近,用 的变化来解释
的变化来解释 值变差的部分就越多,回归直线的拟合程度就越好;反之,
值变差的部分就越多,回归直线的拟合程度就越好;反之,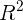 越接近0,回归直线的拟合程度就越差。
越接近0,回归直线的拟合程度就越差。
例子解释其含义:
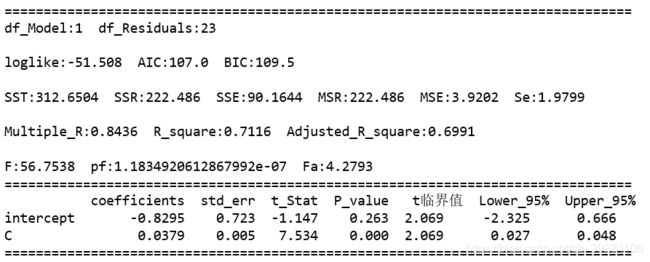
下图为不良贷款Y对贷款余额X构建的一元线性回归模型的回归分析结果,数据源可查看https://blog.csdn.net/qq_39284106/article/details/104156844
Q:计算不良贷款![]() 对贷款余额
对贷款余额![]() 回归的判定系数,并解释其意义?
回归的判定系数,并解释其意义?
A2:判定系数的实际意义是:在不良贷款取值的变差中,有71.16%可以由不良贷款与贷款余额之间的线性关系来解释,或者说,在不良贷款取值的变动中,有71.16%是由贷款余额所决定的。不良贷款取值的差异有2/3以上是由贷款余额决定的,可见二者之间有较强的线性关系。
调整的判定系数是用样本量![]() 和自变量的个数
和自变量的个数![]() 去调整
去调整![]() 的,其实际意义是在用样本量和模型中自变量个数进行调整后,能被因变量和自变量的一元或是多元回归方程所解释的比例为
的,其实际意义是在用样本量和模型中自变量个数进行调整后,能被因变量和自变量的一元或是多元回归方程所解释的比例为![]() 。
。
有了判定系数,为什么还需要调整的判定系数呢?
:是因为自变量个数的增加将影响到因变量的变差中被估计的回归方程所解释的比例。当增加自变量时,会使预测误差变得较小,从而减少残差平方和SSE。由于回归平方和 SSR=SST - SSE,当SSE变小时,SSR就会变大,从而使![]() 变大。如果模型中增加一个自变量,即使这个自变量在统计上并不显著,
变大。如果模型中增加一个自变量,即使这个自变量在统计上并不显著,![]() 也会变大。因此避免增加自变量而高估
也会变大。因此避免增加自变量而高估![]() ,需要同时考虑样本量和模型中自变量的个数的影响,这就使得
,需要同时考虑样本量和模型中自变量的个数的影响,这就使得![]() 的值永远小于
的值永远小于![]() ,而且
,而且![]() 的值不会由于模型中的自变量个数增加而越来越接近1。因此在多元回归分析中,通常用调整的判定系数。
的值不会由于模型中的自变量个数增加而越来越接近1。因此在多元回归分析中,通常用调整的判定系数。
Q:计算不良贷款![]() 对贷款余额
对贷款余额![]() 回归的调整的判定系数,并解释其意义?
回归的调整的判定系数,并解释其意义?
A2:它表示:在用样本量和模型中自变量个数进行调整后,在不良贷款取值的变差中,能被不良贷款和贷款余额的回归方程所解释的比例为69.91%。
- 复相关系数Multiple_R
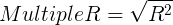
复相关系数度量了因变量同![]() 个自变量的相关程度。
个自变量的相关程度。
估计标准误差就是度量各个实际观测点在直线周围的散布状况的一个统计量。
估计标准误差是对误差项![]() 的标准差
的标准差![]() 的估计,它可以看做在排除了
的估计,它可以看做在排除了![]() 对
对![]() 的线性影响后,
的线性影响后,![]() 随机波动大小的一个估计量。
随机波动大小的一个估计量。
- 从估计标准误差的实际意义看,它反映了用估计的回归方程预测因变量
 时预测误差的大小。
时预测误差的大小。 - 各观测点越靠近直线,
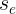 越小,回归直线对各观测点的代表性就越好,根据估计的回归方程进行预测也就越准确。
越小,回归直线对各观测点的代表性就越好,根据估计的回归方程进行预测也就越准确。 - 若各观测点全部落在直线上,则
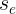 =0,此时用自变量来预测因变量是没有误差的。
=0,此时用自变量来预测因变量是没有误差的。 - 因此,
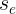 从另一角度说明了回归直线的拟合优度。
从另一角度说明了回归直线的拟合优度。
Q:计算不良贷款![]() 对贷款余额
对贷款余额![]() 回归的估计标准误差,并解释其意义?
回归的估计标准误差,并解释其意义?
A2:标准误差为1.9799,这就是说,根据贷款余额来估计不良贷款时,平均的估计误差为1.9799亿元。
得到估计回归方程后,是不是就能直接用来做预测了呢?还不能哦,因为该估计方程是根据样本数据得出的,它是否真实地反映了变量![]() 和
和![]() 之间的关系,需要通过检验来证实。那目前常用的检验方法有哪些?
之间的关系,需要通过检验来证实。那目前常用的检验方法有哪些?
回归分析中的显著性检验主要包括两个方面:线性关系的检验和回归系数的检验。
线性关系的检验是检验因变量![]() 与
与![]() 个自变量之间的关系是否显著,也称为总体显著性检验。
个自变量之间的关系是否显著,也称为总体显著性检验。
为检验自变量和因变量之间的线性关系是否显著,需要构造用于检验的统计量F。
如果原假设成立,则比值MSR/MSE的抽样分布服从分子自由度为![]() 、分母自由度为
、分母自由度为![]() 的F分布。
的F分布。
- 原假设:beta=0 (变量之间的线性关系不显著)
- 备择假设:beta!=0 至少有一个不等于0(变量之间的线性关系显著)
- 当原假设成立时,MSR/MSE的值应接近1;
- 当原假设不成立时,MSR/MSE的值将变得无穷大;
线性关系检验主要是检验因变量与多个自变量的线性关系是否显著, 在![]() 个自变量中,只要有一个自变量与因变量的线性关系显著,F检验就能通过,但这不一定意味着每个自变量与因变量的关系都显著。
个自变量中,只要有一个自变量与因变量的线性关系显著,F检验就能通过,但这不一定意味着每个自变量与因变量的关系都显著。
Q:检验不良贷款![]() 和贷款余额
和贷款余额![]() 之间线性关系的显著性(
之间线性关系的显著性(![]() )?
)?
A1:提出假设 ![]() (两个变量之间的线性关系不显著)
(两个变量之间的线性关系不显著)
A3:查F分布表,得临界值![]() 。由于
。由于![]() , 拒绝原假设
, 拒绝原假设 ![]() ,表明不良贷款和贷款余额之间的线性关系是显著的。
,表明不良贷款和贷款余额之间的线性关系是显著的。
A4:用于F检验的P值![]() ,拒绝原假设
,拒绝原假设 ![]() ,表明因变量和自变量之间有显著的线性关系。【备注:pf(Significance F)取值可看上图回归分析结果的pf取值。】
,表明因变量和自变量之间有显著的线性关系。【备注:pf(Significance F)取值可看上图回归分析结果的pf取值。】
回归系数的检验是检验自变量对因变量的影响是否显著。
回归系数检验是对每个回归系数分别进行单独检验,它主要用于检验每个自变量对因变量的影响是否显著。如果某个自变量没有通过检验,就意味着这个自变量对因变量的影响不显著,也许就没有必要将这个自变量放进回归模型中。
Q:检验回归系数的显著性(![]() )?
)?
A1:提出假设 ![]() (无显著关系);
(无显著关系); ![]() (有显著关系);
(有显著关系);
A3:查t分布表,得临界值![]() 。由于
。由于![]() , 拒绝原假设
, 拒绝原假设 ![]() ,这意味着贷款余额是影响不良贷款的一个显著因素。
,这意味着贷款余额是影响不良贷款的一个显著因素。
A4:用于t检验的P值P-value![]() ,拒绝原假设
,拒绝原假设 ![]() ,表明因变量和自变量之间有显著的线性关系。【备注:P-value取值可看上图回归分析结果的变量C对应P-value的取值。】
,表明因变量和自变量之间有显著的线性关系。【备注:P-value取值可看上图回归分析结果的变量C对应P-value的取值。】
注意:F检验只是用来检验总体回归关系的显著性,而t检验则是检验各个回归系数的显著性。
AIC准则即Akaike information criterion,又叫赤池准则,为日本统计学家赤池弘次创立,它建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。
AIC计算公式为: AIC=2k-2logLik,其中:k是参数的数量,logLik是对数似然比。
BIC准则即Bayesian Information Criterions,于1978年由Schwarz提出。BIC的惩罚项比AIC大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
BIC计算公式为: BIC=-2logLik +kln(n)。
AIC或BIC的取值是越小越好。