拿下红黑树
红黑树
- 红黑树、2-3树的简单定义:
- 实现红黑树的基本结构以及添加操作(维护定义,左旋、右旋、颜色反转)
- 红黑树与BST、AVL 的性能比较及总结;
1. 红黑树的简单定义:
1.1 基本特性
算法导论对红黑树的定义有一定弊端,上来直接看定义,会懵
1. 每个节点或者是红色的,或者是黑色的
2. 根节点一定是黑色的
3. 每一个叶子节点(最后的空节点)是黑色的,这个空节点不同于传统意义上左右子树都为空的节点;
4. 如果一个节点是红色的, 那么它的两个孩子节点都是黑色的
5. 从任意一个节点到叶子节点(同3定义),经过的黑色节点是一样的;
1.2 理解红黑树更好的一种方式 - 算法4
红黑树与2-3树的等价关系,理解2-3树和红黑树之间的关系
红黑树就很简单了
学习2-3树不仅对理解红黑树有帮助,对于理解B类树,也是有巨大帮助的:
1.3 2-3 树
1.3.1 2-3 树的特性:
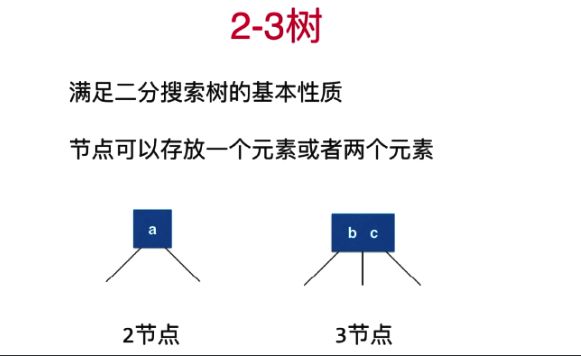
1. 满足二分搜索树的基本性质;
2. 不是二叉树
3. 节点可以存放1个或者2个元素
4. 每一个节点有2个或者3个孩子 - 2-3 树
所谓2 or 3 就看当前节点有多少个孩子
5. 2-3 树是一棵绝对平衡的树
绝对平衡树: 从根节点到任意一个叶子节点所经过的节点树是相同的
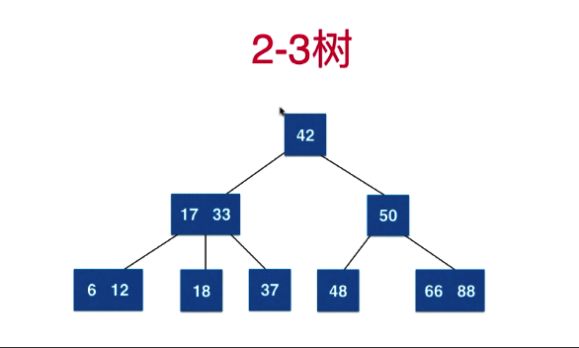
一棵完整的2-3树
1.3.2 2-3 树如何维持绝对的平衡
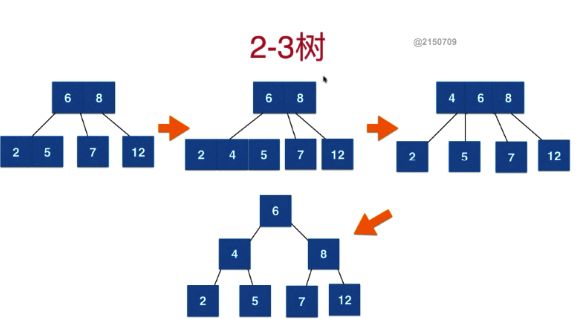
2-3树维持绝对平衡的步骤:
新入节点如果打破了2-3树的定义(入加入节点后节点中存储了>2个的元素),则中间节点上移成为根节点
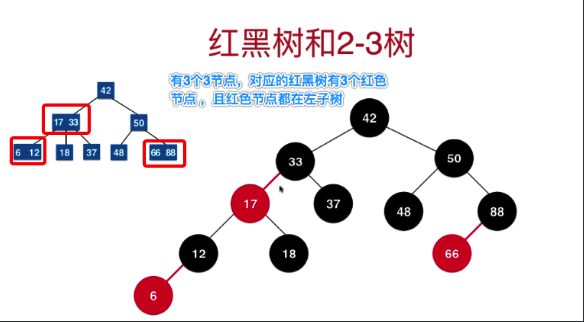
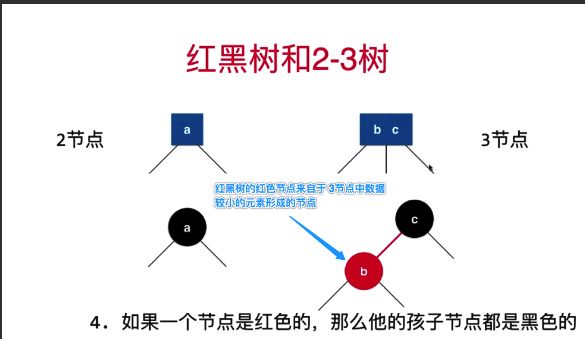
1.3.3 2-3树和红黑树是等价的
因为我们定义的树结构不会用具体的对象去定义节点连接的边,所以我们将3节点中的较小元素的节点用红色表示,其在较大元素节点的左边,并且表示为红色。
如下图所示:
红黑树中红色节点的由来:
红黑树不是AVL树,但是是保持黑平衡的二叉树(节点的左右黑子树高度差 <= 1)
1.3.4 红黑树的代码定义(对BST树进行改造)
1.3.4.1 定义红黑树的节点颜色
"""
# @Time : 2020/2/29 下午10:37
# @Author : [email protected]
# @Site :
# @File : RBTree.py
# @Software: PyCharm
手动实现红黑树
其实这里相当于用红黑树实现了一个HashMap,
先实现定义一下数据结构中的属性
"""
# 节点颜色, RED 为true, black 为False
RED = True
BLACK = False
class Node:
"""
定义了key->val 键值对
"""
def __init__(self, key=None, val=None, left=None, right=None):
self.key = key
self.val = val
self.left = left
self.right = right
# 节点颜色定义为 boolean 类型,True 代表红色、False
self.color = RED
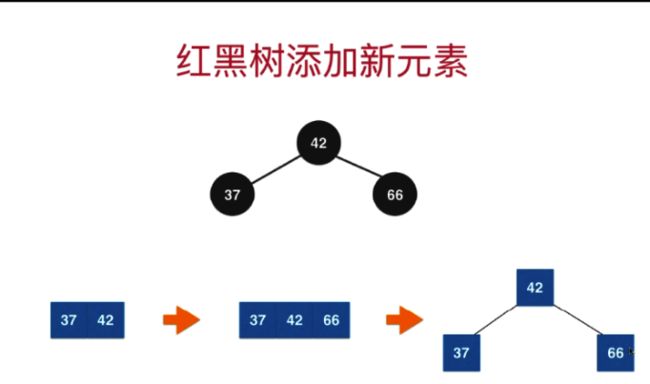
1.3.4.2 红黑树维持根节点为黑色 & 等价2-3树 中2节点的新增操作
转换过程:
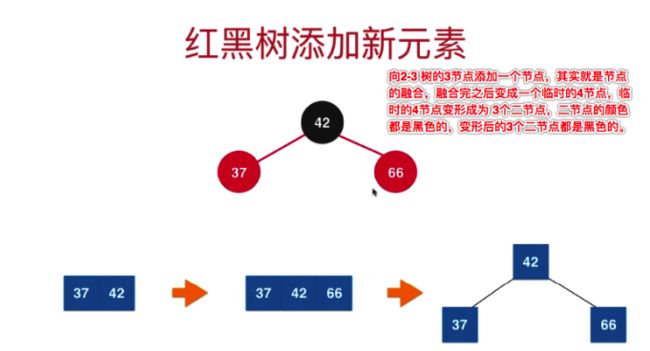
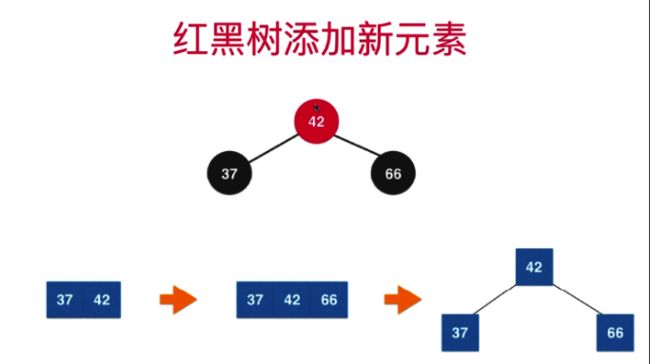
1.3.4.3 红黑树对应等价2-3树3节点融合(新增节点操作) 颜色反转与右旋转
场景1:新加元素的val比当前3节点的值都大
当前场景(新加入节点在当前节点的右侧)新增完节点后:
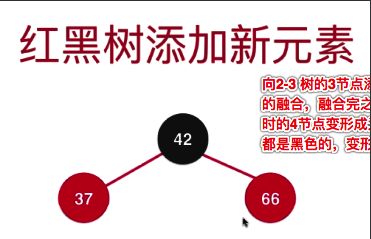
会发现变形完后的临时4节点会变为3个2节点,此时节点颜色都为黑色
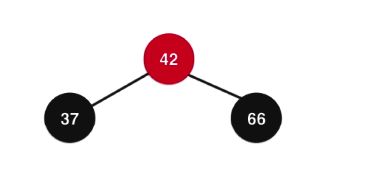
接下来当临时4节点变为3个2节点后,根节点需要继续向上融合,且当前根节点需要变为红色
最后我们发现待向上(与父亲节点)融合的根节点需要变为红色
其实这个过程就是颜色反转- flip_colors
如下图所示:
至
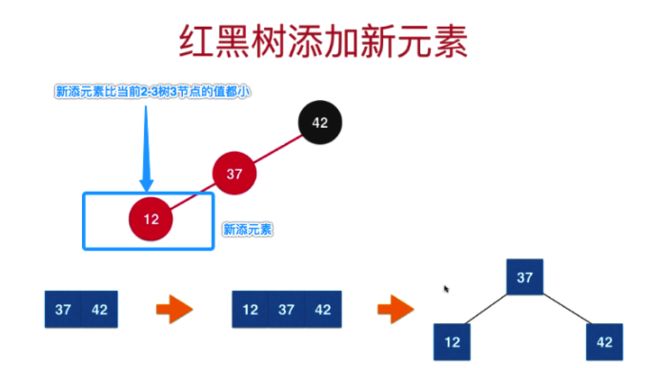
场景2:新加元素的val比当前3节点的值都小
如下图所示:
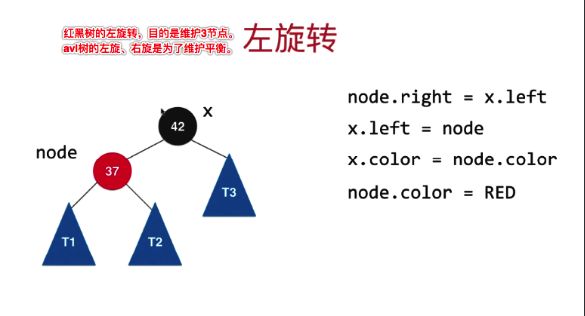
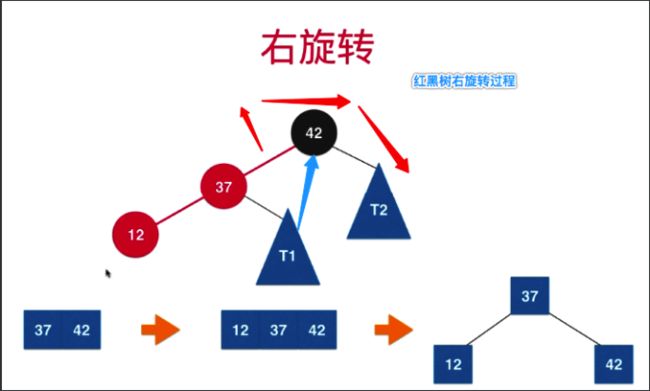
此时需要进行一个右旋转(对根进行旋转)
如下图所示:
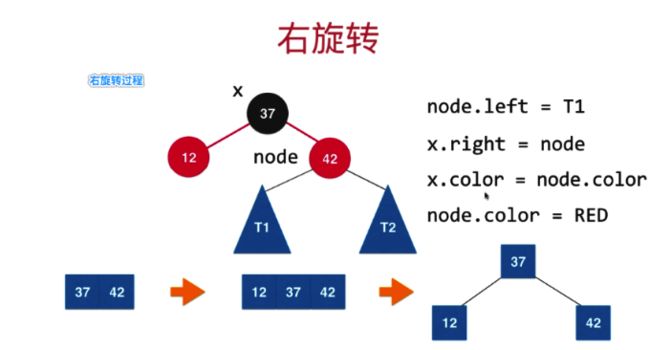
经过右旋转,变为如下形式:
之后再进行颜色反转就可以保证红黑树每一个红色节点的子树跟节点都为黑色的性质了。
其实会发现,x的节点颜色值跟原先根节点的颜色值保持一致,之后原先跟节点的颜色值变为红色,表示当前3个2节点对应临时的4节点。
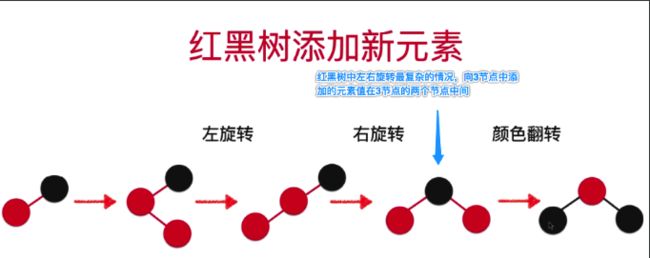
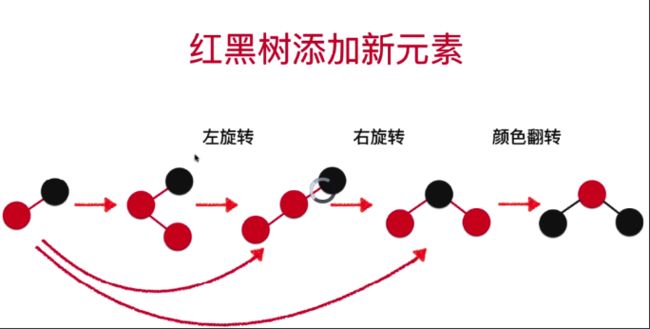
**场景3: 新加元素的val在当前3节点的中间
左 右 颜色反转
所以通过总结可以知道:
如下所示,我们最终实现的红黑树结构定义以及add元素操作
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
# @Time : 2020/2/29 下午10:37
# @Author : [email protected]
# @Site :
# @File : RBTree.py
# @Software: PyCharm
手动实现红黑树
其实这里相当于用红黑树实现了一个HashMap,
先实现定义一下数据结构中的属性
"""
# 节点颜色, RED 为true, black 为False
RED = True
BLACK = False
class Node:
"""
定义了key->val 键值对
"""
def __init__(self, key=None, val=None, left=None, right=None):
self.key = key
self.val = val
self.left = left
self.right = right
# 节点颜色定义为 boolean 类型,True 代表红色、False
self.color = RED
class RBTree:
def __init__(self):
self._root = None
self._size = 0
def get_size(self):
return self._size
def is_empty(self):
return self._size == 0
def is_red(self, node: Node):
"""
返回当前节点的颜色
:param node:
:return:
"""
if node is None:
return BLACK
return node.color
def _left_rotate(self, node: Node):
"""
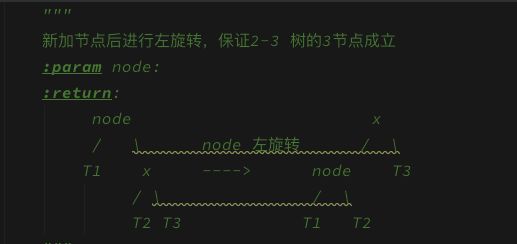
新加节点后进行左旋转,保证2-3 树的3节点对应红黑树的表示成立, 在我们的定义中, 红色节点均在父亲节点的左侧
:param node:
返回左旋转,对根节点的反转
:return:
node x
/ \ node 左旋转 / \
T1 x ----> node T3
/ \ / \
T2 T3 T1 T2
"""
x = node.right
node.right = x.left
x.left = node
# 维持节点颜色
x.color = node.color
node.color = RED
return x
def _flip_colors(self, node: Node):
"""
根据case进行调用
3节点融合-进行颜色反转 辅助函数
:return: 不返回任何节点,只需要改变节点颜色
"""
node.color = RED
node.left.color = BLACK
node.right.color = BLACK
def _right_rotate(self, node: Node):
"""
:param node:
:return:
node x
/ \ / \
x T2 --> 右旋转 y node
/ \ / \
y T1 T1 T2
"""
x = node.left
# 右旋转过程
node.left = x.right
x.right = node
x.color = node.color
# 与父亲节点x融合在一起
node.color = RED
return x
def add(self, key, val):
self._root = self._add_element(self._root, key, val)
# 保持跟节点为黑色
self._root.color = BLACK
def _add_element(self, root, key, val):
"""
向root为根的红黑树中插入元素(key, val) 使用递归算法
:param root:
:param key:
:param val:
:return: 返回新的红黑树的根
"""
if root is None:
self._size += 1
"""
返回的是子树根节点
"""
return Node(key, val)
elif key < root.key:
root.left = self._add_element(root.left, key, val)
elif key > root.key:
# insert
root.right = self._add_element(root.right, key, val)
else:
# or update
root.val = val
# 红黑树性质的维护
if self.is_red(root.right) and self.is_red(root.left) is False:
# case-0 2节点中新增一个比较大的值进行融合,则红色节点右偏移,则进行左旋转
root = self._left_rotate(root)
if self.is_red(root.left) and self.is_red(root.left.left):
# case-1 如果3节点中新增一个最小的值进行融合,则先进行右旋转,再进行颜色反转
root = self._right_rotate(root)
if self.is_red(root.left) and self.is_red(root.right):
# case-2 节点的左右子树的根节点都为红色,则进行颜色的反转,转化之后,红色节点的子树根节点都为黑色
self._flip_colors(root)
return root
2 红黑树与AVL、BST 之间的性能比较及差异
2.1 红黑树性能测试
红黑树相对于AVL树insert 和 remove 操作更有优势一点
3. 红黑树的性能总结
红黑树性能总结:
1. 对于完全随机的数据,普通的(BST)二分搜索树很好用! 会偏移
2. 对于查询比较多的时候,AVL树很好用 比较矮
3. 红黑树属于黑平衡,牺牲了平衡性,2log(n)的高度,所以查询相对AVL性能较弱
但是添加操作,会较AVL树更优一点。
TreeMap、TreeSet 底层是红黑树,
统计性能更优。
如下图所示: