推荐系统（五）Graph Convolution Network

本文尝试通过最简单易懂的语言来讲解GCN(Graph Convolution Network)原理，希望能够帮助大家理解GCN。这里只是讲解GCN的大致原理，公式细节上会省略一些常量，请大家见谅，毕竟这篇博客的目的在于GCN入门，不是深奥的数学知识。如果有讲的不对的地方，麻烦大家一定提出，毕竟错误的知识引导会造成无可估量的知识体系的伤害。

首先阐述一下一些CNN网络模型在图像领域的效果较好原因：网络不同层的卷积核在该层的输入数据上滚动能够提取到相应维度的特征，且通过不断的迭代从而学习到有效的提取特征方法，从而更好地完成任务。上述任务能够有效完成的前提是数据输入结构相对固定，具体而言，一个网络模型的输入是有要求的，比如说网络模型的输入格式为$128\ast 128\ast 3$，这个输入数据(通常为图像)的每个位置都必须有值。

但如果输入是结构不固定的数据，比如一个图，再利用CNN模型完成指定任务的难度就相对较大，因为这和CNN模型的本质是冲突的。针对上面的问题，GCN的解决方案直截了当，将输入结构不固定的数据转换为结构固定的数据，然后再送入CNN模型中，个人认为GCN完成的核心任务相当于CNN的数据预处理过程，只不过这个预处理过程和CNN以往的预处理有所不同，需要在CNN每层处理之前都要做一遍。

关键字： 傅里叶变换，拉普拉斯矩阵，切比雪夫多项式

如下是本篇博客的主要内容：

• GCN引入原因
• 从傅里叶变换到GCN
• 第一代GCN 原始拉普拉斯矩阵
• 第二代GCN 切比雪夫多项式的应用
• 第三代GCN 切比雪夫多项式的截断

---

1. GCN引入原因

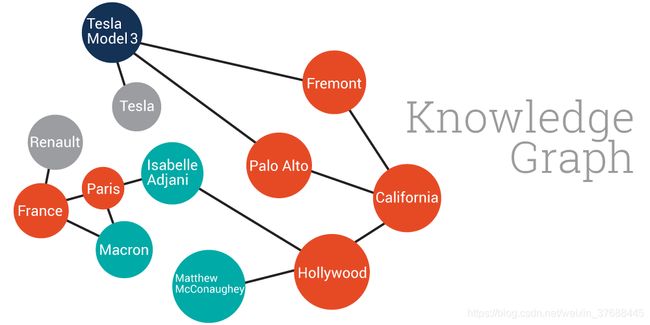
博客一开始提到一部分GCN被引入的原因，这里再具体阐述一下为什么CNN对于结构不固定的输入数据无能为力。这里举个例子，如果现在的任务是对节点的颜色进行预测，那么如果不对如下数据结构映射成一个固定的数据结构的话，则没有办法对其顺利地进行卷积操作，GCN所完成的正是这种映射。

2. 从傅里叶变换到GCN

2.1 傅里叶变换

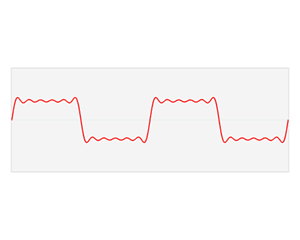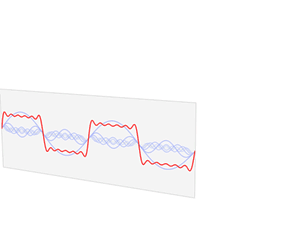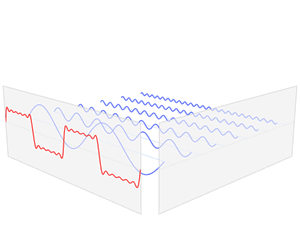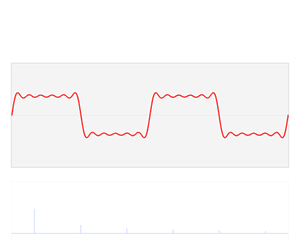
将一个不固定的数据结构或者信号映射(解析)成一个相对固定的结构或者信息，这就是傅里叶变换本身要解决的问题，其核心在于将信号的空间域转换为频域来表示，本来在空间域表现形式很复杂的信号，转换到频率却非常简单明了，其工作原理如下所示(时间较长，麻烦耐心看完)，

可以发现，一个复杂的波浪信号从空间域转换到频域，就变成了几个简单的尖峰。其具体的工作原理就是将一个复杂的信号分解为几个简单正交信号(傅里叶变换的基)的线性叠加，然后把这几个简单信号的振幅和频率提取出来，作为频域空间的$y$值和$x$值，假如上面信号公式如下，
$$f(t)=\frac{1}{2\pi }\int A_w{e}^{iwt}dw\approx \sum _j{A}_j{e}^{i{w}_{j}t}(1)$$

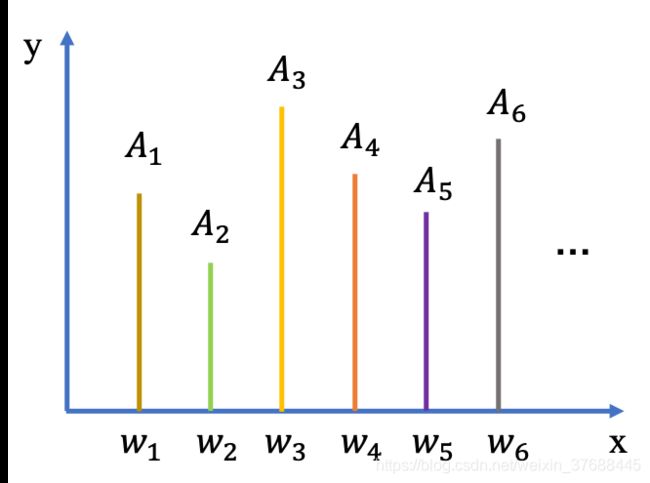
其频域的表示如下所示，

上述每个频率$w_j$上的振幅取值又可以通过原始空间域信号求解可得，公式如下，这里省略公式的证明，大家如果有兴趣可以参考傅里叶变换的具体原理介绍。

$$A_j=\hat{f}(w_j)=\int f(t)e^{-iwt}dt(2)$$

上面连续信号公式中积分符号比较难理解，我们将连续信号变为离散信号，公式如下，这里限定离散信号的维度为$M$，频域空间的维度为$N$，其中$u_j=\{u_1(1),u_1(2),...,u_1(M){\}}^T$为上述的第j个正交信号，
$$f(i)=\sum _{j=1}^N{A}_j{u}_j(i)(3)$$

将$M$维向量的公式展开计算如下，抽象化公式为$f=U\hat{f}$，
$$\left(\begin{array}{c}f(1)\\ f(2)\\ ...\\ f(M)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_2(1)& ...& u_N(1)\\ u_1(2)& u_2(2)& ...& u_N(2)\\ ...& ...& ...& ...\\ u_1(M)& u_2(M)& ...& u_N(M)\end{array}\right)=\left(\begin{array}{c}\hat{f}(w_1)\\ \hat{f}(w_2)\\ ...\\ \hat{f}(w_N)\end{array}\right)$$

其每个频率$w_j$上的振幅取值如下所示，这里的$u_j^{\ast }(i)$指的是$u_j(i)$的共轭，
$$A_j=\hat{f}(w_j)=\sum _{i=1}^{M}f(i)u_j^{\ast }(i)(4)$$

将$N$维向量的公式展开计算如下，抽象化公式为$\hat{f}=U^{T}f$，
$$\left(\begin{array}{c}\hat{f}(w_1)\\ \hat{f}(w_2)\\ ...\\ \hat{f}(w_N)\end{array}\right)=\left(\begin{array}{cccc}{u}_1^{\ast }(1)& u_1^{\ast }(2)& ...& u_1^{\ast }(M)\\ u_2^{\ast }(1)& u_2^{\ast }(2)& ...& u_2^{\ast }(M)\\ ...& ...& ...& ...\\ u_N^{\ast }(1)& u_N^{\ast }(2)& ...& u_N^{\ast }(M)\end{array}\right)=\left(\begin{array}{c}f(1)\\ f(2)\\ ...\\ f(M)\end{array}\right)$$

2.2 GCN理论

从2.1节中的描述可以看出如果能找到傅里叶变换的基$\{u_j{\}}_{j=1}^N$，就能唯一搭建空间域到频域之间的桥梁。现在将目光转向当前的GCN问题，假设当前已知一个图$G=(V,E)$，其中总共有$N$个节点，每个节点的取值为$f(i)$，每个节点的label为$l_i$，这时要学习一个模型，使模型的预测值尽量准，那么如果依然采用CNN卷积提取特征并预测的方式，会因上文所说的结构不固定而难度较大。

GCN的做法是将卷积操作在数据结构固定的"频域"内完成，因而现在问题的关键在于找到傅里叶变换的基$\{u_j{\}}_{j=1}^N$，这些基需要保证是相互正交的，因而这里科学家就采用图的拉普拉斯矩阵这个一贯被使用的概念(虽然有些牵强，但是在很多博客上确实是这么说的…)，并将拉普拉斯矩阵的特征向量作为频域的基来进行求解，且频域中每个频率$w_j$对应到拉普拉斯矩阵的特征值${\lambda }_j$。

这里简单讲下拉普拉斯矩阵，假设图$G$的邻接矩阵为$A$，邻接矩阵的度矩阵为$D$，则拉普拉斯矩阵为$L=D-A$，拉普拉斯矩阵的两个比较常见的变种为：1. 随机游走归一化拉普拉斯矩阵$L^{rw}=D^{-1}L$，2. 对称归一化拉普拉斯矩阵$L^{sym}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}$，而后GCN采用的拉普拉斯矩阵为$L^{sym}$，原因是大家都在用(原因依然很牵强…)。这里再提一点，因为图中的节点个数为$N$，因而$L^{sym}$的维度为$N\times N$，因而上文所说的离散信号的维度$M$和频域空间的维度$N$是相同的，这里都用$N$来表示。

根据上述基本知识的铺垫，正式开始讲述GCN的工作原理。首先GCN的卷积是在频域上完成的，具体来说，就是将原始的输入$f$映射到频域变为$\hat{f}$，原始的卷积核$h$映射到频域变为$\hat{h}$，$\hat{f}$和$\hat{h}$卷积完成之后，再将输出反映射到空间域，相当于在空间域完成卷积操作，从而达到和CNN一样的效果，公式如下所示，这里${\mathbb{F}}^{-1}$代表的是傅里叶反变换。
$$f\ast h={\mathbb{F}}^{-1}[\hat{f}(\lambda )\ast \hat{h}(\lambda )]$$

其中$\widehat{h({\lambda }_j)}={\sum }_{j=1}^{N}h(j)u_j^{\ast }(i)$，根据上文的$\hat{f}=U^{T}f$可得：
$$\hat{f}(\lambda )\ast \hat{h}(\lambda )=\left(\begin{array}{ccc}\widehat{h({\lambda }_1)}& & \\ & ...& \\ & & \widehat{h({\lambda }_n)}\end{array}\right)U^{T}f(5)$$

又根据上文的$f=U\hat{f}$可得如下公式，即GCN每一层的输出。
$$f\ast h=U\left(\begin{array}{ccc}\widehat{h({\lambda }_1)}& & \\ & ...& \\ & & \widehat{h({\lambda }_n)}\end{array}\right)U^{T}f(6)$$

3. 第一代GCN 原始拉普拉斯矩阵

第一代GCN直接将公式(6)中的对角矩阵作为参数来学习，而后添加上激活函数就变为了一层神经网络的输出，即
$$y=\sigma (U\Lambda (\theta )U^{T}x)(7)$$
其中$\Lambda (\theta )$为如下公式，
$$\Lambda (\theta )=\left(\begin{array}{ccc}{\theta }_1& & \\ & ...& \\ & & {\theta }_N\end{array}\right)(8)$$

这时可以看出该方法有一个显而易见的缺点，就是计算量太大，先不管矩阵分解，只是矩阵的连续相乘就有$O(n^2)$的时间复杂度，而且参数的个数为$N$，这两个特点对于庞大的网络来说都是没办法接受的，但是我个人觉得参数的大小并不是一个特别大的问题，因为下面几个方法的参数都不小…

4. 第二代GCN 切比雪夫多项式的应用

对于第3节提出方法的缺点，科学家们提出了另一个想法，即如下公式，其中$T_k(\Lambda )$是$\Lambda$的多项式，即切比雪夫多项式，
$$\Lambda (\theta )=\sum _{k=0}^K{\theta }_k{T}_k(\Lambda )(9)$$

但是这样做的前提是$\Lambda$的定义域为[-1,1]，因而需要对$\Lambda$进行变换，即如下公式，这时就能保证切比雪夫多项式能应用到这里，
$$\tilde{\Lambda }=\frac{2\Lambda }{{\lambda }_{max}}-I_N$$
进而公式(9)变为如下公式，
$$\Lambda (\theta )=\sum _{k=0}^K{\theta }_k{T}_k(\tilde{\Lambda })(9)$$
这里切比雪夫多项式另外的性质如下所示：
$$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)(10)$$

其中$T_0(x)=I,T_1(x)=x$，这里再套用公式(7)得到如下公式，
$$y=\sigma (U\sum _{k=0}^K{\theta }_k{T}_k(\tilde{\Lambda })U^{T}x)(11)$$

又由于$T_k(\tilde{\Lambda })$是$\tilde{\Lambda }$的多项式，且$U{\tilde{\Lambda }}^k{U}^T=(U\tilde{\Lambda }{U}^T{)}^k={\tilde{L}}^k$，其中$\tilde{L}=\frac{2L^{sym}}{{\lambda }_{max}}-I_N$，因而公式(11)可变为如下公式，
$$y=\sigma (U\Lambda (\theta )U^{T}x)=\sigma (U\sum _{k=0}^K{\theta }_k{T}_k(\tilde{\Lambda })U^{T}x)=\sigma (\sum _{k=0}^K{\theta }_{k}U{T}_k(\tilde{\Lambda })U^{T}x)=\sigma (\sum _{k=0}^K{\theta }_k{T}_k(\tilde{L})x)$$

这样做的好处在于算法的时间复杂度虽然进一步降低，但这里依然要算${\tilde{L}}^k$，因而时间复杂度依然为$O(n^2)$，而且参数量并没有减少，因为这里的${\theta }_k$是一个矩阵，而不是$\Lambda (\theta )$中的一个取值，但该算法带来的一个好处即spatial localization，即如果K=1，卷积的含义为每个顶点上一阶neighbor的feature进行加权求和，如下图所示，

如果K=2，则需要将更远的二阶neighbor的feature做加权平均，如下图所示，

5. 第三代GCN 切比雪夫多项式的截断

这里可以对第4节中的公式做进一步简化，即K=1，${\lambda }_{max}=2$则有如下公式，

$$y=\sigma ([{\theta }_0+{\theta }_1(L^{sym}-I_N)]x)=\sigma ([{\theta }_0-{\theta }_1{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}]x)$$

而如果令${\theta }_0=-{\theta }_1=\theta$，则有$y=\sigma (\theta (I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})x)$，但实际应用中会遇到另一个问题，即梯度爆炸，因为公式中每次都会添加一个$I_N$，因而这里做了一个trick，
$$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$
其中$\tilde{A}=A+I_N$，$\tilde{D}$为$\tilde{A}$的度矩阵，神经网络的最终输出为
$$y=\sigma (\theta {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}x)$$

这就是kipf在其博客上晒出的公式。

到这里，本文就把GCN的来龙去脉讲了个大概，其实大家要想真正了解其如何实现的，还是要去看作者的源码，这样才能对GCN的原理有进一步的认识。

参考

1. 如何理解 Graph Convolutional Network（GCN）
2. Chebyshev多项式作为GCN卷积核
3. 图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯)
4. GRAPH CONVOLUTIONAL NETWORKS