如何使用threejs实现第一人称视角的移动

在数据可视化领域利用webgl来创建三维场景或VR已经越来越普遍，各种开发框架也应运而生。今天我们就通过最基本的threejs来完成第一人称视角的场景巡检功能。如果你是一位threejs的初学者或正打算入门，我强烈推荐你仔细阅读本文并在我的代码基础之上继续深入学习。因为它将是你能够在网上找到的最好的免费中文教程，通过本文你可以学习到一些基本的三维理论，threejs的api接口以及你应该掌握的数学知识。当然要想完全掌握threejs可能还有很长的路需要走，但至少今天我将带你入门并传授一些独特的学习技巧。

第一人称视角的场景巡检主要需要解决两个问题，人物在场景中的移动和碰撞检测。移动与碰撞功能是所有三维场景首先需要解决的基本问题。为了方便理解，首先需要构建一个简单的三维场景并在遇到问题的时候向你演示如何解决它。

 1 
 2 
 3 
 4     
 5     
 6     
 7     
 8 
 9 
10 
11 
12 
98 

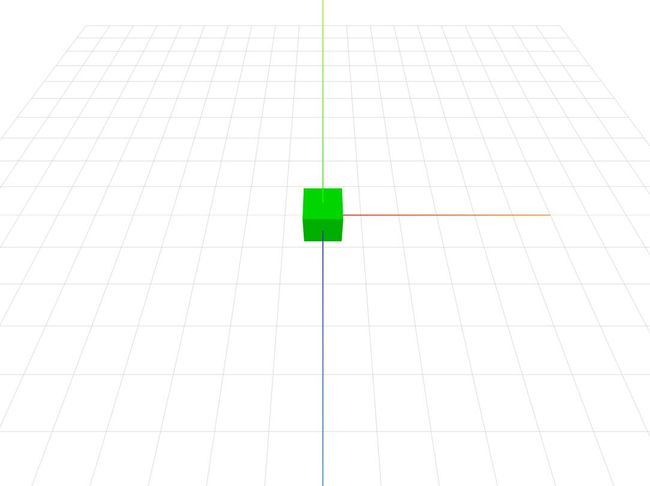
很多js的开发人员非常熟悉jquery，我引用它确实让代码显得更加简单。首先我在init()方法里初始化了一个场景。我知道在大部分示例中包括官方提供的demo里都是通过threejs动态的在document下创建一个节点。我强烈建议你不要这样做，因为在很多单页面应用中（例如：Vue和Angular）直接操作DOM都不被推荐。接下来我使用helper()方法创建了两个辅助对象：一个模拟地面的网格和一个表示世界坐标系的AxesHelper。最后我利用createBoxer()方法在视角中央摆放了一个绿色的立方体以及绑定了三个鼠标动作用来控制立方地旋转。如图：

 

你可以尝试将代码复制到本地并在浏览器中运行，移动鼠标看看效果。接下来，为了让方块移动起来，我们需要添加一些键盘响应事件，以及给方块的“正面”上色。

  1 
  2 
  3 
  4     
  5     
  6     
  7     
  8 
  9 
 10 
 11 
 12 
154 

 

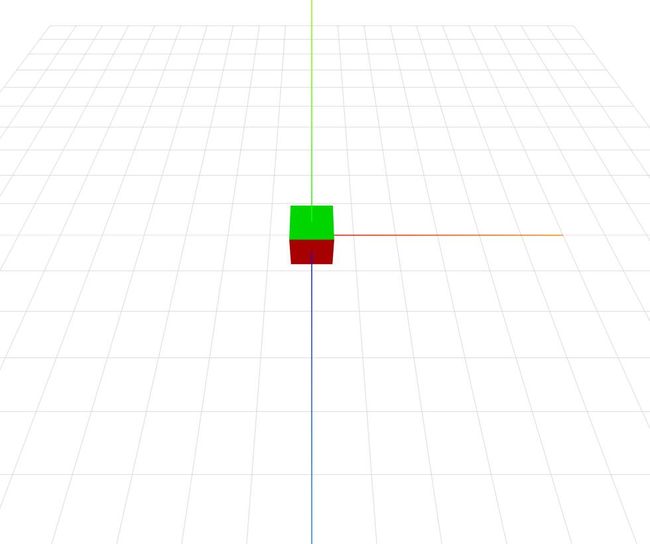
我们添加了keydown()事件和keyup()事件用来捕获键盘响应。我们还修改了createBoxer()方法，给朝向我们的那一面涂上红色。你一定发现了BoxGeometry所代表的立方体虽然只有6个面，可是为了给“1个面”上色我们却需要同时在“2个面”的材质上着色。这是因为在三维场景中，“面”的含义表示由空间中3个点所代表的区域，而一个矩形由两个三角形拼接而成。完成以后的样子如下：

随意拖动几下鼠标，我们可能会得到一个类似的状态：

设想一下在第一人称视角的游戏中，我们抬高视角观察周围后再降低视角，地平线是否依然处于水平状态。换句话说，无论我们如何拖动鼠标，红色的那面在朝向我们的时候都不应该倾斜。要解释这个问题，我们首先需要搞清楚三维场景中的坐标系概念。在threejs的世界中存在两套坐标体系：世界坐标系和自身坐标系。世界坐标系是整个场景的坐标系统，通过它可以定位场景中的物体。而自身坐标系就比较复杂，实际上一个物体的自身坐标系除了用来表示物体各个部分的相对关系以外主要用来表示物体的旋转。想象一下月球的自转和公转，在地月坐标系中，月球围绕地球公转，同时也绕着自身的Y轴旋转。在我们上面的场景中，立方体自身的坐标轴会随着自身的旋转而改变，当我们的鼠标自下而上滑动后，Y轴将不再垂直于地面。如果这时我们再横向滑动鼠标让立方体绕Y轴旋转，自然整个面都会发生倾斜。如果你还不理解可以在自己的代码中多尝试几次，理解世界坐标系和自身坐标系对于学习webgl尤其重要。很显然，要模拟第一人称的视角转动我们需要让视角上下移动的旋转轴为自身坐标系的X轴，左右移动的旋转轴固定为穿过自身中心的一条与世界坐标系Y轴保持平行的轴线。理解这个问题很不容易，可是解决它却非常简单。threejs为我们提供了方法，我们只需要修改mousemove()方法：

$(window).mousemove(function (event) {
        event.preventDefault();
        if (leftPress) {
            cube.rotateOnWorldAxis(
                new THREE.Vector3(0, 1, 0),
                event.originalEvent.movementX / 500
            );
            cube.rotateOnAxis(
                new THREE.Vector3(1, 0, 0),
                event.originalEvent.movementY / 500
            );
        }
    });

有了控制视角的方式，接下来我们移动一下方块。新的问题又出现了：盒子的运动方向也是沿着自身坐标系的。就和我们看着月亮行走并不会走到月亮上去的情形一样，如果要模拟第一人称视角的移动，视角的移动方向应该永远和世界坐标系保持平行，那么我们是否可以通过世界坐标系来控制物体的移动呢：

 1  function animate() {
 2         requestAnimationFrame(animate);
 3         renderer.render(scene, camera);
 4         if (front) {
 5             // cube.translateZ(-1)
 6             cube.position.z -= 1;
 7         }
 8         if (back) {
 9             // cube.translateZ(1);
10             cube.position.z += 1;
11         }
12         if (left) {
13             // cube.translateX(-1);
14             cube.position.x -= 1;
15         }
16         if (right) {
17             // cube.translateX(1);
18             cube.position.x += 1;
19         }
20     }

很显然也不行，原因是我们应该让物体的前进方向与物体面对的方向保持一致：

尽管这个需求显得如此合理，可是threejs似乎并没有提供有效的解决方案，就连官方示例中提供的基于第一人称的移动也仅仅是通过固定物体Y轴数值的方法实现的。在射击游戏中不能蹲下或爬上屋顶实在不能让玩家接受。为了能够在接下来的变换中分解问题和测试效果，我们在模型上添加两个箭头表示物体的前后方向。

 1 let arrowFront, arrowBack;
 2 
 3 function animate() {
 4         requestAnimationFrame(animate);
 5         renderer.render(scene, camera);
 6         arrowFront.setDirection(cube.getWorldDirection(new THREE.Vector3()).normalize());
 7         arrowFront.position.copy(cube.position);
 8         arrowBack.setDirection(cube.getWorldDirection(new THREE.Vector3()).negate().normalize());
 9         arrowBack.position.copy(cube.position);
10         if (front) {
11             // cube.translateZ(-1)
12             cube.position.z -= 1;
13         }
14         if (back) {
15             // cube.translateZ(1);
16             cube.position.z += 1;
17         }
18         if (left) {
19             // cube.translateX(-1);
20             cube.position.x -= 1;
21         }
22         if (right) {
23             // cube.translateX(1);
24             cube.position.x += 1;
25         }
26     }
27 
28 function createBoxer() {
29         var geometry = new THREE.BoxGeometry(5, 5, 5);
30         var mats = [];
31         mats.push(new THREE.MeshPhongMaterial({color: 0x00ff00}));
32         mats.push(new THREE.MeshPhongMaterial({color: 0xff0000}));
33         cube = new THREE.Mesh(geometry, mats);
34         for (let j = 0; j < geometry.faces.length; j++) {
35             if (j === 8 || j === 9) {
36                 geometry.faces[j].materialIndex = 1;
37             } else {
38                 geometry.faces[j].materialIndex = 0;
39             }
40         }
41         scene.add(cube);
42         arrowFront = new THREE.ArrowHelper(cube.getWorldDirection(), cube.position, 15, 0xFF0000);
43         scene.add(arrowFront);
44         arrowBack = new THREE.ArrowHelper(cube.getWorldDirection().negate(), cube.position, 15, 0x00FF00);
45         scene.add(arrowBack);
46     }

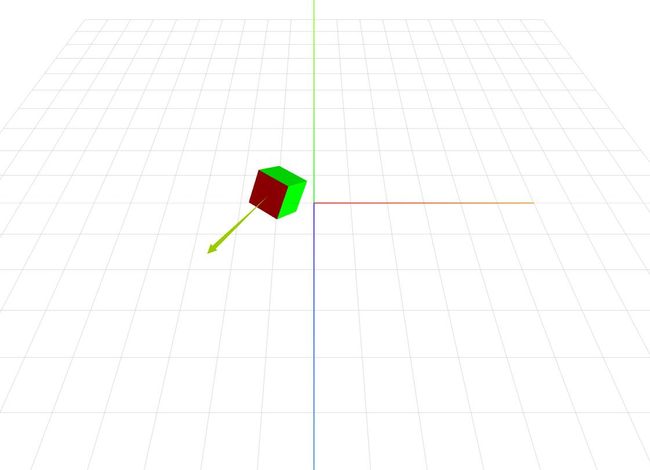
修改后的效果如下：

有了箭头的辅助，我们能够以比较直观的方式测试算法是否有效。如果你能够认真读到这里，可能已经迫不及待想继续了，但是还请稍安勿躁。进入下个环节前，我们需要首先了解几个重要的概念。

1. 三维向量（Vector3）：可以表征三维空间中的点或来自原点（0,0,0）的矢量。需要注意，Vector3既可以表示空间中的一个点又可以表示方向。因此为了避免歧义，我建议在作为矢量的时候通过normalize()方法对向量标准化。具体api文档参考。
2. 欧拉角（Euler）：表示一个物体在其自身坐标系上的旋转角度，欧拉角也是一个很常见的数学概念，优点是对于旋转的表述相对直观，不过我们在项目中并不常用。
3. 四元数（Quaternion）：四元数是一个相对高深的数学概念，几何含义与欧拉角类似。都可以用来表征物体的旋转方向，优点是运算效率更高。
4. 四维矩阵（Matrix4）：在threejs的世界中，任何一个对象都有它对应的四维矩阵。它集合了平移、旋转、缩放等操作。有时我们可以通过它来完成两个对象的动作同步。
5. 叉积（.cross() ）：向量叉积表示由两个向量所确定的平面的法线方向。叉积的用途很多，例如在第一人称的视角控制下，实现左右平移就可以通过当前视角方向z与垂直方向y做叉积运算获得：z.cross(y)。
6. 点积（.dot()）：与向量叉积不同，向量点积为一个长度数据。vect_a.dot(vect_b)表示向量b在向量a上的投影长度，具体如何使用我们马上就会看到

在理解了上面的概念以后，我们就可以实现沿视角方向平移的操作：我们知道，物体沿平面（XOZ）坐标系运动都可以分解为X方向上的运动分量和Z轴方向上的运动分量。首先获取视角的方向，以三维向量表示。接着我们需要以这个向量和X轴方向上的一个三维向量做点积运算，从而得到一个投影长度。这个长度即代表物体沿视角方向移动的水平x轴方向上的运动分量。同理，我们在计算与Z轴方向上的点积，又可以获得物体沿视角方向移动的z轴方向的运动分量。同时执行两个方向上的运动分量完成平移操作。

接下来，我们先通过实验观察是否能够获得这两个运动分量和投影长度。

  1 
  2 
  3 
  4     
  5     
  6     
  7     
  8 
  9 
 10 
 11 
 12 
178 

 

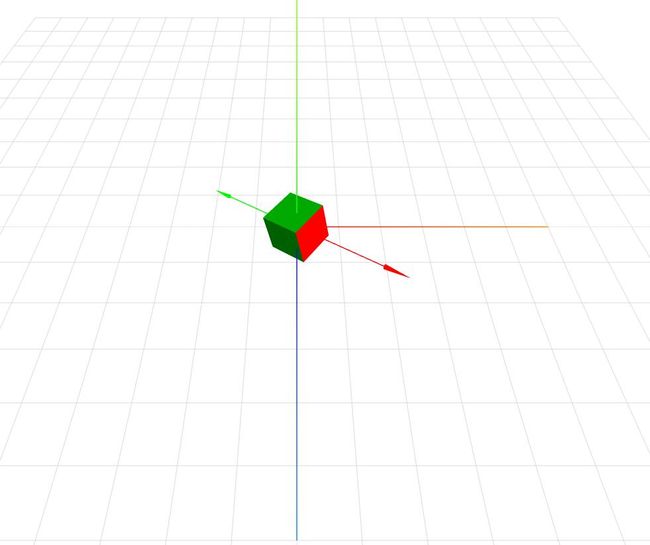
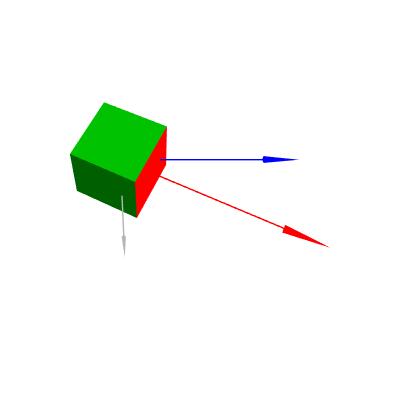
通过箭头的辅助，我们很容易获得以下图形：

红色箭头表示物体的朝向，蓝色表示物体沿x轴上的投影方向和长度。灰色表示沿z轴上的投影方向和长度。在确认方法可行以后，我们继续实现平移操作。完整代码如下，这个运算的方式很重要，读者应该仔细比较两段代码的差别。

  1 
  2 
  3 
  4     
  5     
  6     
  7     
  8 
  9 
 10 
 11 
 12 
151 

向后和左右平移的操作留给大家自己实现。有了以上基础，如何控制Camera移动就很简单了。几乎就是将cube的操作替换成camera即可：

  1 
  2 
  3 
  4     
  5     
  6     
  7     
  8 
  9 
 10 
 11 
 12 
129 

解决了平移操作以后，碰撞检测其实就不那么复杂了。我们可以沿着摄像机的位置向上下前后左右六个方向做光线投射（Raycaster），每次移动首先检测移动方向上的射线是否被阻挡，如果发生阻挡且距离小于安全距离，即停止该方向上的移动。后面的部分我打算放在下一篇博客中介绍，如果大家对这篇文章敢兴趣或有什么建议欢迎给我留言或加群讨论。

转载于:https://www.cnblogs.com/learnhow/p/11565596.html