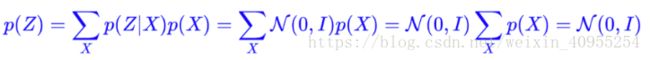VAE全面理解（下）

在上一篇中，我自认为用浅显的语言向诸位介绍了VAE的整个发展的过程，在这篇中，将较多的涉及框架构建以及公式推导部分。

那么，开始吧

1）框架构建

首先我们有一批数据样本 x1,…,xn}，其整体用 X 来描述，我们本想根据 {x1,…,xn} 得到 X 的分布 p(X)，如果能得到的话，那我直接根据 p(X) 来采样，就可以得到所有可能的 X 了（包括 {x1,…,xn} 以外的），这是一个终极理想的生成模型了。但是，这个过程往往是很困难的。

于是，我们退而求其次，就想到了上文中提到的隐形变量Z，这个Z就是决定最终x形态的因素向量。给定一个图片Xk，我们假定p(Z|Xk)是专属于Xk的后验概率分布，这个概率分布服从正态分布。得到了这个概率，我们可以从分布中采样，并且通过最终的解码器将图片再恢复出来。

由于上述所说，我们所假设的这些分布都是正态分布，那么我们就需要求得相应的方差和均值，所以在编码实现的过程中，不难看到encoder部分真实做的事情就是，对相应的输入数据，通过两个网络产生了均值和方差。

那么，我们再次思考一下接下来的训练过程，我们的目的是使重构之后的图片与输入的图片之间的差距越小越好。但是在这重构在引入均值方差以及之后的高斯分布的时候，是引入了噪声的，也就是说为了提高模型的准确性，这个高斯分布的方差最后将收敛为零，而在这个时候，模型也就失去了生成的效果，无法生成新的图片。

那怎么办呢，别急，还记得之前VAE的一个假设嘛？p(Z|Xk)是服从高斯分布的。所以，通过下面这个公式的计算，我们可以求得Z的分布：

这样的话，Z的分布就会保持在标准正态分布，从而保证了生成器可以继续生成。

最终我们的VAE的框架图可以表达成下图所示;

理解了这部分的原理，再次跟着我回到原理讲解部分对应着原理讲解在理解一次VAE吧

2）公式推导

在上述框架中我们希望的到的p(z|x)并不好求，所以有人就提出来使用变分的方法构建一个q(z|x)来近似p(z|x)。同时在这里利用KL三都来衡量两个分布之间的距离。

因为对于P(x)，它的值是固定的，所以为了最小化分布q(z|x)和p(z|x)之间的距离，需要最大化这个Lv，也被称为最大变分下限。而经过推导又可以得到：

因为最大变分下限需要最大化，所以他推到之后的绿色框和红色框，首先这两个值是相互独立的，然后我们需要最下化绿框中不带负号的值，也就是说要让q（z/x）和p（z）这两个分布尽可能的接近。我们一般都会假设z是服从高斯分布的，所以这里的q分布也需要近似服从高斯分布。

这里解释一下，这个q就是在上文系统框架中的编码器部分，对于他生成的均值和方差，我们可以看出这个q是服从高斯分布的。

同时呢，上框中的红色部分也是需要最大化的，这个红色部分对应的是解码器部分，即要求在训练过程中，回构出来的图像要尽量的与输入的图像相同。

3）reparametrization trick

在实际应用过程中，为了做backpropagation，（如下面左边的图中，z的值是一个随机变量，所以在反向传播过程中我们没有办法计算对z导数）我们通常用reparametrization trick代替randomly sample，（即通过引入一个高斯分布e，将z变成一个确定的值，从而使得反向传播可以得以计算）具体过程如下：（图中圆圈代表随机变量，方块代表变量的值是确定的）

 

参考：

在写这两篇博客的过程中，我大量参考了以下这几篇文章，但是觉得他们又都各有侧重，所以将他们综合了一下重新写了出来。感谢这些博主的无私分享，我会更努力的。。。。。

1、VAE(Variational Autoencoder)的原理

2、https://www.jeremyjordan.me/variational-autoencoders/

3、读论文《Auto-Encoding Variational Bayes》

4、变分自编码器VAE：原来是这么一回事 | 附开源代码

我是钱多多，一个刚刚开始研究僧生涯的小菜鸟，欢迎大家交流指正。

学术交流可以关注我的公众号，后台留言，粉丝不多，看到必回。卑微小钱在线祈求