BST树的插入、删除、查询操作
目录
- 1.什么是BST树
- 2.BST树的节点
- 3.BST树的插入操作
- 非递归插入
- 递归插入
- 4.BST树的删除操作
- 非递归删除
- 递归删除
- 5.BST树的查询操作
- 非递归查询
- 递归查询
1.什么是BST树
二叉搜索树(Binary Serach Tree),又称二叉排序树,其简写为BST树。对于二叉树上的每一个节点,如果满足左孩子的值 < 父节点的值 < 右孩子的值,那么就称这棵二叉树为二叉搜索树。
例如:
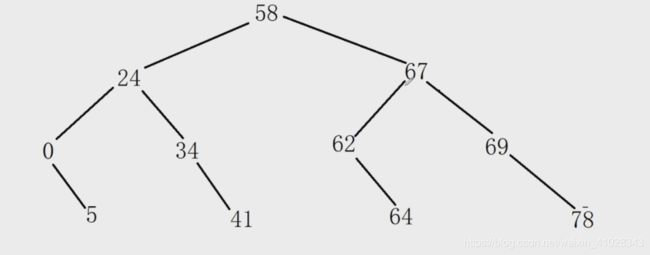
在这棵二叉树中,对于每一个节点均满足左孩子 < 父节点 < 右孩子。
2.BST树的节点
BST的树的节点与普通的二叉树一样,节点中存储当前节点的值以及两个指向左右孩子的指针域。如下:
template<typename T>
struct Node
{
Node(T data = T())
:_data(data)
,_left(nullptr)
,_right(nullptr)
{}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
3.BST树的插入操作
非递归插入
向BST树中插入一个节点,有以下两种情况:
- 该树为一个空树,即第一个插入的节点。
- 该树不为空。
针对第一种情况,如果插入的是该树的第一个节点,那么root直接指向新生成的节点即可。如果为第二种情况,那么此时应该利用BST树左孩子 < 父节点 < 右孩子 的性质,从根节点开始进行比较,找到合适的位置,生成新的节点,并把新节点的地址写入父节点相应的地址域中。
代码如下所示:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
void insert(const T& data)
{
//判断是否为空树
if(nullptr == _root)
{
//把新生成的节点赋给_root
_root = new Node(data);
return;
}
//如果树不为空,搜索插入位置
Node* cur = _root; //比较节点
Node* parent = nullptr; //记录插入位置的父节点,以便后续将待插入节点写入其父节点的地址域
while(cur!=nulllptr)
{
//如果当前节点的值等于待插入节点的值,直接return
if(cur->_data == data)
{
//不允许插入相同元素
return;
}
//如果当前节点的值小于待插入节点值,则向当前节点的右子树遍历
else if(cur->_data < data)
{
parent = cur;
cur=cur->_right;
}
//如果当前节点的值大于待插入节点值,则向当前节点的左子树遍历
else
{
parent=cur;
cur=cur->_left;
}
}
//找到待插入位置,生成新节点,并将新节点的地址写入父节点相应的地址域中
//如果父节点的值小于待插入节点值,则将待插入节点的地址写入父节点的右孩子域中
if(parent->_data < data)
{
parent->_right = new Node(data);
}
//如果父节点的值大于待插入节点值,则将待插入节点的地址写入父节点的左孩子域中
else
{
parent->_left = new Node(data);
}
}
private:
struct Node
{
Node(T data = T())
:_data(data)
,_left(nullptr)
,_right(nullptr)
{}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};
递归插入
采用递归进行插入时,我们需要提供用户的插入接口,以及内部用于实现递归的接口,出于C++的封装特性,一般将实现递归的函数置为私有成员。递归分为两步,第一步是向下递归,目的是为了给待插入节点寻找合适的插入位置,第二步是向上回溯,目的是将新生成的节点的地址域写入父节点的相应的地址域中。
代码如下所示:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
//用户调用接口
void r_insert(const T& data)
{
_root = r_insert(_root, data);
}
private:
struct Node
{
Node(T data = T())
:_data(data)
, _left(nullptr)
, _right(nullptr)
{}
//用于递归的接口
Node* r_insert(Node* node, const T& data)
{
//递归结束条件:如果树为空树或者找到合适的插入位置
if (nullptr == node)
{
return new Node(data);
}
//如果重复插入,则直接返回已插入节点的地址
if (node->_data == data)
{
return node;
}
//向下递归:寻找插入位置
//向上回溯:把孩子节点的地址写入父节点相应的地址域中
//node->_data < data:当前节点的值小于待插入节点的值,向当前节点的右子树递归
if (node->_data > data)
{
node->_right = r_insert(node->_right, data);
}
//node->_data > data:当前节点的值大于待插入节点的值,向当前节点的左子树递归
else
{
node->_left = r_insert(node->_left, data);
}
}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};
4.BST树的删除操作
非递归删除
删除BST树中的某一个几点,会有以下3种情况:
- 待删除节点没有孩子。
- 待删除节点有一个孩子。
- 待删除节点有两个孩子。
对于第一种情况,因为待删除节点没有孩子,直接将其父节点的地址域置空即可;对于第二种情况,因为其只有一个孩子,删除节点后直接将其孩子的地址写于父节点相应的地址域即可;
但是对于第三种情况,因为待删除节点有两个孩子,如果直接删除,你无法知道将其两个孩子节点如何安置,所以此处不能直接删除,此处可以使用待删除节点的前驱节点或者后继节点(前驱和后继节点下文具体描述)的值直接将待删除节点的值覆盖掉,然后再删除其前驱节点或者后继节点即可,根据前驱节点和后继节点的特性,就可将问题转换为第一种或者第二种情况。
前驱节点:当前节点左子树中值最大的节点(左子树的最右节点)。
后继节点:当前节点右子树中值最小的节点(右子树的最左节点)。
前驱节点和后继节点的特性:只有一个孩子或者没有孩子。
所以在删除节点时,优先处理第三种情况,因为第三种情况最终将会转换为第一种或第二种情况。
此处还有一点需要注意:如果待删除节点为根节点并且根节点只有一个孩子时,那么在删除时直接去删除根节点的话,根节点是没有父节点的,所以没法将孩子节点的地址写入到父节点的地址域种,此时处理方法为直接将根节点的孩子节点置为根节点。如下述情况:
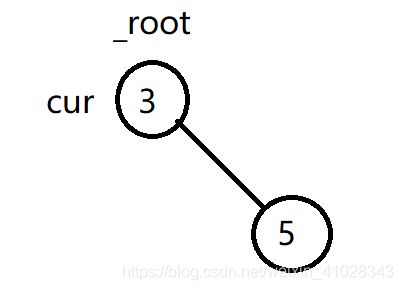
代码:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
void remove(const T& data)
{
//判断是否为空树,如果为空树,就不存在删除节点这一说了
if(nullptr == _root)
{
//直接返回即可
return;
}
//树不为空,搜索待删除节点
Node* cur = _root; //搜索节点
Node* parent = nullptr; //记录待删除节点的父节点,以便后续将待删除节点孩子的地址写入其父节点的地址域
while(cur!=nullptr)
{
//找到待删除节点,停止搜索
if(cur->_data == data)
{
break;
}
//如果当前节点的值小于待删除节点的值,则继续向其右子树遍历
else if(cur->_data < data)
{
parent = cur;
cur = cur -> _right;
}
//如果当前节点的值大于待删除节点的值,则继续向其左子树遍历
else
{
parent = cur;
cur = cur -> _left;
}
}
//如果当前节点为空,则表示这颗BST树中不存在该待删除节点
if(nullptr == cur)
{
return;
}
//如果不为空,那么cur即为待删除节点
//优先处理第3种情况:待删除节点有两个孩子
if(cur->_left != nullptr && cur->_right != nullptr)
{
//此处以前驱节点为例,前驱节点:左子树的最右节点
//寻找待删除节点的前驱节点,并用前驱节点的值直接覆盖待删除节点的值,把问题转换为情况1或者情况2
parent = cur;
Node* prev = cur -> _left;
//搜索前驱节点
while(prev->_right != nullptr)
{
parent = prev;
prev=prev->_right;
}
//用前驱节点的值覆盖待删除节点
cur->_data = prev->_data;
//让cur指向前驱节点,将问题转化为情况1或者情况2
cur=prev;
}
//此时cur指向待删除节点,parent指向待删除节点的父节点,统一处理情况2和情况3
//此处如果为情况1,即没有孩子,那么child始终为空,如果有孩子,那么child将指向其孩子
Node* child = cur->_left;
if(nullptr == child)
{
child = cur->_right;
}
//特殊情况:如果只有两个节点,并且待删除节点为根节点
if(cur==_root)
{
//直接将其孩子置为根节点
_root = child;
}
//非特殊情况
//把待删除节点的孩子地址写入父节点相应的地址域
else
{
if(parent->_left == cur)
{
parent->_left = child;
}
else
{
parent->_right = child;
}
}
//删除待删除节点
delete cur;
}
private:
struct Node
{
Node(T data = T())
:_data(data)
,_left(nullptr)
,_right(nullptr)
{}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};
递归删除
采用递归删除某一节点时,思路与非递归的思路一致,仍然是要针对三种情况做出处理,并且优先处理第三种情况。与递归插入相同,同样要实现用户调用接口以及用于的递归接口,也是非两步进行,第一步是向下递归寻找待删除节点,找到后按照非递归中处理三种情况的逻辑进行处理;第二步是向上回溯,把删除节点的孩子写入父节点的相应的地址域中。
代码如下所示:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
//用户调用接口
void r_remove(const T& data)
{
_root = r_remove(_root, data);
}
private:
struct Node
{
Node(T data = T())
:_data(data)
, _left(nullptr)
, _right(nullptr)
{}
//用于递归的接口
//向下递归:寻找待删除节点
//向上回溯:将待删除节点的孩子写入父节点相应的地址域中
Node* r_remove(Node* node, const T& data)
{
//如果为空树或者未找到待删除节点,直接返回空
if (nullptr == node)
{
return nullptr;
}
//如果树不为空
//找到待删除节点
if (node->_data == data)
{
//优先处理情况3
if (node->_left != nullptr && node->_right != nullptr)
{
//寻找前驱节点
Node* pre = node->_left;
while (pre->_right != nullptr)
{
pre = pre->_right;
}
//修改待删除节点的值,转换为情况1或者情况2
node->_data = pre->_data;
//通过递归直接删除前驱节点,因为前驱节点为原待删除节点的左子树中的节点,
//所以以左子树为根,转化为情况1或者情况2,更新左子树的孩子域
//注意:此时待删除的节点已经转化为前驱节点了,所以传值的时候要传前驱节点的值
node->_left = r_remove(node->_left, pre->_data);
}
//情况1或者情况2
else
{
//左孩子存在
if (node->_left != nullptr)
{
Node* left = node->_left;
delete node;
return left;
}
//右孩子存在
else if (node->_right != nullptr)
{
Node* right = node->_right;
delete node;
return right;
}
//左右孩子均不存在
else
{
delete node;
return nullptr;
}
}
}
//node->_data < data:当前节点的值小于待删除节点的值,向当前节点的右子树递归
else if (node->_data < data)
{
node->_right = r_remove(node->_right, data);
}
//node->_data > data:当前节点的值大于待删除节点的值,向当前节点的左子树递归
else
{
node->_left = r_remove(node->_left, data);
}
}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};
5.BST树的查询操作
非递归查询
BST树的查询较为简单,根据BST树的定义可知,其每一个节点均满足:左孩子 < 父节点 < 右孩子,所以查询某一个节点是否在该BST树中时,从根节点开始开始比较,如果当前节点的值小于所查询节点的值时,就继续在当前节点的右子树中比较;如果当前节点的值大于所查询节点的值时,就继续在当前节点的左子树中比较;如果当前节点的值等于所查询节点的值时,查找结束。
代码:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
bool query(const T& data)
{
//首先判断是否为空树,如果为空树,也就没有查询某节点这一说了
if(nullptr == _root)
{
return false;
}
//从根节点开始比较
Node* cur = _root;
while(cur!=nullptr)
{
//如果当前节点的值等于所查询节点的值时,查找结束
if(cur->_data == data)
{
return true;
}
//如果当前节点的值小于所查询节点的值时,就继续在当前节点的右子树中比较
else if(cur->_data < data)
{
cur=cur->_right;
}
//如果当前节点的值大于所查询节点的值时,就继续在当前节点的左子树中比较
else
{
cur=cur->_left
}
}
//没有查询到
return false;
}
private:
struct Node
{
Node(T data = T())
:_data(data)
,_left(nullptr)
,_right(nullptr)
{}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};
递归查询
采用递归进行查询时,思路与非递归相同,根据BST树的性质进行查询即可。
代码如下所示:
template<typename T>
class BST
{
public:
BST()
:_root(nullptr)
{}
//用户调用接口
bool r_query(const T& data)
{
return nullptr != r_query(_root, data);
}
private:
struct Node
{
Node(T data = T())
:_data(data)
, _left(nullptr)
, _right(nullptr)
{}
//用于递归的接口
Node* r_query(Node* node, const T& data)
{
//如果树为空或者node走到空时,表示未查询到,返回空
if (nullptr == node)
{
return nullptr;
}
//查询到待查询节点
if (node->_data == data)
{
return node;
}
//node->_data < data:当前节点小于待查询节点的值,向当前节点的右子树进行递归
else if (node->_data < data)
{
return r_query(node->_right, data);
}
//node->_data < data:当前节点大于待查询节点的值,向当前节点的左子树进行递归
else
{
return r_query(node->_left, data);
}
}
T _data;
struct Node* _left; //左孩子域
struct Node* _right; //右孩子域
};
Node* _root;
};