【数据结构与算法】【课程设计】公园的导游图系统

↓以下为不重要的废话↓ 我已经对我们学校的课设无力吐槽了，别人都是线性表，到我这直接上来一个导游图。
如果后来的学弟学妹在找课设的时候看到这篇，请多改一改再拿去用，因为别人的报告都二三十页，这个打出来会有七十页。（附录我没放这，当时完整代码都在附录里足足有142页，老师都震惊了。）
检查报告的时候，老师说别人不都一二百行代码吗，可简单了，我当时就想把导游图拍他头上，一个图类就要四百多行好吗！（当然也可能是我想的太多）有时间我会把文件换成数据库的……
代码在文章资料里，不放了，太长了……
或者可以去github【https://github.com/RayChang-CN/mischief】 ↑废话结束↑

1.设计目的

1.1课题内容及意义

本次课程设计遵循一般软件生存周期，采用自顶向下的设计思路、面向对象的思想和基于建模的分析方法，从实际情况及需求出发，设计实现了公园导游图系统。此系统交互性较好，可根据使用权限的不同管理某公园内各景点及景点间路线长度，或查询与之有关的信息。在对系统内信息进行管理时对数据进行了较好的封装，安全性和可扩展性较高，可以实现对公园内各景点及景点间路径的存在和路径长度的创建或更新，并能根据需要给出某两个景点间的最短路径和环游整个公园的最优路线。
处理的问题涉及图模型的建立和使用、单源最短路径问题遗迹旅行商问题，涉及到Dijstr算法、回溯和分支限界算法，简单处理了相关数据在数据文件中的存储和使用。是对相关内容所涉及的数据结构、程序设计、算法分析相关课程内容的综合利用和整合。
在具体的设计过程中，逐步建立问题模型并围绕软件生存周期设计系统，从问题分析入手，找到相关问题的解和得出该解的算法，验证该算法的正确性并尝试优化算法。随后根据问题，逐步建立需求、数据、概念和设计的相关模型，并完成功能测试。最终得到具有良好的交互性、可扩展性及复用性且安全性较好的系统。

1.2相关术语及符号表示

1.图、顶点、边：几何上将空间一些点（顶点）和连接这些点的线（边）构成的集合定义为图。图论中将其定义为一个偶对G=(V,E)，其中，V表示顶点的集合，E表示边的集合。

2.权值、度、道路：若顶点u、v间有边相连，则可表示为e=。e长度称为该边上的权值，表示为|e|=||。设|e|=w(e)即可将带权图表示为G=(V,E;w)。从顶点v出发的边的数目称为v的度，记为d(v）。设顶点和边的交替序列

且两端顶点分别为边的两端点为一条道路。本文中为方便表述，省去边e，用有边相连的顶点表示道路，即μ=，其中分别是E中的边。

3.回路、哈密顿回路：若对上述道路μ，∈E，则称μ为一回路。若图G中存在一条道路P，它通过每一个顶点各一次，则称P为图G 的哈密顿回路，亦称哈密顿环、哈密顿圈。

4.哈密顿环定理：设简单图G=（V,E;w）的顶点数为n，(n＞3)。若对G中至少一对顶点u∈V，v∈V恒有d(u)+d(v)≥n-1，则图G中至少有一条哈密顿回路。

5.角色、用例、系统：本文中系统指与此次课程设计相关的所有软件部分的整体，包括控制模块和数据文件模块两部分。角色是系统额外部实体，为系统提供输入或者响应系统输出。用例用文字叙述形式描述角色与系统之间的交互，在下文中，遵循统一建模语言（UML）的规定，将角色、用例、系统和其关系如图1-1所示表示。

图1-1 简单用例图表示

6.实体、关系：数据文件中将实体（entity）定义为具有相同属性且区别于他物的现实存在，即对现实事物的抽象，某类实体的特定对象成为实体实例。在不涉及数据文件的上下文其他部分中，实体可作相同定义，但更关注其所代表的现实事物在系统中的作用。UML中将关系定义为下条所述几种，用以表示各角色、用例、类、实体中间的联系。数据文件用关系表示两个实体间的联系，仅在第五章中应用此种定义。

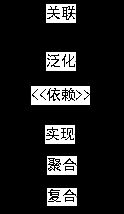
7.泛化、实现、关联、聚合、组合、依赖：泛化归纳不同元素间的一般性和特殊性，表现为父类和子类中的继承关系；实现体现在某类实现了接口的特征时；关联是基于对象实现各种类间的引用关系，这种引用关系使得某些类熟悉其他类的内部属性与方法；聚合和组合都体现在整体和局部的特殊关联，但组合中的局部类不能脱离全局类独立存在，依赖描述两个类中一个类的概念变化影响另一个类的概念发生变更。在下文中，这些关系可用不同的箭头表示，或用“<<关系>>”来标记，如图1-2所示。

图1-2 五种关系图例

1.3软件环境

系统环境：Windows 7；
编程环境：Eclipse Luna；
编程语言标准：JDK 13。

2.问题分析

2.1问题来源

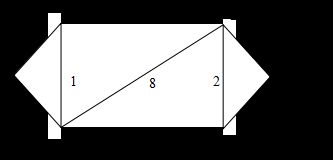
已知某公园导游图如图2-1所示，其中a，b，c，d，e，z分别为该公园中的几个景点，出入口均在a附近，各个景点间的道路长度标记为图中两景点间的数字。对公园中的游客，希望公园的管理方能提供这样的路线，使得他们不重复地走完公园中的所有景点且耗费最少的路线（此处的耗费可定义为该路线的长度），同时希望知道其中任意两个景点间的耗费虽少的路线。同时，若公园可以对导游图的信息加以维护，需要任意给定导游图中的各种信息作为输入，重新做上述处理，给出相应结果。

图2-1 某公园导游图

2.2问题抽象

一般而言，对任意的导游图，设此导游图中有n个景点v0，v1…vn-1，景点间有m条路e0，e1…em-1，若则可设此导游图为G=（V,E;w）,其中顶点集、边集分别为：

由图2-1可知，在此问题中，显然n=6，m=9。但如果只针对当前情况解决问题，当该公园的景点和道路情况发生变动，则需要重新设计解决方法。为能更一般地解决此问题，并为公园的管理方提供对应于实际情况中景点或道路变动信息改变的处理方式，则需先将导游图中的信息存储在计算机中，并提供给管理方针对这些信息的管理办法，再找到合适的算法，解决上述用户需要找到的两种路线。由此，本次课设需解决的问题包括：
（1）导游图G=（V,E;w）的表示（输入）与存储。
（2）对给定u∈V，v∈V，求，使得其长度最小。
（3）对给定v∈V，求从v出发通过其他所有顶点的回路和其上路径长度和

使得其长度和最小。
其中，问题（2）、（3）分别为图论中的单源最短路径问题和旅行商问题。

2.3可行性研究

2.3.1图的表示

对图G=(V,E;w)，构造矩阵

其中 则可用A表示其上所有顶点间的连通性及其权值。计算机中可以使用矩阵、数组或表来处处理矩阵A，则可设计一二维数组对应于该矩阵，并将其信息存储在文件或者数据库中，并设计对于该文件或数据库的处理接口以供使用。

2.3.2旅行商问题

根据哈密顿环定理，需要提醒公园方在构建景点及道路时加以限制，从而保证存在一条符合需要的环游路线。在程序处理中，则需要输入的导游图中的数据加以限制，即可以找到至少一条能经过图中所有顶点一次并回到原点的回路。
若已保证存在这样的哈密顿环，在搜索时对V中所有顶点做全排列，可能找到(n-1)!/2种方案。显然，随着n值的不断增大，问题将变得难以计算。已证明旅行商问题属于NPC问题，即不存在实际意义上的最优解，但仍可以找到其在一定条件下的最优近似解。
对V中所有顶点，设可得到其关于G-v的最小生成树T，设C是G的一个最优哈密顿环，显然C-v是G-v的一棵生成树，因此w(T)≤w(C-V)，设G中与v关联的且权最小和权次小的两边分别为e和f，则w(T)+w(e)+w(f)≤w©，因此w(T)+w(e)+w(f)即为G最优哈密顿环的下界估计式，若能找到算法使得找到的解接近这一估计，即为相对最优解。
在此条件下，设

是G的一个哈密顿圈，若存在一对i，j适合1＜i+1＜j＜p，并且 则一定存在新的哈密顿环

（由C中删去

再添加

而得到的），且其权和更小。即： 显然若存在这样的

其满足上述相对最优解的条件，则只需先找到上述回路C。由此，可规定：

则求回路C的步骤如下：
（1）任选u∈V，找与其关联且权最小的边e=作为路的开始部分；
（2）设已找出路，在V中取与最近的相邻顶点，得到；
（3）若i+1＜w(G)-1，令i=i+1,重复（2），否则，终止。
对旅行售货员问题，其解空间是一棵有排列树，直接遍历所有节点的时间耗费过大。实际应用时只需要找到某个特定的解，即可以达到要求。则可通过采用回溯法对其解空间树进行递归搜索。执行时通过判断能否构成哈密顿环以及当前耗费是否优于已找到的最优耗费，判断是否对当前解进行更新。可在O(N!)的时间耗费内完成计算。或者采用优先队列、最小堆能结构搜索其解空间树，当某个界定上的耗费不足以构成最优耗费，或者不能构成一条回路时，则处死该节点，以减小算法的时间复杂度。

2.3.3单源最短路径问题

如果对图G=(V,E)的任意两个顶点u与v，G中存在一条路,则称G是连通图，否则称为非连通图。由实际意义可知，导游图必然是联通的，则对任意两顶点，一定至少存在一条路使得其相连。当此路有且仅有一条时，这条路就是所求的最短路，当有多条路存在时，使其权值之和最小的一条路，即为所求的最短路径。由此，可以设置顶点集合S ，不断地选择使S中权值之和最小且能使得S中的起始顶点与目的顶点有边可达的顶点扩充集合S，当到达目的节点时，所得即为所求的最短路径，亦即求由源顶点到目的顶点的Dijkstra算法。
为证明此算法可得到所求最短路径，需证明其可通过局部最优解得到整体最优解，即Dijkstra算法满足贪心选择性质。同时需证明原问题可分解为相同规模的子问题且子问题的解可合并为原问题的解，亦即满足最优子结构性质。
为证其贪心选择性质，不妨设由此算法得到的最小值为D[u]，若存在从v到u的更短路径，设改路经过S之外的顶点x∈V-S，再经过其他路径到达u，则D[x]≤，同时可知||+||=||＜D[u]，又||≥0，可推得D[x]＜D[u]，产生矛盾，则在由此算法得到的解之外，不存在当前意义下的更优解。
为证明其最优子结构性质，只需观察每次向S中添加新顶点u构成新集合S’时，D[u]相对D[v]所发生的变化。顶点u可能生成到达目的顶点i的新路径，若此路经S到达u后直接到达i，则此路径的最短长度为D[u]+||。此时，若D[u]+||＜D[i]，则可用此值作为D[i]的新值。若此路径不能直接到达i，而是经S中某顶点x后再到达i，则根据算法步骤，x应比u先一步加入S中，故||＜||+||，则可推出D[i]＜||+||，即不需考虑此种路径，亦即D[u]的值在任何情况下都是当前顶点集S到u的最短路径的长度。
Dijkstra算法的执行过程可如图2-2中（1）到（8）的顺序所示，设要找从a景点到z景点间的最短路径，则以a景点为集合中的首元素，将不能直接到达的所有景点的距离置为无穷，每次将找到的最短的直接相连的景点添加进解集当中，直到到达z景点。
如果对图2-1中的导游图执行Dihjstra算法，其具体过程可由图2-2中（1）到（8）的过程所示。初始化整张图后，每次若将该节点加入解集，则用方框标注，每个节点旁边的数字标记了当前到该节点的最短路径长度和该路径在到达当前节点前经过的其他节点。

图2-2 Dijkstra算法执行过程

3.需求分析

本章的目标是确定系统中使用的数据、功能性需求和非功能性需求。其中，在基本功能需求中建立用例模型，用角色和用例描述系统的功能性需求，给出每个用例的叙事性描述，在此过程汇总，用户输入和主动参与是不可缺少的因素。

3.1数据需求

由2.2节的分析可知，本系统的后台主要关注与图模型有关的各种数据信息，而用户则关注实际景点的相关信息，因而系统需要处理的数据包括景点的名称、个景点间是否有道路相连以及道路的长度或耗费。此外，由2.3.1可知，需要在构建使用邻接表的图模型对道路是否相连和道路长度加以处理。则在图模型中，可设置一二维整型数组用以储存道路信息，其中行、列的下标分别为景点名称的编号以简化处理，若两景点间有道路，则将表中对应位置的值设置为该道路的长度。若无边相连，则将该长度设置为-1。由2.3.2节和2.3.3节的分析可知，为保证图中任意两节点间均有单源最短路径存在，并使得整个图的哈密顿环存在，需要对图中的数据加以处理。由此，在对整个图模型初始化的时候，需要对输入的数据加以处理，使得其满足存在单源最短路径和哈密顿环的条件。

3.2基本功能需求

3.2.1角色分析

角色是系统额外部实体，为系统提供输入或者响应系统输出。则在定义系统涉及到的角色时，首先应考虑系统中的可能涉及到的输入和输出。对整个系统而言，提供输出和响应输入的都应为使用该系统的人类角色，即刻抽象为“用户”这一角色。对需要使用不同功能的用户进一步细分，可将系统用户分为管理员和普通游客两种角色。其中管理员可以输入公园内各景点的数据并对其加以管理和维护，普通游客则只能选择查找某两个景点间的最短路径，或者环游整个公园的最短路线。而在系统内部，由于其流程控制模块和数据文件模块也产生交互关系，即在流程控制模块中收集原始数据，处理后输入给数据文件模块，数据文件模块中则准备好将输出的数据，输入给流程控制模块，在流程控制模块中最终输出。由此，可将流程控制模块抽象为“控制器”角色。

3.2.2用例分析

在用例模型中，用角色和用例定义系统的功能性需求。用例模型把系统视为一个黑箱，用文字叙述形式描述角色与系统之间的交互，关注系统在外部角色输入数做了什么而非系统内部如何去做。根据上文的分析，可抽象出七个用例，如下文所示。

3.2.2.1系统初始化用例

这一用例发生在整个对整个公园的导游图进行初始化或者要生成新的导游图时，将现实世界中的各种信息存储在计算机中。

---

用例名：创建导游图。
摘要：输入景点信息。
角色：管理员用户。
前置条件：景点信息为空或选择生成新表。
主序列：
（1）输入景点个数；
（2）输入出口和入口；
（3）依次输入各景点名；
（4）输入有路可达的两景点及此路径的长度；
（5）检查数据是否可用，若不可用，重新执行此序列。
非功能性需求：
可用性需求：满足图连通条件，具有哈密顿环。
后置条件：生成导游图的邻接表。

---

3.2.2.2修改导游图用例

如果需要对现有的导游图进行信息的修改，则执行如下用例。

---

用例名：修改导游图。
摘要：修改导游图信息。
角色：管理员用。
前置条件：已有导游图、
主序列：
（1）输入要执行的修改；
（2）选择修改的对象；
（3）判断修改后的数据是否可用，若不可用，重输。
非功能性需求：
（1）安全性需求
删除和修改时不能破坏图的连通性，也不能破坏哈密顿环。
（2）可用性需求
增加后满足图的连通性定理和哈密顿环存在定理。
后置条件：得到新图的邻接表。

---

3.2.2.3查找路径用例

游客在使用系统查找某两个景点间的最短路径时，需要根据提示输入两个景点，由系统输出其最短路径。

---

用例名：查找路径。
摘要：生查询两景点最短路径。
角色：游客用户。
前置条件：导游图中有数据。
主序列：
（1）选择查找路径功能
（2）输入起始景点；
（3）输入目的景点；
（4）输出最短路径。
非功能性需求：
安全性需求：结束后不改变原表中数据的值。
后置条件：生成包含环游整个公园路线的表。

---

3.2.2.4查找环游路线用例

游客在使用系统查找环游整个公园的最短路径时，由系统直接输出所需的最短路径。

---

用例名：查找环游路线。
摘要：查询整个公园的环游路线。
角色：游客。
前置条件：导游图中有数据。
主序列：
（1）选择查找路径功能
（2）输出环游路线。
非功能性需求：
安全性需求：结束后不改变原表中数据的值。
后置条件：生成包含环游整个公园路线的表。

---

3.2.2.5数据文件初始化用例

系统初始化用例得到数据后，控制器将数据处理并输入数据文件，得到关于导游图信息的数据文件。

---

用例名：初始化数据文件。
摘要：创建关于导游图信息的数据文件。
角色：控制器。
前置条件：系统初始化用例发生。
主序列：
（1）根据控制器提供的景点个数创建邻接表和最短路径表。
（2）将控制器提供的邻接关系存入邻接表。
（3）将控制器提供的最短路径和最优环游路线存入表中。
非功能性需求：
安全性需求：只有拥有管理员权限才能创建数据文件。
后置条件：生成包含公园各种路线信息的表。

---

3.2.2.6更新数据文件用例

控制器发出指令，对数据文件中的信息加以更新。
用例名：更新数据文件。

---

摘要：更新关于导游图信息的数据文件。
角色：控制器。
前置条件：存在导游图信息数据文件。
主序列：
（1）找到控制器要更新的景点。
（2）更新邻接表中的相应信息。
（3）根据控制器提供的最短路径和最优环游路线更新相关表。
非功能性需求：
安全性需求：只有拥有管理员权限才能更新数据文件。
后置条件：生成包含公园各种路线信息的表。

---

3.2.2.7查找景点数据用例

控制器发出指令，查找指定的景点信息并输出。

---

用例名：查找数据。
摘要：查找并输出关于导游图信息的数据文件。
角色：控制器。
前置条件：存在导游图信息数据文件。
主序列：
（1）找到控制器要更新的景点。
（2）找到该景点的相应信息。
（3）将相应信息输出给控制器。
非功能性需求：
安全性需求：查找不能改变数据文件中有的数据。
后置条件：生成包含公园各种路线信息的表。

---

3.3 非功能需求

用户界面需求：简洁、易用、易懂、友好的用户界面。
硬件要求：装有JVM的计算机。
可靠性需求：保证用户在正常使用本系统时，用户的操作或误操作不会产生数据的丢失。
安全性需求：只有管理员用户能对导游图中的信息进行修改，保证数据安全。

3.4小结

本章分析得到了使用此系统的角色并建立起与角色相关的用例模型，由上述分析可知，在公园导游图系统中，存在人类角色“用户”和软件角色“控制器”两类角色。其中，根据可使用功能的不同产生“管理员”和“游客”两类用户，控制器实质上由系统内部的控制模块产并处理数据文件模块的相关功能。整合各用户及用例间的依赖关系，可得如图3-1所示的用例图。

图3-1 系统用例图

4.概要设计

本章中定义系统的静态模型，即定义问题域中类之间的结构关系。用对象构造标准确定分析模型中所要考虑的对象。完成静态模型后，进一步开发动态交互模型，实现需求模型中的用例，显示每个用例所涉及的对象，以及这些对象之间的相互作用。用交互图、序列图或通信图描述。本章主要建立系统中涉及的各静态模型，抽象出其对象并建立类图。本章中涉及到的程序的帮助文档见附录一，相关源码见附录二。

4.1数据结构

根据上文中的分析，系统主要处理的数据对象为一个使用邻接表组成的图模型，此外，在旅行商算法中，还需要使用一个以旅行商算法中最小耗费为优先级的最小堆。遵循面向对象中封装、继承、多态的思想和工厂的设计模式，在本次的设计中，将这两种数据结构分别封装为一个类，其中分别包含与其有组合和聚合依赖关系的子类对象，其具体设计分别见5.1.1和5.1.2.2。

4.2各类间时序关系

利用上述设计得到的各个类完成并实现第三章的用例图，可以得到如图4-1和图4-2所示的时序图，其中的界面部分将在5.3节介绍。图4-1显示了用户角色的时序图，其实现了第三章的用例3和用例4。当用户向系统发出寻路请求时，系统通过激活选择界面给出响应，在接下来的通讯中，由用户选择自己所需的功能，并根据系统所给出的提示提示进行进一步操作。根据第四章所述的面向对象的原则，可以将每个对象封装成一个类，通过该类的构造析构调用其他相关类，从而完成整个调转和交互的过程。因而以下所述的界面均为独立的类，但在其类体中只提供调用其他方法的入口，该界面类本身并不执行功能。从而实现在第三章中将控制器作为角色的抽象。

图4-1用户角色时序图
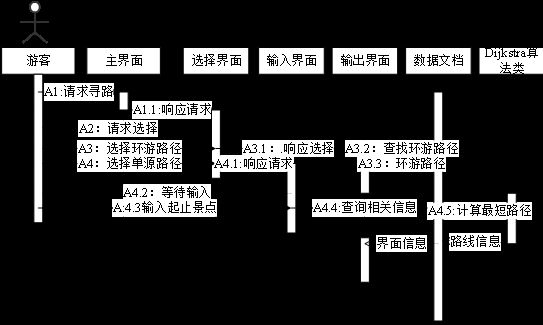
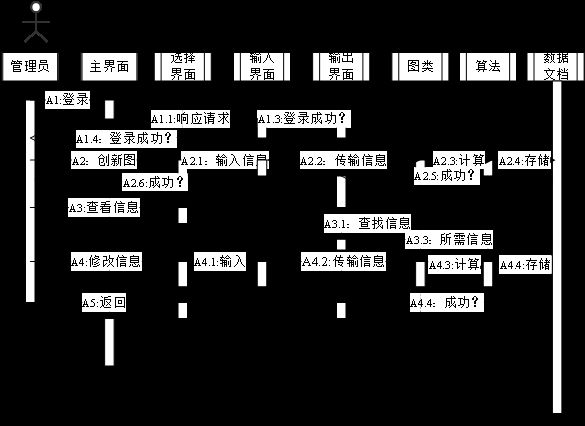
图4-2显示了管理员用户与系统发生交互时的时序情况，其实现了第三章中的用例1、用例2、用例5和用例6。 首先系统根据初始化时默认的密码确认管理员身份，然后根据管理员的需要，完成各响应。在系统通过各种界面和用户在进行交互时，整个交互界面作为后台程序控制界面的使用角色，不停地控制数据文件、其他功能类为前端提供数据和服务，并将结果和要处理的信息分别发送给用户和后台。 图4-2 管理员角色时序图

5.详细设计

5.1类抽象和定义

5.1.1实体对象

实体对象是存储信息的软件对象。实体对象是实体类的实例，其属性与其他实体类的管下载静态建模期间确定。为能在系统关闭和以后启动时将其所封装的信息保留下来，可将实体对象映射到一个文件系统或数据文件中，对于这一数据文件的设计见下文第五章。
由第二章中的问题定义可知，本次课设中要处理的现实实体是景点和道路，为在计算机中处理和表示他们间的关系，需要构建和它们相关的图模型。则系统中应包含对景点的抽象类、对道路的抽象类并将其关系抽象为导游图类。其中，系统关注景点的描述信息、出度和邻接关系，关注道路的长度及其端点，并关注图模型中各种信息的初始化、获取和处理。但进一步分析可发现，由于两景点间的道路存在与否及其长度都可由邻接矩阵中的元素表示，系统不关注道路的更多细节，因此可以省去道路类以优化设计。即可在此系统中设计景点类和图模型类，分别命名为Scene和GuidanceMap。
在实际场景中，Scene所代表的实际事物状态的改变引发GuidanceMap的改变。但由于安全性需求的存在，需要对景点中的信息做部分封装，因而需要通过Guidance类来控制、获取和处理有关Scene的信息，二者间存在由Guidance到Scene的依赖关系。因而Scene类中只需要存放景点的名称name、该景点的最大出度degree、当前已连接景点数adjacencies、和依赖于GuidanceMa的编码信息code，并通过设置、控制方法实现信息的封装和保护。此外，还需要适应各种程序场景下的构造方法，以满足不同的需求。在GduidanceMap类中，关注公园最大景点数n和当前已存在景点数current并保证其与经典出度的关系满足哈密顿环定理，用Scene数组scenes存储景点信息，实现对景点信息的封装和与景点间的依赖关系。
此外，对于GuidanceMap来说，在初始化、使用和维护的过程中，同样需要各种方法来保证其性能，这些方法不需要被外界调用，因而被封装为私有方法，只在某些特殊情况发生时，由其他方法调用，从而使得该类的性能更加稳定。为进一步简化问题，在该类中封装景点信息时，将所有景点按照其加入整个图的吮吸进行编号，由于景点姓名和景点整体都以数组形式存放，所以该编号实际上就是此两个数组的下标。只要在对各种景点捡的信息加以改变时，保证此二者间的对应关系，就可以保证该编号的正确性。在问题处理中，实际上用户只关注景点姓名和路线信息，并不关注整个景点的具体状况，封装景点类除了保证对现实实体的抽象，还提供了程序的扩展性。如果需要扩展对于景点的其他操作，可以只改变景点类的状态，而不需要更改图模型和其他处理的算法类。
在实际处理整个图的过程中，其实程序只关注某两个景点间的编号以及邻接表中这两个编号的景点上对应的权值由此可进一步简化程序的处理流程和复杂度，也节省了不必要的开支。在判断某个景点是否属于该图的时候，也不是遍历关于景点的数组，而是遍历该姓名数组。在程序中，对于数字的处理显然比对类、字符串等更简单，耗费也更少。结合实际场景，在给出路线的时候，既可以给出景点名称对应的路线， 也可以给出景点编号对应的路线。
而在维护这些数组时，如果将某个景点删去，可以直降其对应位置上的信息删去，而不处理整个空间，以减少不必要的耗费。但这样就可能存在数组空间不足，或者空间过分冗余的情况，则需要resize和deleteNull两个处理方法，在空间不足时对整个空间加以扩展或者收缩，且保证其中存放的所有值不改变。同时，由于当前各个数组的状态并不能直接反应整个图的情况，需要设置计数器来统计当前图中所有景点的个数，并通过该数字和预设的所有景点的个数进行比较获取当前图是否满或空。此外，还在图模型类中设置了各种封装后信息的获取方法，从而减少获取信息时候的耗费，并保证对所有信息的封装。对于那些不希望由外界设置值的信息，则不提供其设置方法，从而保证信息的安全性。
由此，可以得出对于该问题中景点类、导游图类两个实体类的方法，如图5-1所示。

图5-1实体类GuidanceMap、Scene类图

5.1.2算法对象

算法对象封装了在问题域中使用的算法，通常是对实体对象的操作，用来操作实体对象中封装的数据。在本系统中，分别构建Dijkstra算法和旅行商问题的分支限界算法两个算法对象，用于处理实体对象中的数据。

5.1.2.1旅行商问题算法对象

由2.2.2的分析可知，旅行商问题的解空间是一棵排列树，如果只需要旅行商问题的某个特定解，可以在搜索该排列树的过程中不断处死某些分支，以降低其时间复杂度，此时需要用到优先队列或者最小堆。由此，需要先为旅行商问题构造其最小堆，并定义堆中的元素节点。为处理问题的方便，直接将耗费定义为经过某顶点时的已经走过的路线长度。对整个图中的任意一个顶点，将其耗费定义为从该顶点出发，到所有与之相连的顶点中的最小耗费。将所有顶点的耗费相加，作为当前问题的最小耗费。由于该最小号耗费可以作为处死某些最小堆中某些节点的依据，且会随着对整个解空间的不断搜索而有所改变，由此，在构建最小堆的顶点时，需要将该顶点的最小耗费封装在节点当中（currentCost）。同时，为了方便比较，需要将当前整个图的最小耗费（lowestCost），也封装在该顶点类当中。
在实际问题当中，我们其实并不关注最后得到的最小耗费的值，反而更加关注得到该最小耗费的值所经历过的路线。而该路线信息，同样会随着对整个解空间的搜索而有所变化，当搜索到整个排列树的叶子节点或者所有节点都不满足构成最小耗费的条件，则需要返回不能构成哈密顿环这样的信息。由此需要在堆的节点中封装一个数组，记录其走过的所有路线（result）。该数组的长度最大值，即为整个图中所有的顶点数，即一旦遍历了图中的所有顶点都不能找到满足需要的路线，即返回一个找不到该路线的信息。由此，需要在该节点类中封装其当前走到的顶点（middle）和所有顶点的个数（n）。实际上，根据哈密顿环定理，由于之前已经对输入的数据加以限制，在本次问题的处理当中，不存在找不到该路线的情况。
完成该顶点的定义之后，构建一个用数组实现的最小堆，其根节点的位置在数组中下标为0的位置上。在数值上，对堆中的所有节点，设该节点的位置为i，其父节点的位置为（i-1）/2，其左子节点的位置为i2，右子节点的位置为i2+1。
可根据这样的关系定位堆中的任意一个节点，并根据构造的最小耗费，对其位置进行调整，以保证根节点的位置上始终都是整个堆中耗费最小的节点。由于已经将该堆中的根节点固定在下标为0的的位置上，则只需要记录其伪元素的下标位置，就可以定位该堆中的所有元素了。此时需要一个类似指针的变量rear来标记该位置（由于编程语言选择Java，此时的rear并不是一个真正的指针变量）。初始化的时候，将该变量的值标记为-1，用以记录当前堆中最后一个节点的下标，此后每当有新的元素被插入该堆中，rear的值都需要加1，则如果需要知道该堆中所有节点的数量，只需要将rear的值加1后返回，如果判断该堆是否为空，只需要判断rear的值是否为-1。
在完成对最小堆中节点和最小堆的构建之后，则可以构建旅行商算法类。上述需要在节点中使用的值，都需要在旅行商算法中保存一个原始父本，而在该算法类中，最重要的方法就是构建整个图的哈密顿环。在该方法中，首先遍历所有顶点，找到该顶点的最小耗费，将所有顶点的最小耗费相加的到整个图的最小耗费，然后开始遍历整个图。由4.1.1可知，此时遍历的是该图的邻接矩阵，该矩阵中，如果某个位置的值为-1，证明该处没有边，如果为正值，该值即为该出边的权值。则可将需要使用的常量-1定义为状态变量NOEDGE，且此状态变量不可更改。在遍历过程中，如果已经到了最后两个顶点，但此两个顶点不能跟最初的顶点构成回路，则此处的哈密顿环不存在。

图5-2 旅行商算法类类图

5.1.2.2Dijkstra算法对象

由2.2.3的分析可知，作为一种贪心算法，Dijkstra算法除了关注起止顶点的位置，在决定是否选择某个顶点加入解时，同样关注其最小耗费。保持此算法和旅行商问题算法的一致性，此处仍然将该耗费定义为该处顶点出边的权值。且为进一步简化问题，此处表示所有顶点时仍然采用上述的编码方法。由此在利用Dijkstra类的对应方法处理整个图的时候，只需要知道起止位置，整个图中所有顶点的个数以及其邻接表，就可以获取某两个顶点间的最短路线。一依次遍历图中所有的顶点，就可以得到关于每两个顶点的最短路线。而在实际解决问题当中，图中可能存在某两个顶点存在环路，导致算法不能终止，图2-1中即存在这样的环路，此时可通过其顶点总数进行判断。如果某两个顶点间的最短路线中经过的顶点数，已经超过了整个图中所有顶点的个数，显然这样的路线不能构成整个一条最短路线，此时可判断出在该图中存在了环路。此时，可调转起止顶底啊你的顺序，给出相反条件下的最短路线。根据实际经验可知，不存在这样的公园，使有两个景点间在寻找对方时，都在环路中绕圈子。由此，将算法得到的最短路径封装在数组中，调用对象需要时访问即可.

5.1.3 文件处理对象

在第三章的用例图中，除与人类对象交互外，本次课程设计的系统同样与数据文件产生交互关系。需要从文件中读取已经存在的图模型数据、输入新的图模型数据或者在文件中查找所需的信息，因而需要一个与文件交互的文件处理类，解决数据的I/O和存储。在文件处理类中，分别提供对指定文件的读写操作（getWords、writeWords），并记录读取到的字符串（result）及其个数（count）。在具体的用例中，系统可根据需要实例化或者析构文件处理对象，利用其中的方法获得文件中的数据或者向文件中写入数据。

5.1.4交互对象

交互对象是系统中调用各个类中的方法并实现与人类用户的交互的一类对象，在本次课程设计中，通过图形化界面类完成这一功能。由于这些类并不执行具体的功能，实际上也不存储或处理任何的信息，所以可以进一步简化其设计，仅在其类中处理各种外部事件，进而调用其他各个类的方法，而通过各个类的构建与消亡完成界面的跳转，从而实质上让这些界面充当接口的作用。这体现了面向对象中封装、多态和工厂的设计模式，从而可以进一步简化设计。由于这些交互对象没有实质性的功能，且已在第三章将其抽象为一个控制器角色，所以本次设计仅关注其在交互中实现的功能，在第5.3中具体解释其操作流程，详细界面设计源码见附录三。

5.2系统执行流程图

综上所述，可以得到如图5-1所示的系统执行流程图。用户可据需求选择使用何种功能。当使用管理功能时，需要输入预先设定的密码，正确后才能进行的管理。选择使用寻路功能的时候根据提示输入相关的信息，系统给出相应的输出。

图5-5 系统执行流程图

5.3交互流程

5.3.1开始界面及寻路界面

开始界面如图及流程如图5-3所示，在系统开始后给出的就是当下的开始界面。在这个界面当中，系统首先和用户角色发生交互。但是此时系统尚且不知道具体是哪个角色在使用系统。由此，系统需要先要判断是哪种角色使用了系统，然后跳转到相应的界面，给出相应功能处理。寻路界面如图及流程如图5-4所示，当系统先要判断是游客角色使用了系统，然后跳转到此界面，给出功能处理。要让游客决定查找的是某两个景点间的单源最短路径，还是整个公园的环游路径。

图5-6 主界面（开始界面）及寻路界面执行流程

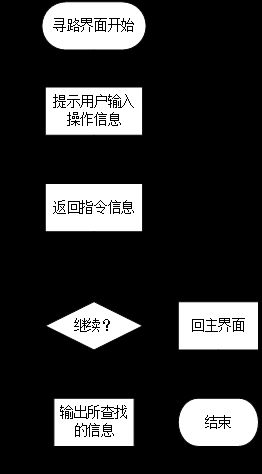
5.3.2登录界面及管理界面

当用户企图以管理员身份接入系统时，系统首先要判断其是否具有管理权限，由此，需要由管理员进行登录。其登录界面如图5-6所示。在此处，如果用户给出的密码不能和系统初始化时给出的密码对应，则不能登录系统，使用相应功能。
在用户登录进系统后，系统提示给出用户可以执行的功能，由用户进行选择。其流程图如图5-7所示。

图5-7 登录界面执行流程及管理界面执行流程

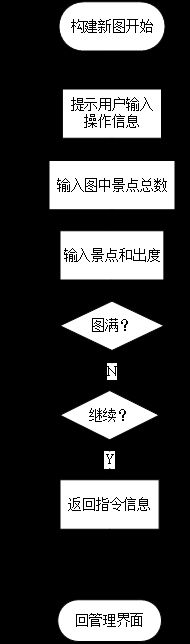
5.3.3创建新图及构造景点界面

在上一级界面中，如果用户选择了创建新图，则跳转到响应界面，并执行如图5-8所示的流程。在管理界面中，如果用户选择管理道路长度，则会跳转到如图5-10所示的界面和执行流程。如果此时数据文件中没有相应数据，则需要先提醒用户给出相应的数据。

图5-8 构建新图界面及管理道路界面的执行流程

5.4小结

本章完成了系统的的详细设计，进行了动态交互建模，通过各个界面类的设计完成了整个系统中的流程跳转、各个类的功能调用和与用户的交互，通过通信图、流程图完整地描述了第三章中的各个用例，也实现了第四章中各个类类体之间的交互。

6.调试分析

本次课程设计所创建系统是在Windows系统上运行的Java程序，系统配置应该与1.4中相同，即Windows7及以上的系统环境、JDK13及以上的Java版本。完成配置后依次调试上述各类。

6.1导游图类

首先创建一个空图以验证图类的构造方法否运行良好，随后将该图大隐刀控制台以验证toString方法是否运行良好，并可通过此方法观察其中的值，随后一次创建含有各种参数的导游图类并更改其中邻接、景点等值，依次将各个值打印在控制台上，观察其值。

6.2旅行商算法类

将图2-1中的相关数据创建为图类，构建邻接表后，创建SalesMan类，调用其中的相关方法，并将其中的数据输出，观察发现得到了与预期相符的结果，证明该类运行良好。

6.3迪杰斯特拉算法类

将图2-1中的相关数据创建为图类，构建邻接表后，创建Dijkstra类，调用其中的相关方法，并将其中的数据输出，观察发现得到了与预期相符的结果，证明该类运行良好。

6.4文件处理类

创建文件处理类CopeFile，将经典的姓名、出度、邻接表和环游路线依次存入四个文件中，将四个文件中的内容读回后用其中内容创建GuidanceMap类，可实现数据的存储与复原。

6.5界面

创建新线程开始运行第一个界面，按照使用流程分别检验正确输入和错误输入，判断程序能否给出相应的应答并并正常跳转、退出，若有错误信息，将错误信息输出在控制台上，观察控制台检测器结果。

P.S.我知道下面的这部分界面很丑，但是我又不是个学美术的是吧，就别要求那么多了。我同学75块钱买的界面跟这长得一毛一样，你说有那钱买奶茶不好吗，要真钱多的没地方花，给我啊，我不用75，45做一套界面就行。
P.P.S.请千万不要用Java写界面，哪怕eclipse集成了window builder也不要用，乖乖换QT或者H5。当然你要非要用window builde请自行百度……
要是你让我用Java写界面……给750我也……
750肯定写，谁会跟钱过不去呢。

7.使用说明

7.1角色划分

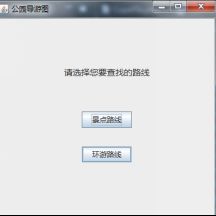
本系统的使用过程可以参照第五章的流程图和第三章的用例文档，但系统开始使用后会时时提醒用户进行相应操作并对用户的错误操作进行一定的限制。系统的开始界面如图7-1所示，在该界面上提醒用户进行相应选择是对系统中的信息加以管理还是直接查找所需的路线。

图7-1 系统开始界面

7.2游客功能

当用户选择直接查找路线时，会进入如图7-2所示的选择界面，可以继续根据提示选择，此时执行第三章用例3和用例4。

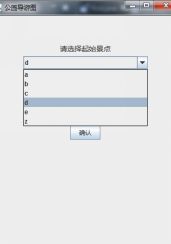
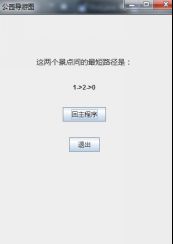
当用户选择查找环游路线时，会进入如图7-3所示界面，上面显示了最短路线中各景点的编号。

图7-2 路线选择界面 图7-3最短环游路线显示界面

当用户选择查找两景点最短路线时，会进入如图7-4所示界面，上面显示了中各景点的名称以供游客挑选。当用户做出选择后，界面继续跳转并显示这两个景点之间的最短路线。

图7-4最短路径显示界面

7.3管理功能

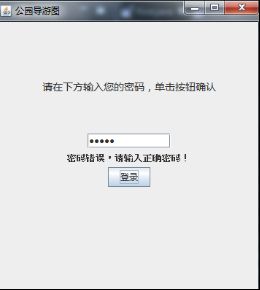
在7.1的角色划分中，当用户选择管理系统时，会进入如图7-5所示的登录界面。系统初始化时默认特定管理员和密码，直到密码输入正确才可以继续使用。可以继续根据提示选择，自此开始执行第三章中用例1、用例2、用例5和用例6。

图7-5登录界面

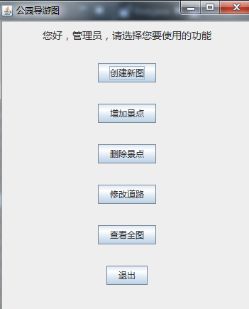
密码输入成功后进入如图7-6所示的管理功能选择，可选择相应功能。

图7-6管理功能选择界面

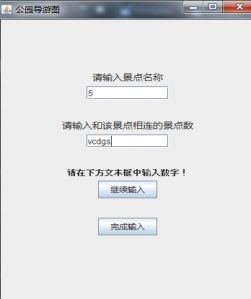
在构建系统而时候已经默认输入了一张公园导游图，所以当选择构建新图的时候，默认删除初始图，并进入如图7-7中左上所示的界面，需要输入景点的总数，如果输入非数字，系统会给予提示。当输入完成后，进入如图7-7右上的界面，依次输入景点名称和出度。如果输入满，则进入如图7-7左下的界面，确认输入。此时进入图7-7右下的界面，可以在其中查看刚刚输入的信息，如果不对，则可进入修改景点界面和修改道路界面，修改景点界面和创建景点界面相同，体现了复用的设计思想。在刚进入管理界面是使用查看全图同样进入7-7右下的界面。

图7-7创建景点界面 在管理界面或者确认界面进入道路管理时，进入如图7-8所示的界面，可以选择起止点并加以管理。 图7-8管理道路界面

8.总结

8.1数据结构

本次课程设计主要采用数据结构中的图模型及其相关算法，使用到的主要算法包括寻找单源最短路径的Dijkstra算法和旅行商问题的分支限界算法，在旅行商的分支限界算法中还使用了以最小耗费为优先级的最小堆。数据结构的封装具有良好的可扩展性，算法复用性较好。

8.2面向对象方法

本次课程设计主要采用面向对象的思想，自顶向下进行设计，对涉及到的各个对象进行了很好的封装，实现了多态和继承的特性并采用了如工厂、接口等设计模式，深化了对面向对象程序设计的理解和思考。

8.3软件生存周期

本次课程设计遵循一般软件生存周期和基于建模的分析方法，从实际情况及需求出发，通过问题分析、需求分析、概要设计和详细设计设计实现了公园导游图系统，设计过程中采用UML中的用例图、类图、通信图等将各个过程加以表示，逻辑严谨清晰，系统的可扩展性和复用性较好。

8.4问题处理

本次课程设计处理的问题涉及图模型的建立和使用、单源最短路径问题遗迹旅行商问题，涉及到Dijstr算法、回溯和分支限界算法，简单处理了相关数据在数据文件中的存储和使用。是对相关内容所涉及的数据结构、程序设计、算法分析等相关课程内容的综合利用和整合。
在具体的设计过程中，逐步建立问题模型并围绕软件生存周期设计系统，从问题分析入手，找到相关问题的解和得出该解的算法，验证该算法的正确性并尝试优化算法。随后根据问题，逐步建立需求、数据、概念和设计的相关模型，并完成功能测试。最终得到具有良好的交互性、可扩展性及复用性且安全性较好的系统。
此系统交互性较好，可根据使用权限的不同管理某公园内各景点及景点间路线长度，或查询与之有关的信息。在对系统内信息进行管理时对数据进行了较好的封装，安全性和可扩展性较高，可以实现对公园内各景点及景点间路径的存在和路径长度的创建或更新，并能根据需要给出某两个景点间的最短路径和环游整个公园的最优路线。

参考文献

[1]卢开澄,卢华明.图论及其应用[M].北京：清华大学出版社,1995.
[2]卜月华,王维凡,吕新忠.图论及其应用[M].南京：东南大学出版社,2015,5.
[3]Gomaa,H.Real-Time Software Design for Embeded Systems[M].郭文海,林金龙.北京：机械工业出版社,2019.1
[4]Kruse,R.L.Data Structures And Program Design in C++[M].北京：高等教育出版社，2001.5.
[5]杨晶浩.现代软件工程应用技术[M].北京：北京理工大学出版社,2017,5.
[6]李必信,廖力,王璐璐,孔祥龙,周颖.软件架构理论与实践[M].北京：机械工业出版社,2019,1.
[7]Gomaa,H.Real-Time Software Design for Embeded Systems[M].郭文海,林金龙.北京：机械工业出版社,2019.1
[8]王晓东.计算机算法设计与分析[M].北京：电子工业出版社
[9]Gamma,E.Helm,R.Johnson,R.Vlissides,J.Design Patterns:Elements of Reuseable Objet-Oriented Software[M]. 李英军,马晓星,蔡敏,刘建忠,吕健.北京：机械工业出版社,2019.3