LeetCode343 整数拆分
题目描述
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
题目思路
这道题的做法是采用动态规划, 状态: F(i)代表一个整数i被拆分成至少两个正整数之后,乘积的最大值。那么难点在于如何确定状态方程。通过暴力搜索—》 记忆化搜索—》动态规划的步骤来慢慢深入。
暴力搜索
对于给定一个正整数,穷举所有分解的情况,如下图所示。
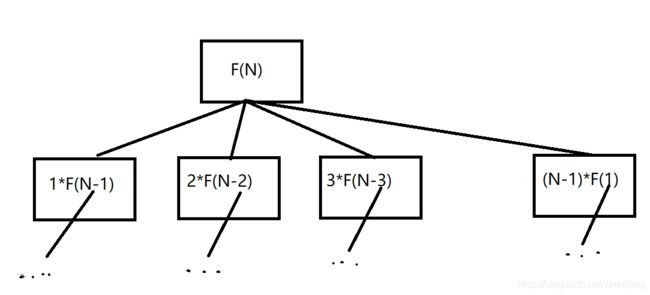
可以得到一个递归表达式:
F(n) = max(i*F(n-i)), i = 1,2, ..., n - 1
当然,如果i*(n - i)的值比i*F(n-i)大,那么就不需要继续分解了。
暴力穷举所有分解的情况取最大值,代码如下:
class Solution {
public int integerBreak(int n) {
if(n == 2){
return 1;
}
int res = 0;
for(int i = 1; i <= n; i ++){
res = Math.max(res,Math.max(i * (n - i), i * integerBreak(n - i)));
}
return res;
}
}
记忆化搜索
上面暴力搜索的算法超时是无疑的,因为有很多的重复计算,所以我们要将已经计算好的值保存下来,下次碰到就直接拿来用就可以了。具体操作是用一个数组将计算好的值存下来以备后用。
class Solution {
int[] memory;
public int integerBreak(int n) {
memory = new int[n + 1];
return integerBreakHelper(n);
}
public int integerBreakHelper(int n) {
if(n == 2){
return 1;
}
if(memory[n] != 0 ){
return memory[n];
}
int res = 0;
for(int i = 1; i < n; i ++){
res = Math.max(res,Math.max(i * (n - i), i * integerBreakHelper(n - i)));
}
memory[n] = res;
return res;
}
}
动态规划
上面方法是递归,自顶向下。而动态规划是自底向上。
memory数组是存放分解后最大乘积。
class Solution {
public int integerBreak(int n) {
int[] memory = new int[n + 1];
memory[2] = 1;
for(int i = 3; i <= n; i ++){
for(int j = 1;j < i;j ++){
memory[i] = Math.max(memory[i],Math.max(j * (i - j), j * memory[i - j]));
}
}
return memory[n];
}
}
动态方程就是:
memory[i] = Math.max(memory[i],Math.max(j * (i - j), j * memory[i - j]));
或者写做:
F[i] = Math.max(F[i],Math.max(j * (i - j), j * F[i - j]));