2020牛客多校联赛第二场 （BCDF）

B：Boundary

题目

题目描述
Given n points in 2D plane. Considering all circles that the origin point (0,0) is on their boundries, find the one with the maximum given points on its boundry. Print the maximum number of points.

输入描述:
The first line contains one integer n (1≤n≤2000), denoting the number of given points.
Following n lines each contains two integers denoting a given point (x,y).
It’s guaranteed that the points are pairwise different and no given point is the origin point.

输出描述:
Only one line containing one integer, denoting the answer.

翻译

题目描述
给定二维平面上的n个点。考虑原点(0,0)在其边界上的所有圆，找出其边界上给定点最大的圆。打印最大点数。

输入描述:
第一行包含一个整数n(1≤n≤2000)，表示给定点的个数。
在n行之后，每一行都包含两个整数，表示一个给定的点(x,y)。
它保证这些点是两两不同的并且没有给定的点是原点。

输出描述:
只有一行包含一个整数，表示答案。

例子

输入
4
1 1
0 2
2 0
2 2
输出
3

大意

找出所给点的所在圆中最大的数。（大概是这个意思）
考虑圈 （x-1）^ 2 +（y-1）^ 2 = 2，我们可以看到原点在其边界上，并且有3个给定点 {（0,2），（2,0），（2,2）}，（0 ，2 ），（2 ，0 ），（2 ，2 ） 在它的边界上。

思路

列算式，枚举

代码

以下是在牛客网上看得

#include
#define ll long long
using namespace std;
const int maxn=2e6+10;
struct Point
{
    double x,y;
}p[maxn];
map<pair<double,double>,int>mp;
int ans=0;
void solve(Point a,Point b,Point c)
{
    double f1,f2,f3,f4,f5,f6,f7,f8;
    f1=a.x*a.x-b.x*b.x+a.y*a.y-b.y*b.y;
    f2=a.y-c.y;
    f3=a.x*a.x-c.x*c.x+a.y*a.y-c.y*c.y;
    f4=a.y-b.y;
    f5=2.0*(a.y-c.y)*(a.x-b.x)-2*(a.y-b.y)*(a.x-c.x);
    f6=a.x-c.x;
    f7=a.x-b.x;
    f8=2.0*(a.y-b.y)*(a.x-c.x)-2*(a.y-c.y)*(a.x-b.x);
    double x=(f1*f2-f3*f4)/f5;
    double y=(f1*f6-f3*f7)/f8;
    mp[{x,y}]++;
    ans=max(ans,mp[{x,y}]);
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>p[i].x>>p[i].y;
    for(int i=0;i<n;i++)
    {
        mp.clear();
        for(int j=i+1;j<n;j++)
        {
            if(p[i].x*p[j].y==p[i].y*p[j].x) //防止三点共线
                continue;
            solve({0.0,0.0},p[i],p[j]);
        }
    }
    cout<<ans+1<<endl;
    return 0;
}

C：Cover the Tree

题目

题目描述
Given an unrooted tree, you should choose the minimum number of chains that all edges in the tree are covered by at least one chain. Print the minimum number and one solution. If there are multiple solutions, print any of them.

输入描述:
The first line contains one integer denoting the size of the tree.
Following n−1 lines each contains two integers u,v (1≤u It’s guaranteed that the given graph forms a tree.

输出描述:
The first line contains one integer k, denoting the minimum number of chains to cover all edges.
Following k lines each contains two integers u,v (1≤u,v≤n), denoting a chain you have chosen. Here u=v is permitted, which covers no edge.

翻译

题目描述
对于一个没有根的树，应该选择最小的链数，使树的所有边都被至少一条链所覆盖。打印最小的数字和一个解决方案。如果有多个解决方案，打印其中任何一个。

输入描述:
第一行包含一个整数，表示树的大小。
每一行n−1包含两个整数u,v(1≤u 它保证给定的图形成一个树。

输出描述:
第一行包含一个整数k，表示覆盖所有边的链的最小数目。
每个k行包含两个整数u,v(1≤u,v≤n)，表示你选择的链。这里允许u=v，它不包含任何边。

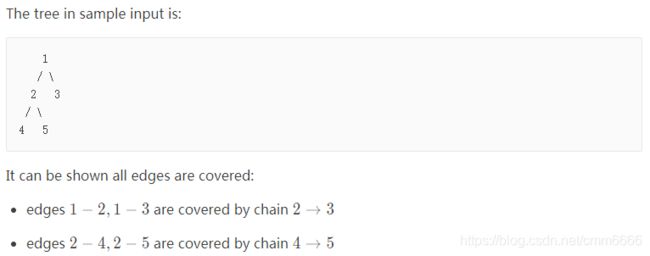
例子

输入
5
1 2
1 3
2 4
2 5
输出
2
2 3
4 5

大意

思路

注意一下叶节点的存储和遍历。

代码

#include
using namespace std;
int a[201010],n,u,v,tmp,tree[201010];
int main()
{
    std::ios::sync_with_stdio(false);//加快输入
    cin.tie(0);//取消cin与cout之间的锁定，加快执行效率
    
    cin>>n;
    for(int i=1; i<n; i++)
    {
        cin >> u >> v;
        a[u]++;
        a[v]++;
    }
    
    for(int i=1; i<=n; i++)
    {
        if(a[i]==1)//筛选出边缘数字
        {
            tmp++;//记录个数
            tree[tmp]=i;//记录数字本字
        }
    }
    
    cout << ((tmp+1)/2) <<endl;//输出链数
    for(int i=1; i<=((tmp+1)/2); i++)
    {
         cout << tree[i] << " " << tree[i+(tmp/2)] <<endl;
    }
}

D：Duration

题目

题目描述
Given two moments on the same day in the form of HH:MM:SS, print the number of seconds between the two moments.

输入描述:
Input two lines each contains a string in the form of HH:MM:SS (00≤HH≤23,00≤MM,SS≤59), denoting a given moment.

输出描述:
Only one line containing one integer, denoting the answer.

翻译

题目描述
在同一天以HH:MM:SS的形式给出两个时刻，打印这两个时刻之间的秒数。

输入描述:
输入两行HH:MM:SS(00≤HH≤23,00≤MM,SS≤59)字符串，表示给定时刻。

输出描述:
只有一行包含一个整数，表示答案。

例子

示例1
输入
12:00:00
17:00:00
输出
18000

示例2
输入
23:59:59
00:00:00
输出
86399

大意

输入两个时间，输出两个时间之差。

思路

C#：DateTime类
C++：小时、分与秒之间的转换。
注意差值为负数时，取绝对值。

代码

C#

class Program
    {
        static void Main(string[] args)
        {        
            string str = Console.ReadLine();
            string st = Console.ReadLine();
            DateTime date1 = DateTime.Parse(str);
            DateTime date2 = DateTime.Parse(st);
            TimeSpan ts = date2 - date1;
            if(ts.TotalSeconds<0)
            {
                ts = date1 - date2;
            }
            Console.WriteLine(ts.TotalSeconds);
 
            Console.ReadLine();
        }
    }

C++

int main()
{
    int s,f,m;
    int k1,k2;
    scanf("%d:%d:%d",&s,&f,&m);
    k1 = s*3600+f*60+m;
    scanf("%d:%d:%d",&s,&f,&m);
    k2 = s*3600+f*60+m;
    printf("%d",abs(k1-k2));
    return 0;
}

F：Exclusive OR

题目

题目描述
Given n integers A1​,A2​,⋯,An​. For all i in {1,2,⋯,n}, you should determine the maximum value you can get if you repeatably choose exactly i integers a1​,a2​,⋯ai​ and calulate their XOR sum a1​⊕a2​⊕⋯⊕ai​.
Please notice that you can choose one integer multiple times for one i in this problem.

输入描述:
The first line contains one integer denoting the number of given integers.
The second line contains n integers ：

输出描述:
One line containing n integers, where i-th integer denotes the maximum value you can get if you repeatably choose i integers and calulate their XOR sum.

翻译

题目描述
已知n个整数A1 A2，⋯⋯An。对于{1,2，⋯⋯n}中的所有i，你应该确定你可以得到的最大值，如果你重复地选择i整数a1,a2，⋯⋯ai，并计算它们的XOR和a1⊕a2⊕⋯⋯⊕ai。
请注意，在这个问题中，你可以为一个i多次选择一个整数。

输入描述:
第一行包含一个整数，表示给定整数的数量。
第二行包含n个整数:

输出描述:
一行包含n个整数，其中第i个整数表示如果重复选择i个整数并计算它们的异或和可以得到的最大值。

例子

输入
4
1 4 5 7
输出
7 6 7 7

大意

矩阵，求最大值

思路

经推后，发现最大值就在正方形的右下角，所以就在这三个值当中的任一个。因为是坐标的公倍数，数字越大，公倍数就越大。

代码

以下是在牛客网上看得

#include
using namespace std;
typedef long long ll;
const int maxn=5009;
int n,m,k,a[maxn][maxn];
int main(){
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
        if(k==1) a[i][j]=i*j/__gcd(i,j);
        else a[i][j]=max(i*j/__gcd(i,j),max(a[i-1][j],a[i][j-1]));
    ll ans=0;
    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) ans+=a[i][j];
    cout<<ans;
}