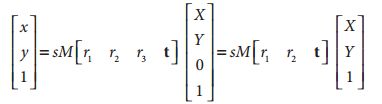03月11日单应矩阵与鸟瞰图IPM变换
修订:# 4 如何求解原图像中像素点的实际距离;20200522
文章目录
- 0.0 相关知识:
- P:相机透视视角下 a帧和b帧之间旋转矩阵通过特征点对齐, 获得的r和t; 如果a帧和b帧变成鸟瞰图,特征点对齐的r和t还是同一组吗?
- Simplify P:2D-2D;且特征点都位于一个平面上,获得的r和t(即单应矩阵)
- 1 储备知识点
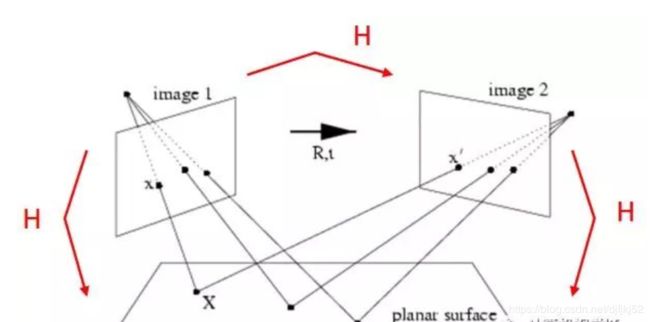
- 1.1 单应矩阵等同于旋转+平移
- 1.2 归一化
- 1.2.1尺度不确定性
- 1.2.2初始化的纯旋转问题
- 1.2.3多于8对点的情况
- 2 鸟瞰图——逆透视IMP(属于透视变换的一种)
- 2.0 求解IPM的方法包括
- 1.简单的对应点单应变换方法
- 2.简化相机模型的逆透视变换
- 3.其他IPM变换方法:
- 2.1 实例:“对应点”单应变换的IPM
- 2.2 实例:基于消失点,基于相机姿态的IPM
- 3.0 关于尺度的问题,相关论文:
- 3.1 Vision-based ACC with a Single Camera: Bounds on Range and Range Rate Accuracy——著名的Mobileye论文
- 3.2 Robust Vehicle Detection and Distance Estimation Under Challenging Lighting Conditions——IPM的鸟瞰图展示距离
- 4.0 综上所述
- 4 如何求解原图像中像素点的实际距离;
0.0 相关知识:
特征匹配分为:
(1)2D-2D ;
(2)2D-3D ;
(3)3D-3D。
P:相机透视视角下 a帧和b帧之间旋转矩阵通过特征点对齐, 获得的r和t; 如果a帧和b帧变成鸟瞰图,特征点对齐的r和t还是同一组吗?
Simplify P:2D-2D;且特征点都位于一个平面上,获得的r和t(即单应矩阵)
1 储备知识点
1.1 单应矩阵等同于旋转+平移
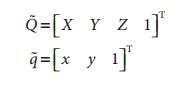
![]()
这里引入参数s,它是任意尺度的比例(目的是使得单应性定义到该尺度比例)。通常根据习惯放在H的外面。
1.2 归一化
单应性矩阵取决于一个尺度,那么通常归一化,以使得h33=1
2D-2D相机位姿估计存在以下三个敏感的问题:
- https://zhuanlan.zhihu.com/p/92221963
- 链接:https://www.jianshu.com/p/fbf56587a268
1.2.1尺度不确定性
用上面的方法估计出的相机平移向量t的值并没有单位,也就是说相机移动的距离只有相对值,没有绝对值。这是单目相机固有的尺度不确定性问题,无法从根本上解决。因此单目SLAM中一般把初始化后的t归一化,即把初始化时移动的距离默认为1,此后的距离都以这个1为单位。
1.2.2初始化的纯旋转问题
单目初始化不能只有旋转,必须要有一定程度的平移,否则由于t趋近于0,导致无从求解R或者误差非常大。
1.2.3多于8对点的情况
如果匹配的点对数多于8(大多数情况都是这样),可以考虑充分利用这些点,而不是只从中选择8对用于计算。推荐的算法是随机采样一致性(Random Sample Consensus,RANSAC),该算法可以有效地避免错误数据对整体结果的影响。在代码中,只需要将findFundamentalMat函数的第三个参数从CV_FM_8POINT换成CV_FM_RANSAC就可以了。
2 鸟瞰图——逆透视IMP(属于透视变换的一种)
透视变换的作用是让我们从另外一个角度观察图片中的场景,例如俯视。它能帮助我们避免例如“近大远小”造成的图像世界与现实世界的偏差,其方法的本质是“映射”,将原图像的像素点按照一定的“比例”映射到另外一张图上。
IPM变换具有很多应用,求取IPM图像的方法亦是有很多
2.0 求解IPM的方法包括
https://blog.csdn.net/feiyang_luo/article/details/103555036
1.简单的对应点单应变换方法
-
输入:至少四个对应点对,不能有三点及以上共线,不需要知道摄相机参数或者平面位置的任何信息。
-
数学原理:利用点对,求解透视变换矩阵,其中map_matrix是一个3×3矩阵,所以可以构建一个线性方程组进行求解。如果大于4个点,可采用ransac的方法进行求解,一边具有更好的稳定性。
-
选点方法:一般采取手动选取,或者利用消影点(图像上平行线的交点,也叫消失点,vanish point)选取。
2.简化相机模型的逆透视变换
利用相机成像过程当中各种坐标系之间的转换关系,对其基本原理进行抽象和简化,从而得到世界坐标系和图像坐标系之间坐标的对应关系,并对逆透视变换的坐标关系进行公式化描述。这种逆透视变换形式简单,计算速度快,并且适用于复杂道路场景。
- Stereo inverse perspective mapping,考虑了上下俯仰角和水平偏航角度的矫正,但是存在水平线弯曲误差。
- 基于消失点的俯仰角和偏航角计算
- 基于消失点,基于相机位姿,在相邻帧中加入了俯仰角的修正
3.其他IPM变换方法:
相比较于以上几种方法来说,更多的是应用了多视图几何的知识来得到IPM变换。
- 已知相机位姿,利用求单应矩阵得到IPM:在已知相机pose情况下,可将相机向路面方向旋转90度-俯仰角,那么得到一个新的相机pose,此时的相机是垂直与路面向下,那么得到的图像自然也就是IPM图像。
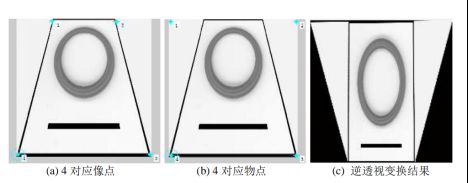
2.1 实例:“对应点”单应变换的IPM
https://www.cnblogs.com/tiandsp/archive/2012/12/16/2820916.html
2.2 实例:基于消失点,基于相机姿态的IPM
参考:《Real time Detection of Lane Markers in Urban Streets》
- https://blog.csdn.net/yeyang911/article/details/51915348
- https://blog.csdn.net/yeyang911/article/details/51912322
- https://blog.csdn.net/weixin_44409075/article/details/97892652
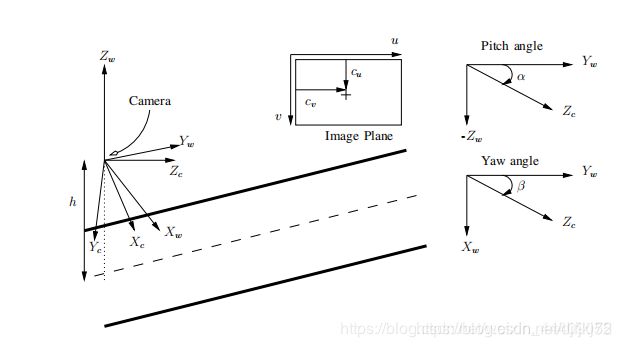
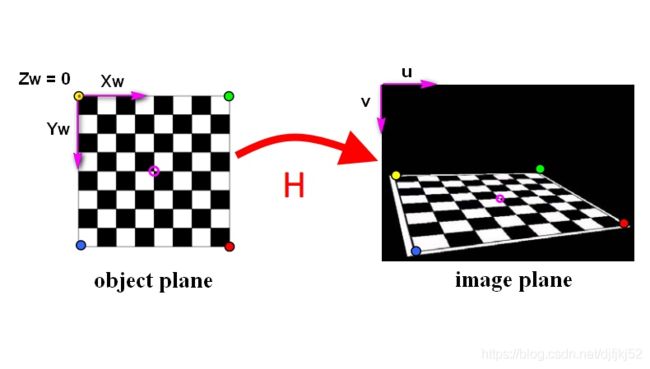
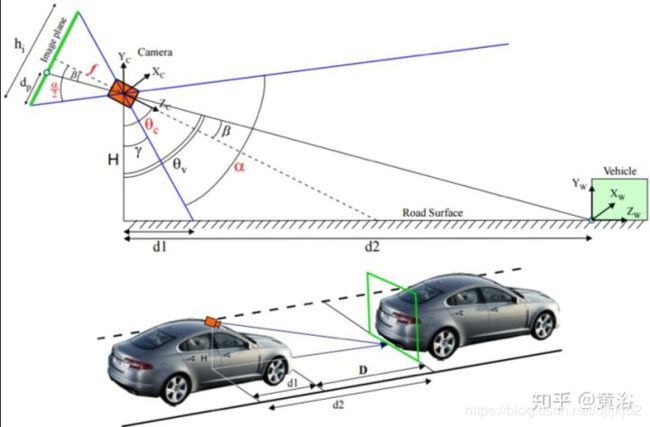
为了获得输入图像的IPM,我们使用相机内参(焦距和光学中心)和外部(俯仰角,偏航角和地面高度)参数来执行此转换。如图所示, 我们首先定义一个世界坐标系{Fw} = {Xw,Yw,Zw}(以相机光学中心为中心),相机坐标系{Fc} ={Xc,Yc,Zc},以及图像坐标系{Fi} = {u,v}。 我们假设相机框坐标系的Xc轴停留在世界坐标系XwYw平面中,且相机只存在俯仰角α(上下)和偏转角β(左右)但没有滚动。 相机坐标系中心在地平面上方的高度为h。


3.0 关于尺度的问题,相关论文:
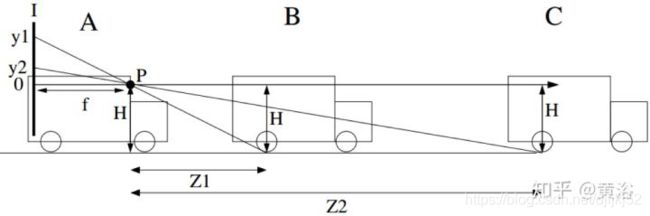
3.1 Vision-based ACC with a Single Camera: Bounds on Range and Range Rate Accuracy——著名的Mobileye论文
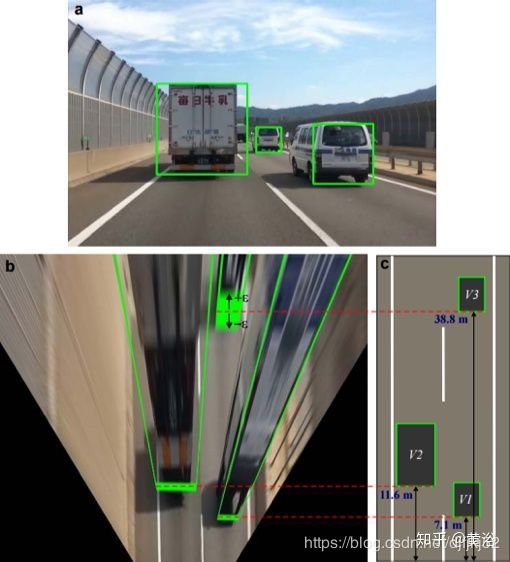
3.2 Robust Vehicle Detection and Distance Estimation Under Challenging Lighting Conditions——IPM的鸟瞰图展示距离
4.0 综上所述
(1)直接计算两帧a,b得到的单应矩阵,包含了旋转与平移(R,T),但是T是一个没有单位的量,经过了归一化。
(2)尺度问题来源于单目中路标点的深度具有不确定性(所以才反投影到归一化平面上),也就是说尺度缩放实际作用的是两个相机之间的平移缩放。
(3)鸟瞰图,等同于顶视图,纯2D的图像。 2D对应的平面位置回到3D是准确的,但在2D图像上肯定是被压缩了。
(4)如果限定了相机的高度H,尺度虽然没有限定,但是可以用来还原部分3D信息。如果包含了相机的完整姿态,可以用来进行测距。
(5)对于特征点,鸟瞰图中求解R,T,是准确的,但尺度不确定,若已知相机姿态(包括高度),可以获得尺度确定的R,T值。
(6)对于特征点,直接通过相机的两帧数据进行透视变换,求解R,T,尺度是不确定,进行了归一化。
(7)对于特征点,两帧2D-2D数据进行透视变换求解R,T 与鸟瞰图求解R,T。本质上是相同的。都是尺度不确定的,经过了归一化处理的。
(8)如果希望得到求解相机自身的完整姿态,需要使用2D-3D的方法,即PnP。
PnP的方法可参考https://blog.csdn.net/cocoaqin/article/details/77841261。需要输入:(1)objectPoints特征点世界坐标 (2) imagePoints特征点在摄像头下的像素点坐标 (3) cameraMatrixdistCoeffs内参矩阵和畸变矩阵。输出:(1)求世界坐标中的点在相机坐标系下的坐标 (2)求相机在世界坐标中的坐标,旋转角度。
(9)鸟瞰图中的R,T反应的是世界坐标系中的情况;两帧之间的R,T是两帧之间的,但是如果已知世界坐标系到图片坐标系的转换矩阵,依然可以求解世界坐标系中的R,T情况。
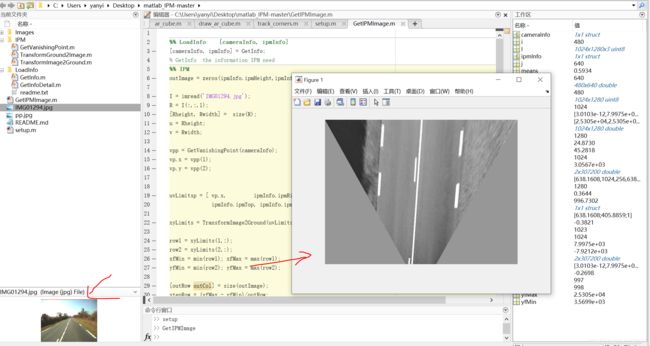
4 如何求解原图像中像素点的实际距离;
1.IPM包含3个函数。
image2ground:将图像中的像素点(u, v)对应到地平面上(Z=1)IPM的像素点(x, y);
ground2image:将IPM中的像素点(x, y)基于IPM的最大范围转换为xygrid,从而转化为uvgrid;
src2ipm:基于uvgrid插值得到IPM中像素点(x, y)的的灰度值并显示,同时转换得到IPM中每个像素点的实际距离coord;
2.如何求解原图像中像素点的实际距离;
image2ground: uvp ——> xyp;
xyp2ipmp: xyp ——> ipmp;
xmin + x.ipmp * stepcol = x.xyp;
ymax - y.ipmp * steprow = y.xyp;
从而推导出,
x.ipmp = ( x.xyp - xmin ) / stepcol;
y.ipmp = ( ymax - y.xyp ) / steprow;
3.注意:
3.1.查看x.ipmp和y.ipm的结果是否越界,需要添加越界判断;
3.2.编码的时候需要非常注意各个参数的数据类型及格式是否匹配或者一致;