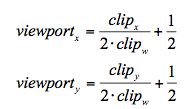Unity Shader入门精要笔记（五）：其他数学相关介绍

本系列文章由Aimar_Johnny编写，欢迎转载，转载请标明出处，谢谢。

http://blog.csdn.net/lzhq1982/article/details/73747162

前两篇介绍了Unity Shader的主要数学部分，书上还有些相关的数学介绍，将在这篇做最后的总结。

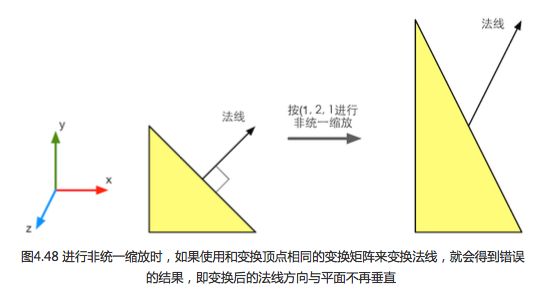
1、法线变换

法线（normal），也被称为法矢量。游戏中，模型的顶点携带的信息中，法线就是其中一种。我们变换一个模型，不仅需要变换它的顶点，还需要变换顶点法线，以便在后续处理中计算光照等。

从上一篇我们知道，点和大部分方向矢量都可以用同一个变换矩阵在两个空间之间变换。但法线用同一个变换矩阵，可能无法确保维持法线的垂直性。下面介绍一下原因。

先来了解一下另一种方向矢量：切线（tangent），也叫切矢量。也是顶点携带的一种信息。它与法线方向垂直。切线是两个点之间的差值计算得来的，因此可以直接用变换顶点的变换矩阵来变换切线。假设，这个变换顶点也就是变换切线的矩阵是3x3的变换矩阵 （因为是方向矢量，不受平移影响，不用4x4），得到空间变换公式如下：

T表示切线，上面表示切线从空间A到空间B的转换。但如果直接用同一矩阵变换法线，得到的新法线可能就不会与表面垂直了，例如：

那么怎么求法线变换的矩阵呢。答案是用法线和切线垂直的约束公式：。假设我们用矩阵G来变换法线，则有。然后结合，我们得到下面公式：

然后推导可得：

有很多人对第一个等式有疑问，请大家注意第一个等式左边是向量点乘，有个点，等式右边把向量变成了列矩阵，变成了矩阵相乘，中间没点了。其他应该没问题。看最后的等式部分，因为，把T变成列矩阵，所以，所以如果，那么上面的等式就成立了。那我们的结论就是：

如果是正交矩阵，那其逆就是其转置，那么G = ，也就是说我们可以用变换顶点的矩阵变换法线。从上一篇的表格中可以看出，旋转变换是正交矩阵，可以直接用，如果只包含旋转和统一缩放，不包含非统一缩放，则

其他情况，我们就要求的逆转置了。

2、Unity Shader 内置变量（数学）

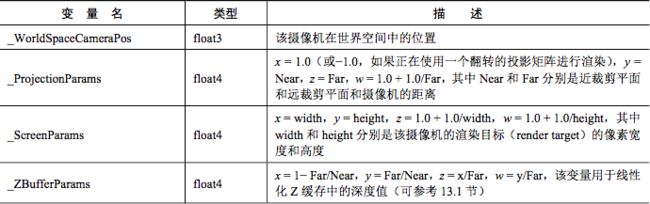
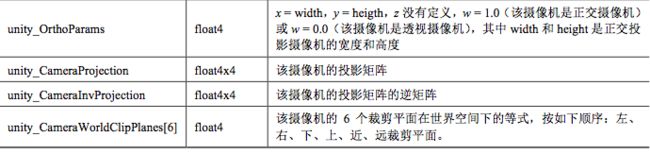
Unity给我们提供了很多有关变换的内置参数，这些内置变量可以在UnityShaderVariables.cginc文件中找到定义和说明。

1）变换矩阵

注意最后两个，Unity5.5版本中_Object2World已经变成unity_ObjectToWorld，_World2Object也变成了unity_WorldToObject，但由于Unity的向下兼容性，Unity会自动改写它们，不会出错。还有在顶点着色器中，我们往往第一行就会用到UNITY_MATRIX_MVP：mul(UNITY_MATRIX_MVP, v.vertex); 这是把顶点从模型空间转换到裁剪空间，不用我们手动变换空间了，不过这在unity5.6中已经改为：UnityObjectToClipPos(v.vertex); 在UnityShaderUtilities.cginc里，注意5.6以上版本才有这个文件。官方实现如下：

// Tranforms position from object to homogenous space
inline float4 UnityObjectToClipPos(in float3 pos)
{
    // More efficient than computing M*VP matrix product
    return mul(UNITY_MATRIX_VP, mul(unity_ObjectToWorld, float4(pos, 1.0)));
}

可以看出也是先转到世界空间，再乘以观察和投影矩阵，只不过注释那里很清楚，更高效一些。

2）摄像机和屏幕参数

读者也没有必要记住他们，以后用到了方便查阅就行。用多了就记住了。

3、Cg中矢量和矩阵类型

我在Unity Shader基础里说过Cg，是我们目前主要的着色器编程语言。这里主要说一下Cg中矢量和矩阵的表达方式。Cg中，矩阵是由float3x3、float4x4等关键字定义的，矢量是由float3、float4等关键字定义的，当然，也可以当成是1xn行矩阵或nx1的列矩阵，这取决于运算种类和运算中的位置。如下：

float4 a = float4(1.0, 2.0, 3.0, 4.0);

float4 b = float4(1.0, 2.0, 3.0, 4.0);

点积：float result = dot(a, b);

但在矩阵乘法时，参数位置决定是按行矩阵还是列矩阵进行乘法。Cg中矩阵乘法的函数是mul。

float4 v = float4(1.0, 2.0, 3.0, 4.0);
float4x4 M = float4x4(1.0, 0.0, 0.0, 0.0,
				0.0, 2.0, 0.0, 0.0,
				0.0, 0.0, 3.0, 0.0,
				0.0, 0.0, 0.0, 4.0);
//v当成列矩阵和矩阵M右乘
float4 column_mul = mul(M, v);

//v当成行矩阵左乘
float4 row_mul = mul(v, M);

//注意：column_mul 不等于 row_mul，而是：
//mul(M, v) = mul(v, tranpose(M));
//mul(v, M) = mul(tranpose(M), v);

从上面可以看出，向量、矩阵的位置会影响结果值。通常在变换顶点时，我们用右乘列矩阵的方式。有时也用左乘，省去矩阵转置的操作。

4、Unity屏幕坐标：ComputeScreenPos/VPOS/WPOS
这块内容是有点超前的，只不过涉及数学计算部分，所以放在这里，请大家记住有这么回事，后面屏幕抓取那里我们会用到ComputeGrabScreenPos，到时候还需要你回来看。好了，进入主题。

在写shader时，我们有时希望获得片元在屏幕上的像素位置。在顶点/片元着色器中，有两种方式获得片元的屏幕坐标。

1）在片元着色器的输入中声明VPOS或WPOS语义（语义以后再讲）。

VPOS是HLSL中对屏幕坐标的语义，WPOS是Cg中对屏幕坐标的语义。两者在Unity Shader中是等价的。我们可以在HLSL/Cg中通过语义的方式定义顶点/片元着色器的默认输入，不用自己定义输入输出的数据结构。如是我们可以在片元着色器中这样写：

fixed4 frag(float4 sp : VPOS) : SV_Target {
    //用屏幕坐标除以屏幕分辨率_ScreenParams.xy，得到视口空间中的坐标
    return fixed4(sp.xy/_ScreenParams.xy, 0.0, 1.0);
}

这里是把屏幕坐标转化成颜色值输出了，这是典型的用颜色值验证结果的方法，因为shader没法调试，那用颜色值输出可以直观的验证我们的结论。VPOS/WPOS是一个float4的变量，xy代表了屏幕空间的像素坐标。如果屏幕分辨率是400*300，x的范围是[0.5, 400.5]，y的范围是[0.5, 300.5]，这里的像素坐标不是整数值，因为OpenGL和DirectX 10以后的版本认为像素中心对应的是0.5。所以sp.xy/_ScreenParams.xy的结果就是(0, 0)到(1, 1)，所以左下角是黑色，右上角是黄色，结果如图：

我们用了VPOS/WPOS的xy，那zw呢，在Unity中，它们的z分量范围是[0, 1]，摄像机近裁剪面z为0，远裁剪面z为1。w分量取决于投影类型，透视投影w范围是[1/Near, 1/Far]，Near和Far对应了Camera组件中设置的近裁剪平面和远裁剪平面距离摄像机的远近。正交投影w值恒为1。

2）通过Unity提供的ComputeScreenPos函数

这个函数在UnityCG.cginc里被定义。直接上代码：

struct vertOut {
	float4 pos : SV_POSITION;
	float4 srcPos : TEXCOORD0;
}

vertOut vert (appdata_base v) {
	vertOut o;
	o.pos = mul (UNITY_MATRIX_MVP, v.vertex);
	//第一步：把ComputeScreenPos的结果保存在srcPos中
	o.srcPos = ComputeScreenPos(o.pos);
	return o;
}

fixed4 frag (vertOut i) : SV_Target {
	//第二步：用srcPos.xy除以srcPos.w得到视口空间中的坐标
	float2 wcoord = i.srcPos.xy / i.srcPos.w;
	return fixed4(wcoord, 0.0, 1.0);
}

上面代码的实现效果和第一种效果一致。从上面代码可以看出，我们用了两步获得视口空间的坐标，第一步在顶点着色器中用ComputeScreenPos函数计算的结果存在输出结构体中，第二步在片元着色器中对传过来的值进行了齐次除法得到视口空间的坐标。下面我们分析一下：

上一篇我们看到了如何将裁剪空间中的点映射到屏幕空间中。这里回忆一下，经过齐次除法后，我们把裁剪空间变换到了NDC中，不记得NDC的回头看看，NDC的xy坐标是[-1, 1]，而屏幕空间是[0, 1]，所以只要经过(x + 1) / 2的操作就可以映射过去了，所以我们得到如下公式：

这里的clip的xy都是裁剪空间的，所以除以w变成NDC下，我们再看一下ComputeScreenPos的实现（unity5.6版本）：

inline float4 ComputeNonStereoScreenPos(float4 pos) {
    float4 o = pos * 0.5f;
    o.xy = float2(o.x, o.y*_ProjectionParams.x) + o.w;
    o.zw = pos.zw;
    return o;
}

inline float4 ComputeScreenPos(float4 pos) {
    float4 o = ComputeNonStereoScreenPos(pos);
#if defined(UNITY_SINGLE_PASS_STEREO)
    o.xy = TransformStereoScreenSpaceTex(o.xy, pos.w);
#endif
    return o;
}

ComputeScreenPos输入的参数pos是经过MVP变换后的在裁剪空间的顶点坐标。UNITY_SINGLE_PASS_STEREO我们先不考虑，貌似是给vr用的。所以核心部分在ComputeNonStereoScreenPos这里，_ProjectionParams.x默认情况是1（如果使用了一个翻转的投影矩阵的话是-1，很少见）。那这段代码输出值o的各个分量是：
o.x = pos.x / 2 + pos.w / 2;

o.y = pos.y / 2 + pos.w / 2;

o.z = pos.z;

o.w = pos.w;

读者可以看出，o.x和o.y并不是视口空间的坐标，除以pos.w就和上面等式相同了，所以我们看片元着色器中的第二步就是这个操作。但为什么不在顶点着色器里的ComputeScreenPos里直接除却要在片元着色器中除呢，这是因为如果在顶点着色器中除的话，会破坏插值结果。从顶点着色器到片元着色器会有个插值的过程，这点在渲染流水线中说过了。如果我们对x/w，y/w进行插值，结果会不准确。因为投影空间不是线性空间，插值往往是线性的，所以不要在投影空间进行插值。最后我们看输出的zw没变化，还是裁剪空间的zw，所以如果使用透视投影，z范围是[-Near, Far]，w范围是[Near, Far]（读者忘了可以看上一篇的裁剪空间图）。如果是正交投影，z是[-1, 1]，w是1。

最后比书上多说一点是ComputeGrabScreenPos，后面抓取屏幕中会遇到，再过来看看。我们直接看看代码：

inline float4 ComputeGrabScreenPos (float4 pos) {
    #if UNITY_UV_STARTS_AT_TOP
    float scale = -1.0;
    #else
    float scale = 1.0;
    #endif
    float4 o = pos * 0.5f;
    o.xy = float2(o.x, o.y*scale) + o.w;
#ifdef UNITY_SINGLE_PASS_STEREO
    o.xy = TransformStereoScreenSpaceTex(o.xy, pos.w);
#endif
    o.zw = pos.zw;
    return o;
}

你会发现除了UNITY_UV_STARTS_AT_TOP这个宏判断，基本没啥变化，这个宏后面会常遇到，OpenGL是左下角为原点，DirectX是左上角为原点，所以如果是左上角为原点，那y要取反，就这点区别。

数学部分的介绍到此结束，但Shader离不开数学运算，书里推荐了扩展阅读，有兴趣的就多多研究吧。

（最后感叹一下女神这个章节的书写，我用三篇分开整理，内容还这么庞大，编辑公式好麻烦啊！！！）