GDUT 19年春季训练赛
D. Peter and Snow Blower
time limit per test:2 seconds
memory limit per test:256 megabytes
inputstandard input
outputstandard output
Peter got a new snow blower as a New Year present. Of course, Peter decided to try it immediately. After reading the instructions he realized that it does not work like regular snow blowing machines. In order to make it work, you need to tie it to some point that it does not cover, and then switch it on. As a result it will go along a circle around this point and will remove all the snow from its path.
Formally, we assume that Peter’s machine is a polygon on a plane. Then, after the machine is switched on, it will make a circle around the point to which Peter tied it (this point lies strictly outside the polygon). That is, each of the points lying within or on the border of the polygon will move along the circular trajectory, with the center of the circle at the point to which Peter tied his machine.
Peter decided to tie his car to point P and now he is wondering what is the area of the region that will be cleared from snow. Help him.
Input
The first line of the input contains three integers — the number of vertices of the polygon n (), and coordinates of point P.
Each of the next n lines contains two integers — coordinates of the vertices of the polygon in the clockwise or counterclockwise order. It is guaranteed that no three consecutive vertices lie on a common straight line.
All the numbers in the input are integers that do not exceed 1 000 000 in their absolute value.
Output
Print a single real value number — the area of the region that will be cleared. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let’s assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if
![]()
Examples
inputCopy
3 0 0
0 1
-1 2
1 2
outputCopy
12.566370614359172464
inputCopy
4 1 -1
0 0
1 2
2 0
1 1
outputCopy
21.991148575128551812
Note
In the first sample snow will be removed from that area:
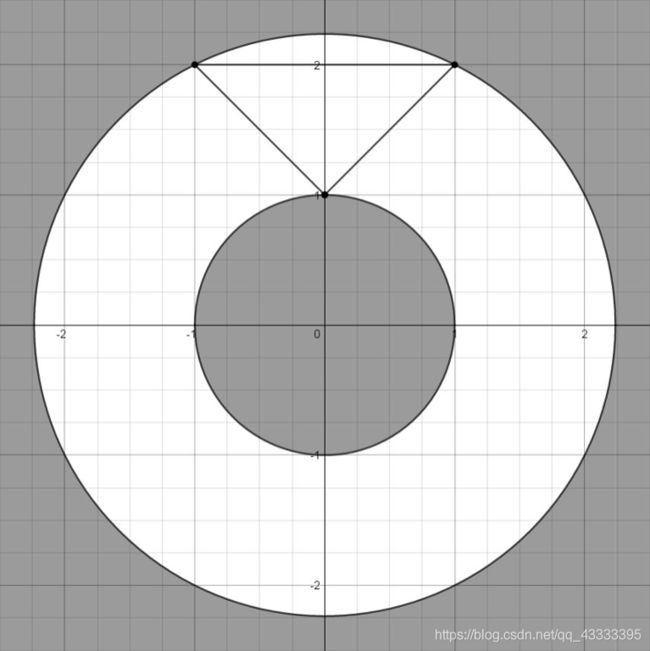
一道几何题
题目的大意是求由点P到正多边形边上任意一点的最大距离为半径的圆的面积减去最小距离为半径的圆的面积,所求即是扫雪机扫过的面积。
对于 最大距离,只需求出每个顶点到P点的距离最大的点即可(不可能是边上的点);
对于 最小距离,点有可能在边上,有可能在顶点上;
所以我们涉及的计算就有:
1.求两点之间的距离。(太简单了~~省略2333)
2.求线段到定点的距离。
我们在在这里假设P为原点(0,0),线段的两端点A.(x1,y1),B.(x2,y2)
那么,

此处若a<=0,说明θ>90,
即最短距离为sqrt(x1x1-y1y1);
若是a>=b,则最短距离为sqrt(x2x2-y2y2);
若0
(上图最后两行(x2-x1)和(y2-y1)为两端点横坐标的距离和纵坐标的距离,c点可以看成等分点)
此时,最短距离为sqrt(xx+yy);
代码实现如下:
double solve(double x2,double y2,double x1,double y1){
double a=(x1-x2)*x1+(y1-y2)*y1;
double b=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
if(a<=0) return x1*x1+y1*y1;
else if(a>=b) return x2*x2+y2*y2;
double r=a/b;
double x=x1+(x2-x1)*r,y=y1+(y2-y1)*r;
return x*x+y*y;
}
题目AC代码如下:
#include
double a=x1[i]*x1[i]+y1[i]*y1[i];
if(maxs<a){
maxs=a;
}
}
x1[n]=x1[0];y1[n]=y1[0]; //最后还要考虑最后一个点和第一个点组成的线段
int flag=0;
for(int i=0;i<n;i++){
mins=min(mins,solve(x1[i],y1[i],x1[i+1],y1[i+1]));
}
double s=pi*(maxs-mins);
printf("%.9f\n",s);
}
第一次写博客,有点小激动QRZ~~
谢谢大家支持(づ ●─● )づ
B. Trees in a Row
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
The Queen of England has n trees growing in a row in her garden. At that, the i-th (1 ≤ i ≤ n) tree from the left has height ai meters. Today the Queen decided to update the scenery of her garden. She wants the trees’ heights to meet the condition: for all i (1 ≤ i < n), ai + 1 - ai = k, where k is the number the Queen chose.
Unfortunately, the royal gardener is not a machine and he cannot fulfill the desire of the Queen instantly! In one minute, the gardener can either decrease the height of a tree to any positive integer height or increase the height of a tree to any positive integer height. How should the royal gardener act to fulfill a whim of Her Majesty in the minimum number of minutes?
Input
The first line contains two space-separated integers: n, k (1 ≤ n, k ≤ 1000). The second line contains n space-separated integers a1, a2, …, an (1 ≤ ai ≤ 1000) — the heights of the trees in the row.
Output
In the first line print a single integer p — the minimum number of minutes the gardener needs. In the next p lines print the description of his actions.
If the gardener needs to increase the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, then print in the corresponding line “+ j x”. If the gardener needs to decrease the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, print on the corresponding line “- j x”.
If there are multiple ways to make a row of trees beautiful in the minimum number of actions, you are allowed to print any of them.
Examples
input
4 1
1 2 1 5
output
2
+ 3 2
- 4 1
input
4 1
1 2 3 4
output
0
题目大意:
给你树的高度,然后让你修改树的高度,使第i+i棵树比第i棵树高k,问最少要修改几棵树。并输出修改的树的修改高度及增加还是减去。
题目思路:
数据很小,直接暴力每一个树为定点,去修改其他树,取出最小修改数的那棵树,之后便以那棵树为中心,去输出修改的关系。
####注意:第一棵树一定要大于0,否则不成立。
代码:
#include I. Marathon
题目链接:http://codeforces.com/group/NVaJtLaLjS/contest/240360/problem/I
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Valera takes part in the Berland Marathon. The marathon race starts at the stadium that can be represented on the plane as a square whose lower left corner is located at point with coordinates (0, 0) and the length of the side equals a meters. The sides of the square are parallel to coordinate axes.
As the length of the marathon race is very long, Valera needs to have extra drink during the race. The coach gives Valera a bottle of drink each d meters of the path. We know that Valera starts at the point with coordinates (0, 0) and runs counter-clockwise. That is, when Valera covers a meters, he reaches the point with coordinates (a, 0). We also know that the length of the marathon race equals nd + 0.5 meters.
Help Valera’s coach determine where he should be located to help Valera. Specifically, determine the coordinates of Valera’s positions when he covers d, 2·d, …, n·d meters.
Input
The first line contains two space-separated real numbers a and d (1 ≤ a, d ≤ 105), given with precision till 4 decimal digits after the decimal point. Number a denotes the length of the square’s side that describes the stadium. Number d shows that after each d meters Valera gets an extra drink.
The second line contains integer n (1 ≤ n ≤ 105) showing that Valera needs an extra drink n times.
Output
Print n lines, each line should contain two real numbers xi and yi, separated by a space. Numbers xi and yi in the i-th line mean that Valera is at point with coordinates (xi, yi) after he covers i·d meters. Your solution will be considered correct if the absolute or relative error doesn’t exceed 10 - 4.
Note, that this problem have huge amount of output data. Please, do not use cout stream for output in this problem.
Examples
input
2 5
2
output
1.0000000000 2.0000000000
2.0000000000 0.0000000000
input
4.147 2.8819
6
output
2.8819000000 0.0000000000
4.1470000000 1.6168000000
3.7953000000 4.1470000000
0.9134000000 4.1470000000
0.0000000000 2.1785000000
0.7034000000 0.0000000000
题目大意:
在正方形左下角的点出发,每次走d(只走正方形的四个边),每走一次记录一次坐标位置,共走n次。
题目思路:
最重要的是得先把x=floor(d/a)%4(我在比赛的时候因为没有这一步wa了),然后就i*x除于a取余数,再判断再哪一条边即可。
代码:
#include
if(k%4==0) printf("%.8f 0.00000000\n",num-(double)a*k);
if(k%4==1) printf("%.8f %.8f\n",a,num-(double)a*k);
if(k%4==2) printf("%.8f %.8f\n",a-num+(double)a*k,a);
if(k%4==3) printf("0.00000000 %.8f\n",a-num+(double)a*k);
}
}
少了上面那步wa的数据点为
Input
1 100000
100000
Output
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.00000000 0.00000000
0.000…
Answer
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000
0.0000000000 0.0000000000…
Checker Log
wrong answer 42949th numbers differ - expected: ‘0.00000’, found: ‘4294983648.00000’, error = ‘4294983648.00000’
B. Inna and New Matrix of Candies
题目链接:http://codeforces.com/group/NVaJtLaLjS/contest/239877/problem/B
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Inna likes sweets and a game called the “Candy Matrix”. Today, she came up with the new game “Candy Matrix 2: Reload”.
The field for the new game is a rectangle table of size n × m. Each line of the table contains one cell with a dwarf figurine, one cell with a candy, the other cells of the line are empty. The game lasts for several moves. During each move the player should choose all lines of the matrix where dwarf is not on the cell with candy and shout “Let’s go!”. After that, all the dwarves from the chosen lines start to simultaneously move to the right. During each second, each dwarf goes to the adjacent cell that is located to the right of its current cell. The movement continues until one of the following events occurs:
some dwarf in one of the chosen lines is located in the rightmost cell of his row;
some dwarf in the chosen lines is located in the cell with the candy.
The point of the game is to transport all the dwarves to the candy cells.
Inna is fabulous, as she came up with such an interesting game. But what about you? Your task is to play this game optimally well. Specifically, you should say by the given game field what minimum number of moves the player needs to reach the goal of the game.
Input
The first line of the input contains two integers n and m (1 ≤ n ≤ 1000; 2 ≤ m ≤ 1000).
Next n lines each contain m characters — the game field for the “Candy Martix 2: Reload”. Character “*” represents an empty cell of the field, character “G” represents a dwarf and character “S” represents a candy. The matrix doesn’t contain other characters. It is guaranteed that each line contains exactly one character “G” and one character “S”.
Output
In a single line print a single integer — either the minimum number of moves needed to achieve the aim of the game, or -1, if the aim cannot be achieved on the given game field.
Examples
input
3 4
GS
G**S
GS
output
2
input
1 3
S*G
output
-1
题目大意:
(题目意思好难读懂QAQ),给你一个矩阵,每一行都有一个S和一个G,然后运动是一起向右运动,直到有一个运动到G或者运动到最右端就算一步。问到全部S到达G要走几步。如果不能实现,就输出-1.
题目思路:
先判断是否有S在G右边的,如果有,则输出-1;然后直接将S到G的距离放进桶里,统计桶中不为0的i值即可。
代码:
#include