线段树·题解报告
线段树·题解报告
参考资料
·课件
线段树 --刘汝佳
统计的力量,线段树全接触 --张昆玮
·Blog
【完全版】线段树
从普通线段树到zkw线段树
[总结][数据结构]ZKW线段树详解
选题目录
· Hdu1166 敌兵布阵(单点更新,区间求和)
· Hdu1754 I Hate It(单点更新,RMQ)
· Hdu3308 LCIS(单点更新,区间并)
· Poj3468 A Simple Problem with Integers(区间加减,区间求和)
· Poj2777 Count Color(区间修改,区间查询,染色)
线段树总结
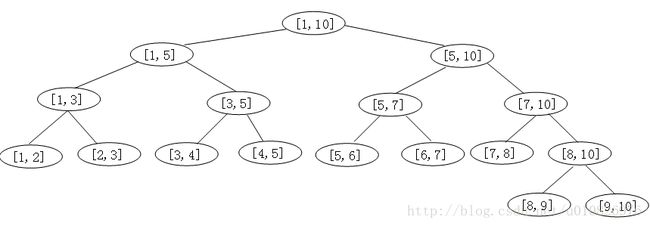
I 普通版递归线段树:
每层都是[a,b]的划分. 记L=b-a, 则共log2L层
任两个结点要么是包含关系要么没有公共部分, 不可能部分重叠
给定一个叶子p, 从根到p路径上所有结点(即p的所有直系祖先)代表的区间都包含点p, 且其他结点代表的区间都不包含点p
给定一个区间[l, r], 可以把它分解为不超过2log2L条不相交线段的并
Lazy思想: 记录有哪些指令, 而不真正执行它们. 等到需要计算的时候再说
根据题目要求确定维护信息和附加信息
具有解决问题的通用性
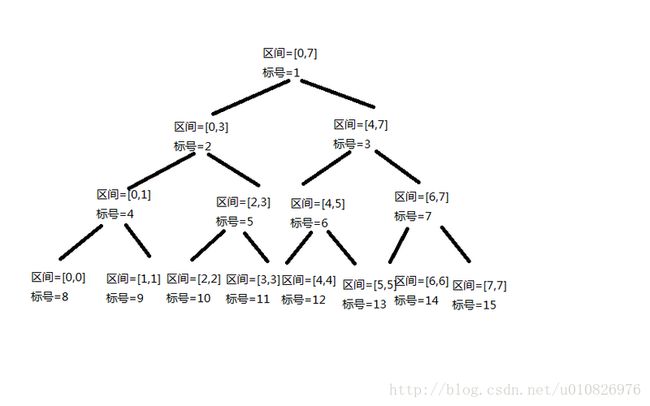
II zkw线段树:
堆式存储,好写,效率较高
自底向上,非递归更新和查询
Lazy标记
题解报告
题目1:Hdu1166 敌兵布阵
题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=1166
题目大意
有N个正整数,对其进行三种操作:
Add i, j 第i个数增加j
Sub i, j 第i个数减去j
Query i, j 查询区间[i, j]中数的和
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),接下来有N个整数。
接下来每行有一条命令,命令有4种形式:
Add i, j 第i个数增加j
Sub i, j 第i个数减去j
Query i, j 查询区间[i, j]中数的和
End 表示结束
每组数据最多有40000条命令
Output
对第i组数据, 首先输出”Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的区间中数的总和,这个数不超过1000000.
思路
线段树的单点修改,区间求和,可以用zkw线段树维护区间和,提高效率,并便于编写代码.
算法步骤
1. 建树
存储空间: T[4 * N], 初始化为0
M: M = 1; while (M < n + 2) M <<= 1;
T[M+1]到T[M+n]: 存n个输入的整数
T[M-1]到T[1]: T[i] = T[2*i] + T[2*i+1];
2. 更新x
更新最下层的数T[x+M], 并自底向上更新其父结点的值
T[i] = T[2*i] + T[2*i+1];
3. 查询[l,r]
令闭区间[l,r]变成(l-1,r+1).
自底向上查询, 从(l = l-1+M, r = r+1+m)开始查询, 如果l
是树中左结点(~l & 1)则加上其右端点值;
如果r是树中右结点(r & 1)则加上其左端点值;
向上查询: l >>= 1; r >>= 1;
当l和r是同层兄弟时结束(l ^ r ^ 1)
算法复杂度
建树O(n), 查询和修改O(logn)
总时间复杂度: O(Alogn) (A为总操作数)
总空间复杂度: O(4 * n)
源程序
/*
* Author: HongSheng Zeng
* Email: [email protected]
* FileName: 1166.cpp
* Creation: 2014/08/31
*/
#include
#include
#include
#include
using namespace std;
const int N = 50000 + 10;
int n, M, i;
int T[4 * N];
void BuildTree()
{
memset(T, 0, sizeof(T));
M = 1;
while (M < n + 2)
M <<= 1;
for (i = M + 1; i <= M + n; ++i)
scanf("%d", &T[i]);
for (i = M - 1; i; --i)
T[i] = T[2 * i] + T[2 * i + 1];
}
int Query(int l, int r)
{
l += M - 1; r += M + 1;
int ans = 0;
while (l ^ r ^ 1) {
if (~l & 1) ans += T[l + 1];
if (r & 1) ans += T[r - 1];
l >>= 1; r >>= 1;
}
return ans;
}
void update(int x, int k)
{
x += M;
T[x] += k;
while (x > 1) {
x >>= 1;
T[x] = T[2 * x] + T[2 * x + 1];
}
}
int main()
{
int t, l, r, x, value;
char ch[10];
scanf("%d", &t);
for (int i = 1; i <= t; ++i) {
scanf("%d", &n);
BuildTree();
printf("Case %d:\n", i);
while (scanf("%s", ch)) {
string s = string(ch);
if (s == "End")
break;
if (s == "Query") {
scanf("%d%d", &l, &r);
printf("%d\n", Query(l, r));
}
if (s == "Add") {
scanf("%d%d", &x, &value);
update(x, value);
}
if (s == "Sub") {
scanf("%d%d", &x, &value);
update(x, -value);
}
}
}
}
评测系统上运行结果
Accepted. 运行时间 312ms, 占用内存1128KB.
题目2:Hdu1754 I Hate It
题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=1754
题目大意
老师需要询问从某某到某某当中,分数最高的是多少,也需要更新某位同学的成绩.
Input
题目包含多组测试,处理到文件结束。
在每个测试的第一行,有两个正整数 N 和 M ( 0
学生ID编号分别从1编到N。
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ,和两个正整数A,B。
当C为'Q'的时候,表示这是一条询问操作,它询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少。
当C为'U'的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
Output
对于每一次询问操作,在一行里面输出最高成绩。
思路
线段树的单点修改,区间求最值(RMQ),可以用zkw线段树维护区间最值,提高效率,并便于编写代码.
算法步骤
1.建树
存储空间: T[4 * N], 初始化为0
M: M = 1; while (M < n + 2) M <<= 1;
T[M+1]到T[M+n]: 存n个输入的整数
T[M-1]到T[1]: T[i] = max(T[2*i], T[2*i+1]);
2.更新x
更新最下层的数T[x+M], 并自底向上更新其父结点的值
T[i] = max(T[2*i], T[2*i+1]);
3. 查询[l,r]
令闭区间[l,r]变成(l-1,r+1).
自底向上查询, 从(l = l-1+M, r = r+1+m)开始查询.
Int ans = 0;
如果l是树中左结点(~l & 1)且其右端点值大于ans,则ans等于其右端点值;
如果r是树中右结点(r & 1)且其左端点值大于ans,则ans等于其左端点值;
向上查询: l >>= 1; r >>= 1;
当l和r是同层兄弟时结束(l ^ r ^ 1)
算法复杂度
建树O(n), 查询和修改O(logn)
总时间复杂度: O(Alogn) (A为总操作数)
总空间复杂度: O(4 * n)
源程序
/*
* Author: HongSheng Zeng
* Email: [email protected]
* FileName: 1754.cpp
* Creation: 2014/09/01
*/
#include
#include
#include
using namespace std;
const int N = 200000 + 10;
int n, m, M, l, r, x, k;
int T[4 * N];
void Build_Tree()
{
memset(T, 0, sizeof(T));
M = 1;
while (M < n + 2)
M <<= 1;
for (int i = M + 1; i <= M + n; ++i)
scanf("%d", &T[i]);
for (int i = M - 1; i; --i)
T[i] = max(T[i * 2], T[i * 2 + 1]);
}
void Update()
{
x += M;
T[x] = k;
while (x) {
x >>= 1;
T[x] = max(T[x * 2], T[x * 2 + 1]);
}
}
int Query()
{
l += M - 1; r += M + 1;
int ans = 0;
while (l ^ r ^ 1) {
if (~l & 1)
ans = max(ans, T[l + 1]);
if (r & 1)
ans = max(ans, T[r - 1]);
l >>= 1; r >>= 1;
}
return ans;
}
int main()
{
while (scanf("%d%d", &n, &m) != EOF) {
Build_Tree();
char ch;
while (m--) {
scanf(" %c", &ch);
if (ch == 'Q') {
scanf("%d%d", &l, &r);
printf("%d\n", Query());
}
else {
scanf("%d%d", &x, &k);
Update();
}
}
}
}
评测系统上运行结果
Accepted. 运行时间 953ms, 占用内存3448KB.
题目3:Hdu3308 敌兵布阵
题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=3308
题目大意
给出一个长度为N(N <= 100000)的数列,然后是两种操作:
U A B: 将第A个数替换为B (下标从零开始)
Q A B: 输出区间[A, B]的最长连续递增子序列
询问的次数m <= 100000。
Input
第一行一个整数T,表示有T组数据。
每组数据第一行有一个整数n和m(0 接下来m行,每行有一条命令,命令有2种形式: U A B (用B替换第A个数, 下标从0开始计数) Q A B (查询区间[A, B]中最长连续子序列的长度) Output 对于每个Q操作,输出结果. 线段树的单点修改,求区间并(查询区间的最长连续子序列)。 Case1: 父节点的左儿子右端点值 >= 父节点的右儿子左端点值 父节点维护区间中的最长连续子序列=max(左儿子最长连续子序列,右儿子最长连续子序列) Case2: 父节点的左儿子右端点值 < 父节点的右儿子左端点值 父节点维护区间中的最长连续子序列=max(左儿子最长连续子序列,右儿子最长连续子序列,左儿子维护区间中以其右端点结束的最长连续子序列+右儿子维护区间中以其左端点开始的最长连续子序列) 故线段树中需要维护区间的最长连续子序列(smax),区间以左端点开始的最长连续子序列(lmax),和区间以右端点结束的最长连续子序列(rmax).维护信息较复杂且查询时自顶向下比较方便,故用普通版的递归线段树. 0. 信息向上更新 通过Up操作(详见源代码)将父节点的左右儿子的smax,lmax,rmax信息更新到父节点。 1.建树 struct node { int l, r, lmax, rmax, smax; } tree[3 * N]; 从上往下建树,然后从下往上更新维护信息. 2.更新x 从上往下,确定x,并更新其值,然后通过Up操作往上更新维护信息。 3. 查询[l,r] 从上往下递归查询区间,跨区间时需合并结果。 建树O(n), 查询和修改O(logn) 总时间复杂度: O(Alogn) (A为总操作数) 总空间复杂度: O(3 * n) /* * Author: HongSheng Zeng * Email: [email protected] * FileName: 3308.cpp * Creation: 2014/09/10 */ #include #include #include using namespace std; const int N = 100000 + 10; int num[N]; struct node { int l, r, lmax, rmax, smax; } tree[3 * N]; void Up(int x) { int l = tree[x].l, r = tree[x].r; int mid = (l + r) / 2; tree[x].lmax = tree[x * 2].lmax; tree[x].rmax = tree[x * 2 + 1].rmax; tree[x].smax = max(tree[x * 2].smax, tree[x * 2 + 1].smax); if (num[mid] < num[mid + 1]) { if (tree[x].lmax == (mid - l + 1)) tree[x].lmax += tree[x * 2 + 1].lmax; if (tree[x].rmax == (r - mid)) tree[x].rmax += tree[x * 2].rmax; tree[x].smax = max(tree[x].smax, tree[x * 2].rmax + tree[x * 2 + 1].lmax); } } void BuildTree(int x, int l, int r) { tree[x].l = l; tree[x].r = r; if (l == r) { tree[x].lmax = tree[x].rmax = tree[x].smax = 1; return; } int mid = (l + r) / 2; BuildTree(x * 2, l, mid); BuildTree(x * 2 + 1, mid + 1, r); Up(x); } void Update(int x, int k) { if (tree[x].l == tree[x].r) return; int l = tree[x].l , r = tree[x].r; int mid = (l + r) / 2; if (k <= mid) Update(x * 2, k); else Update(x * 2 + 1, k); Up(x); } int Query(int x, int l, int r) { if (tree[x].l == l && tree[x].r == r) return tree[x].smax; int mid = (tree[x].l + tree[x].r) / 2; if (r <= mid) return Query(x * 2, l, r); else if (l > mid) return Query(x * 2 + 1, l, r); else { int ans = max(Query(x * 2, l, mid), Query(x * 2 + 1, mid + 1, r)); if (num[mid] < num[mid + 1]) { ans = max(ans, min(tree[x * 2].rmax, mid - l +1) + min(tree[x * 2 + 1].lmax, r - mid)); } return ans; } } int main() { int t, l, r, index, k, n, m; char ch; scanf("%d", &t); while (t--) { scanf("%d%d", &n, &m); for (int i = 1; i <= n; ++i) scanf("%d", &num[i]); BuildTree(1, 1, n); while (m--) { scanf(" %c", &ch); if (ch == 'Q') { scanf("%d%d", &l, &r); ++l; ++r; printf("%d\n", Query(1, l, r)); } else { scanf("%d%d", &index, &k); ++index; num[index] = k; Update(1, index); } } } } Accepted. 运行时间 484ms, 占用内存5832KB. 题目4:Poj3468 A Simple Problem with Integers http://poj.org/problem?id=3468 有N个正整数,对其进行两种操作: ‘Q a b ’ 询问a~b这段数的和 ‘C a b c’ 把a~b这段数都加上c Input 第一行两个整数N,Q, 1 ≤ N,Q ≤ 100000. 接下来有N个整数:A1, A2, ... , AN, -1000000000 ≤ Ai ≤ 1000000000. 接下来有Q行,每行有一条命令,命令有2种形式: "C a b c" Aa, Aa+1, ... , Ab 的值都加上c, -10000 ≤ c ≤ 10000. Output 对于每个Query询问,输出一个数并回车,表示询问的区间中数的总和. 线段树的区间加,区间求和,使用线段树+lazy标记,因为只需要维护区间和,从下往上也可以便利地查询,所以用zkw线段树。 1. 建树 存储空间: T[4 * N], 初始化为0 标记空间: mark[4 * N], 初始化为0, mark[i]表示i结点以下所有结点更新值之和,当mark[i]不为0 时说明结点i的更新信息还没更新到其子结点. M: M = 1; while (M < n + 2) M <<= 1; h: 树的高度 T[M+1]到T[M+n]: 存n个输入的整数 T[M-1]到T[1]: T[i] = T[2*i] + T[2*i+1]; 2. down(x)操作 标记下传, 沿着根结点到x的线路,父结点的标记信息更新到其子结点,并清空父结点的标记 信息. 3. up(x)操作 沿着x到根结点的路线,用子结点的维护信息更新父结点的维护信息. 4.更新[l, r], +k l += M - 1; r += M + 1; 标记下传down(l), down(r); lazy更新结点: 如果l是树中左结点(~l & 1)则更新其右端点值+k,并更新其标记值+k; 如果r是树中右结点(r & 1)则更新其左端点值+k,并更新其标记值+k; 向上更新: l >>= 1; r >>= 1; 当l和r是同层兄弟时结束(l ^ r ^ 1) 对l父结点和r父结点进行up操作 5. 查询[l,r] l += M - 1; r += M + 1; 标记下传down(l), down(r) 查询: 如果l是树中左结点(~l & 1)则加上其右端点值; 如果r是树中右结点(r & 1)则加上其左端点值; 向上查询: l >>= 1; r >>= 1; 当l和r是同层兄弟时结束(l ^ r ^ 1) 建树O(n), 查询和修改O(logn) 总时间复杂度: O(Alogn) (A为总操作数) 总空间复杂度: O(4 * n) /* * Author: HongSheng Zeng * Email: [email protected] * FileName: 3468.cpp * Creation: 2014/09/03 */ #include #include #include using namespace std; const int N = 100000 + 10; int n, q, M, h, l , r, ll, rr, t; long long k; long long T[4 * N]; long long mark[4 * N]; void Build_Tree() { memset(T, 0, sizeof(T)); memset(mark, 0, sizeof(mark)); int i; M = 1; h = 0; while (M < n + 2) { M <<= 1; ++h; } for (i = M + 1; i <= M + n; ++i) scanf("%lld", &T[i]); for (i = M - 1; i; --i) T[i] = T[i * 2] + T[2 * i + 1]; } void down(int x) { for (int i = h; i; --i) if (mark[t = x >> i]) { mark[t] >>= 1; mark[t << 1] += mark[t]; mark[t * 2 + 1] += mark[t]; T[t << 1] += mark[t]; T[t * 2 + 1] += mark[t]; mark[t] = 0; } } void up(int x) { while (x) { T[x] = T[x << 1] + T[x * 2 + 1]; x >>= 1; } } void Update() { l += M -1; r += M + 1; ll = l >> 1; rr = r >> 1; down(l); down(r); while (l ^ r ^ 1) { if (~l & 1) { T[l + 1] += k; mark[l + 1] += k; } if (r & 1) { T[r - 1] += k; mark[r - 1] += k; } k <<= 1; l >>= 1; r >>= 1; } up(ll); up(rr); } long long Query() { long long ans = 0; l += M - 1; r += M + 1; down(l); down(r); while (l ^ r ^ 1) { if (~l & 1) ans += T[l + 1]; if (r & 1) ans += T[r - 1]; l >>= 1; r >>= 1; } return ans; } int main() { scanf("%d%d", &n, &q); Build_Tree(); char ch; for (int i = 0; i < q; ++i) { scanf(" %c%d%d", &ch, &l, &r); if (ch == 'Q') { printf("%lld\n", Query()); } else { scanf("%lld", &k); Update(); } } } Accepted. 运行时间 2219ms, 占用内存6952KB. 题目5:Poj2777 Count Color http://poj.org/problem?id=2777 有一个区间[1,L],被分成L段,标记为1,2...L;最多有T种颜色。有两种操作,一种是对某一个区间段染上某一种颜色,一种是询问该区间有多少种不同的颜色。整个区间刚开始为1. Input 第一行L (1 <= L <= 100000), T (1 <= T <= 30) 和 O (1 <= O <= 100000). 接下来O行,每行有一条命令,命令有2种形式: C A B C (给A到B区间染上C色) Q A B (查询区间[A, B]有多少种不同的颜色) Output 对于每个Q操作,输出结果. 线段树的染色问题,区间修改,区间查询. 结点维护信息: 0-非纯色; 非0-纯颜色. 当结点为非纯色时,才需要访问其子结点查询. 自上向下查询比较方便,用普通版递归线段树. 1.建树 struct node { int l, r, color; } tree[3 * N]; 从上往下建树,颜色初始化为1. 2.更新[l, r] 区间颜色标记下放,从上往下lazy更新. 3. 查询[l,r] 从上往下递归查询,当结点为非纯色时,才向下查询其子结点。 建树O(n), 查询和修改O(logn) 总时间复杂度: O(Alogn) (A为总操作数) 总空间复杂度: O(3 * n) /* * Author: HongSheng Zeng * Email: [email protected] * FileName: 2777.cpp * Creation: 2014/09/07 */ #include #include #include using namespace std; const int N = 100000 + 10; struct node { int l, r, color; } tree[3 * N]; bool mark[35]; void Build_Tree(int x, int l, int r) { tree[x].l = l; tree[x].r = r; tree[x].color = 1; if (l == r) return; int mid = (l + r) / 2; Build_Tree(x * 2, l, mid); Build_Tree(x * 2 + 1, mid + 1, r); } void Update(int x, int l, int r, int color) { if (tree[x].l == l && tree[x].r == r) { tree[x].color = color; return; } // Down if (tree[x].color != 0 && tree[x].color != color) { tree[x * 2].color = tree[x].color; tree[x * 2 + 1].color = tree[x].color; tree[x].color = 0; } int mid = (tree[x].l + tree[x].r) / 2; if (r <= mid) Update(x * 2, l, r, color); else if (l > mid) Update(x * 2 + 1, l, r, color); else { Update(x * 2, l, mid, color); Update(x * 2 + 1, mid + 1, r, color); } } void Query(int x, int l, int r) { if (tree[x].color > 0) { mark[tree[x].color] = true; return; } int mid = (tree[x].l + tree[x].r) / 2; if (r <= mid) Query(x * 2, l, r); else if (l > mid) Query(x * 2 + 1, l, r); else { Query(x * 2, l, mid); Query(x * 2 + 1, mid + 1, r); } } int main() { int L, T, O, l, r, k; char ch; scanf("%d%d%d", &L, &T, &O); memset(mark, false, sizeof(mark)); Build_Tree(1, 1, L); while (O--) { scanf(" %c%d%d", &ch, &l, &r); if (l > r) { l = l ^ r; r = l ^ r; l = l ^ r; } if (ch == 'C') { scanf("%d", &k); Update(1, l, r, k); } else { memset(mark, false, sizeof(mark)); Query(1, l, r); int sum = 0; for (int i = 1; i <= T; ++i) if (mark[i]) ++sum; printf("%d\n", sum); } } } Accepted. 运行时间 422ms, 占用内存3764KB.思路
算法步骤
算法复杂度
源程序
评测系统上运行结果
题目链接
题目大意
"Q a b" 查询区间Aa, Aa+1, ... , Ab的值的总和.思路
算法步骤
算法复杂度
源程序
评测系统上运行结果
题目链接
题目大意
思路
算法步骤
算法复杂度
源程序
评测系统上运行结果