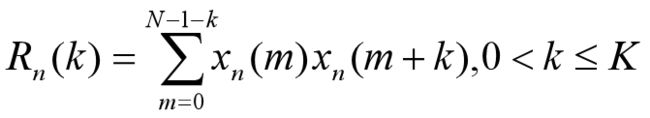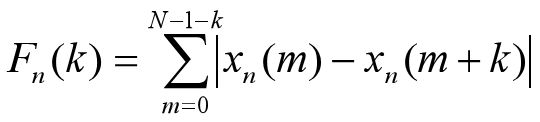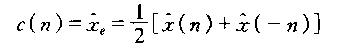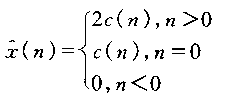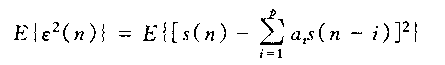语音信号处理第三章:
语音信号处理第二章
语音信号处理第三章
语音信号处理第四章
语音信号处理第五章
语音信号处理第七章
语音信号处理第九章
语音信号处理第十章
语音信号处理第十二章
文章目录
- 1.数字化和预处理
- 1.1.数字化
- 1.1.1.预滤波
- 1.1.2.A/D变换
- 1.2.预处理
- 1.2.1.预加重
- 1.2.2.加窗
- 1.2.3.分帧
- 2.时域分析语音信号
- 2.1.短时能量:
- 2.2.短时过零率
- 2.3.短时自相关函数
- 3.频域分析语音信号
- 4.倒谱分析语音信号
- 4.1.倒谱的处理过程
- 4.2.基于倒谱的基音周期检测:
- 4.3.MFCC
- 5.线性预测分析语音信号
- 5.1.LPC谱估计:
- 6.基音周期估计
- 6.1.自相关函数法ACF
- 6.2.倒谱法
- 6.3.后处理
- 7.共振峰估计
- 7.1.倒谱法
- 7.2.LPC法
1.数字化和预处理
数字化:带通滤波、放大及增益控制(AGC)、反混叠滤波、采样、A/D变换、PCM编码
预处理:预加重、加窗和分帧
1.1.数字化
1.1.1.预滤波
用途:
(1)抑制输入信号各频域分量中频率超出fs/2的所有分量(fs为采样频率),以防止混叠干扰
(2)抑制50Hz的电源工频干扰
预滤波是一个带通滤波器,范围是60~3400Hz,采样频率是8kHz
1.1.2.A/D变换
用途:将语音信号转换为二进制码
A/D变换中要对信号进行量化。量化不可避免地会产生误差,量化后的信号值与原信号值之间的差值称为量化误差,又称为量化噪声。量化间隔越小,量化噪声也就越小。
若信号波形的变化足够大,或量化间隔Δ足够小时,可以证明量化噪声符合具有下列特征的统计模型:
①它是平稳的白噪声过程
②量化噪声与输入信号不相关
③量化噪声在量化间隔内均匀分布,即具有等概率密度分布
每增加一个量化位数,量化信噪比增加6dB
并不是量化信噪比越高越好,还要考虑带宽能否承受
1.2.预处理
由于语音信号是一个非平稳过程,需要分帧成为短时平稳过程,才能使用处理平稳信号的技术
1.2.1.预加重
目的:提升高频部分,使信号的频谱变得平坦,保持在低频到高频的整个频带中,能用同样的信噪比求频谱,以便于频谱分析或声道参数分析。
1.2.2.加窗
原理:分帧是用可移动的有限长度窗口进行加权的方法来实现的,也就是用定长的窗函数ω(n)来乘s(n),从而形成加窗语音信号sω(n)=s(n)ω(n)
窗的类型:
在语音信号数字处理中常用的窗函数是矩形窗和汉明窗等
汉明窗的主瓣宽度比矩形窗大一倍,即带宽约增加一倍。同时,其带外衰减也比矩形窗大一倍多,具有频谱泄露小的优点。矩形窗带外衰减很小,有较大的上下冲,会导致Gibbs效应,不能准确反映语音音素的频谱。矩形窗的谱平滑性能较好,但损失了高频成分,使波形细节丢失;而汉明窗则相反,从这一方面来看,汉明窗更适合频域分析,矩形窗更适合时域分析
窗长N:
采样周期TS = 1/fS
窗口长度N、采样频率fS和频率分辨率Δf之间存在下列关系:
Δf = fS/N
可见,采样频率一定时,Δf随窗口长度N的增加而减小,即频率分辨率Δf相应得到提高,但同时时间分辨率(1/Δf)降低,因此要合理选择窗长N:
1)N太大时,加窗相当于很窄的低通滤波器,反映波形细节的高频部分被滤除,短时能量随时间变化很小(过于平滑)。N太小时,短时能量变化急剧(不够平滑)。
2)一个语音帧内应包括2个以上的基音周期,通常在fS=10kHz时,N折中选择为100~200点合适(即10 ~ 20ms的持续时间)。
1.2.3.分帧
一般来说每秒的帧数约为33~100帧
分帧一般要采用交叠分段的方法,目的是为了使帧与帧之间平滑过渡,保持其连续性。
帧重叠:前一帧和后一帧的交叠部分
帧移:前后移动的距离。
帧长:一帧的长度
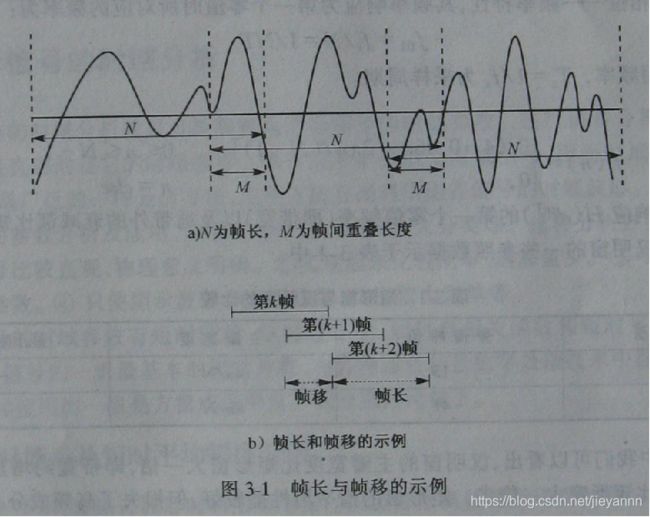
原语音信号长度L、帧数X、帧长N、帧移M的关系:
L=N+(X-1)M。一般来说M=N/2
2.时域分析语音信号
时域分析的优点
①表示语音信号比较直观、物理意义明确。
②实现起来比较简单、运算量少。
③可以得到语音的一些重要的参数。
④只使用示波器等通用设备,使用较为简单等。
时域参数:假设第n帧语音信号xn(m),m=[0,N-1]
2.1.短时能量:

用途:
(1)从较小的背景噪声中找出语音信号,或者区分无声和有声的分界
(2)区分浊音段和清音段,因为浊音的短时能量比清音大
缺点:对高电平非常敏感:根据短时能量公式,假如某个采样点出现很高的电平,那么短时能量会特别高,从而无法准确反映该帧的能量
改进:短时平均幅度函数
2.2.短时过零率
过零率:样本改变符号的次数。
原理:
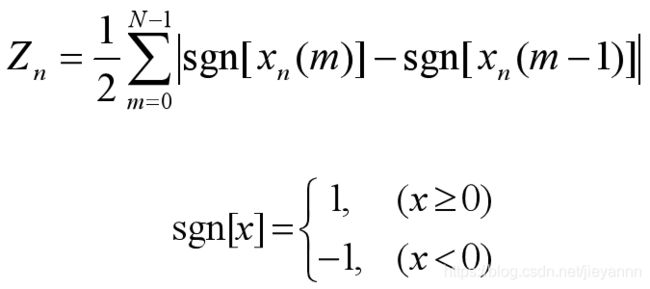
用途:
(1)可用于区分浊音和清音,因为浊音的短时过零率比清音低
高频意味着高的平均过零率。浊音具有较低的过零率,因为声门波引起谱的高频跌落,导致其语音能量集中在较低频率;清音的过零率会更高,因为清音是噪声,多数能量出现在较高频率(参考第一章)
(2)从较大的背景噪声中找出语音信号,可用于判断寂静无声段和有声段的起点和终点位置(即端点检测)
基于短时能量和短时过零率的端点检测方法:(假设无声段S、清音段U、浊音段V)
方法一:双门限法
方法二:
X=S或U或V。后验概率最大者即为判别结果。
缺点:在以某些音为开始或结尾时,如当弱摩擦音(如[f]、[h]等音素)、弱爆破音(如[p]、[t]、[k]等音素)为语音的开头或结尾;以鼻音(如[ng]、[n]、[m]等音素)为语音的结尾时,只用其中一个参量来判别语音的起点和终点是有困难的,进行端点检测时必须同时使用平均过零率和平均能量两个参数。
2.3.短时自相关函数
这里K是最大的延迟点数
用途:
(1)对浊音语音可以用自相关函数求出语音波形序列的基音周期
检测方法:找到自相关函数的第一个峰值的位置,用采样频率除以峰值位置(位于第几个点),就是基音频率。
估计基音周期时,如果窗长不够,会导致第一个峰值的位置不能与基音周期吻合。窗长至少应大于两个基音周期。而查阅资料得知,男性女性儿童等全部人群的基音频率的极限范围在50 ~ 500Hz,也就是基音周期极限范围为2 ~ 20ms。因此只用于估计基音周期时,窗长N应选得大于40ms比较合适。如果既要用于检测基音周期,又要用于短时能量,则折中选择10~20ms。实验中,测出的普通男性基音频率在100 ~ 300Hz之间,即基音周期在3 ~ 10ms之间,此时窗长选择10 ~ 20ms够用。
(2)语音信号的线性预测分析
缺点:运算量很大,因为乘法运算所需要的时间较长。利用快速傅里叶变换(FFT)等简化计算方法都无法避免乘法运算
改进:短时平均幅度差函数(ADMF)
短时平均幅度差函数AMDF
原因:如果信号是完全的周期信号(设周期为Np),则相距为周期的整数倍的样点上的幅值是相等的,差值为零
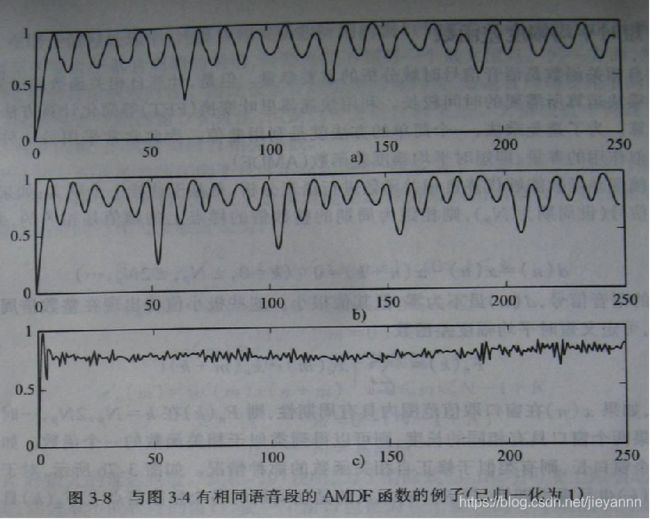
原理:
a)和b)是浊音语音的AMDF;c)是清音语音的AMDF
a)和b)中,局部的最小值之间的距离就是周期,而浊音信号才有明显周期。
要注意的是,短时自相关函数是在峰值处取基音周期,而短时平均幅度差函数是在谷值处取基音周期
3.频域分析语音信号
常用的频域分析方法有带通滤波器组法、傅里叶变换法、线性预测法等
应该用短时傅里叶变换对语音信号的频谱进行分析,相应的频谱称为“短时谱”。
对第n帧语音信号xn(m)进行傅里叶变换(离散时域傅里叶变换,DTFT),可得到短时傅里叶变换,其定义如下:
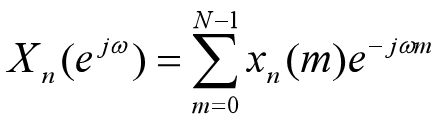
4.倒谱分析语音信号
原因:语音信号可以看作是声门激励信号和声道冲激响应信号的卷积
原理:
求取语音倒谱特征参数–>同态处理–>将卷积变换为求和–>将声门激励和声道响应分离–>求得声道共振特征和基音周期

同态信号处理就是将非线性问题转化为线性问题的处理方法
4.1.倒谱的处理过程
x(n)(时)–(傅里叶变换)–>X(ejω)(频)–>取对数–(傅里叶逆变换)–>x^(n)(时)
这个x^(n)就是倒谱
复倒谱和倒谱的性质:
(1)DTFT后的X(ejω)有幅度和相位,如果只对幅度取对数,得到的就是倒谱;对整体取对数,得到的就是复倒谱
(2)在倒谱情况下,一个序列经过正逆两个特征系统变换后,不能还原成自身,因为在计算倒谱的过程中,只取幅度,而将序列的相位信息丢失了。
(3)已知一个实数序列x(n)的复倒谱x^(n),可用以下等式求x(n)的倒谱c(n)(4)已知一个实数序列x(n)的倒谱c(n),如果用以下等式求复倒谱x^(n),x(n)必须满足以下条件:
复倒谱分析中,取对数时进行的是复对数运算,这时存在相位多值性问题,称为“相位卷绕”。
避免相位卷绕的方法有微分法,最小相位信号法
4.2.基于倒谱的基音周期检测:
原理:
声门激励信号序列复倒谱的性质:
(1)如果是浊音,则为周期冲激序列,周期等于原本的基音周期
(2)振幅衰减序列
声道响应序列复倒谱的性质:
(1)双边序列
(2)振幅衰减序列,而且大部分集中于原点附近
因此,浊音帧的倒谱能明显看到声门激励信号和声道响应的倒谱,而清音帧只能看到声道响应的倒谱

上图中,右边的小图里面pitch peak峰与峰之间的距离就是基音周期。
倒谱基音周期检测中,窗函数应选择汉明窗。矩形窗会导致基音峰值变得不清晰甚至消失,如上图右上角所示。
4.3.MFCC
MFCC 参数提取流程:
语音信号经过预加重、加窗分帧处理后变为短时信号,将短时信号做离散傅里叶变换。然后:

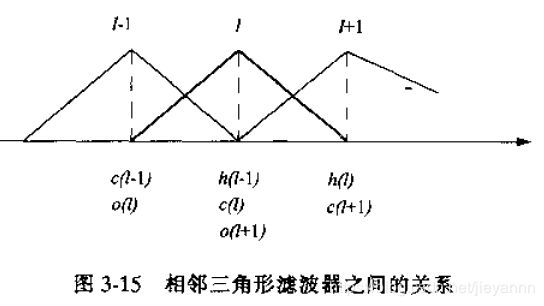
L常取10~15
5.线性预测分析语音信号
线性预测分析的基本思想是:用过去p个样本值来预测现在或未来的样本值
原理:由该时刻过去的p个点的值加权累加,得到该时刻的预测值。
只选用过去的点是因为声道传递函数就是全极点模型。
目标:找到一组共p个加权值,使得预测值和实际值误差最小,这些加权值被称为线性预测系数。
用途:这组预测系数反映了语音信号的特性,可用于语音识别、语音合成等。以LPC谱估计介绍线性预测的用途:
5.1.LPC谱估计:
原理:得到预测系数ai后,将这组预测系数组成的序列进行傅里叶变换,作为分母;利用预测系数计算模型的增益G,作为分子。两者组合得到其对应的语音产生模型的频率响应,称为LPC谱。
特点:在信号能量较大的区域(即接近谱的峰值处)LPC谱和信号谱很接近,而在信号能量较低的区域(即接近谱的谷值处)相差比较大
实现:

问题是,想要直接解出等式(3-106)是很麻烦的,于是就有了下列算法
求解:自相关法:

只要解出方程(3-113)(又称为Yule-Wslker方程),就能得到预测系数ai
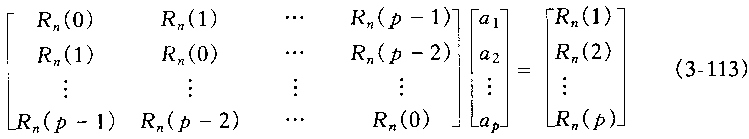
解(3-113)方程使用的是Durbin快速递推算法。过程如下:
语音信号处理中,p一般选在8~14之间。
6.基音周期估计
基音是指发浊音时声带振动所引起的周期性,而基音周期是指声带振动频率的倒数
基音周期描述了语音激励源的一个重要特征
常用基音检测算法:
自相关函数(ACF)法、峰值提取算法(PPA)、平均幅度差函数(AMDF)法、并行处理技术、倒谱法、SIFT、谱图法、小波法等等
要准确估计基音周期,除了核心算法思想(例如小波法、自相关法),预处理(例如中心削波)和后处理(例如平滑处理)也很重要。
6.1.自相关函数法ACF
原理:浊音信号的自相关函数在基音周期的整数倍位置上出现峰值;而清音的自相关函数没有明显的峰值出现。因此检测是否有峰值就可判断是清音或浊音,检测峰值的位置就可提取基音周期值
步骤:
(1)预处理:排除干扰,找到基音周期对应的真正的峰值位置
1)使用窗长约为10~20ms的矩形窗进行加窗
2)加带通滤波器60~900Hz,或者进行非线性变换
900Hz是因为既能除去大部分共振峰的影响,又能当基音频率为最高450Hz时仍能保留其一二次谐波。60Hz是为了抑制50Hz的电源干扰。
非线性变换的目的是排除干扰,找到真正的基音周期第一个峰值
非线性变换的方法:中心削波函数或三电平中心削波函数
中心削波函数是指去除中间部分,只保留语音信号高幅度和低幅度部分,因为高幅度部分包含大量基音信息,低幅度部分包含大量共振峰信息。
(2)求自相关函数
(3)检测峰值的位置,就是基音周期值
AMDF法同理,只不过是改成检测谷值
6.2.倒谱法
步骤:
(1)原始信号分帧加窗
(2)对分帧语音进行LPC分析,得到预测系数a,并利用a的傅里叶变换和预测增益G构成逆滤波器
(3)将分帧语音通过(2)得到的逆滤波器滤波,获得预测信号
(4)对预测信号进行DFT、取对数的处理后,进行低通滤波处理,或者将处理后的信号的高频分量置零
(5)进行IDFT,得到原信号的倒谱
(6)检测倒谱中的峰值,所处位置就是对应的基音周期
6.3.后处理
原因:无论采用哪一种基音检测算法都可能产生基音检测错误,使求得的基音周期轨迹中有一个或几个基音周期估值偏离了正常轨迹。这种偏离点为基音轨迹的“野点”
原理:由于短时平稳性,声音在短时间内的频率变化不会太大,这有助于判断某点是否为“野点”。
步骤
为了去除这些野点,可以后处理,采用各种平滑算法,其中最常用的是中值平滑算法和线性平滑算法。
中值平滑处理:每次取3/5个点,用这3/5个点的中值作为输出,从而去除少量野点
线性平滑处理:每次取3/5个点,用这3/5个点加权输出
7.共振峰估计
声道可以看成是一根具有非均匀截面的声管,在发音时起共鸣器的作用。当准周期脉冲激励进入声道时会引起共振特性,产生一组共振频率,称为共振峰频率或简称共振峰
共振峰描述了声道的一个重要特征
共振峰参数:共振峰频率和频带宽度,它是区别不同韵母的重要参数
共振峰通常取前两个
7.1.倒谱法
原因:
可以直接DFT,根据DFT谱来提取共振峰参数。但是由于最大值出现在谐振频率上,测量误差较大。因此,可以使用同态滤波得到平滑的谱再检测。将倒谱DFT,用得到的DFT谱来检测共振峰,比起直接DFT谱更准确
步骤

在最后一步DFT处理以后,检测频谱H(K)中的峰值点,所在位置就是共振峰频率
注:
w(n):加窗使用的窗函数
l(n):低时窗,用于从倒谱中截取出声道响应部分
优点:倒谱法得到的频谱曲线波动较小,所以估计共振峰参数的效果比较好
缺点:运算量太大
7.2.LPC法
步骤:
(1)原始信号分帧加窗
(2)对分帧语音进行LPC分析,得到预测系数a
(3)对预测系数a补0,形成N点序列,然后进行N点DFT,得到对应的频率响应A
(4)找到频率响应A的谷值点,所在位置就是共振峰频率
注:此处LPC法依照的是《语音信号处理》赵力版本p78的内容,可能与网络上的LPC法存在出入。