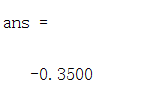台湾国立大学郭彦甫Matlab教程笔记(20) root finding(numeric)
台湾国立大学郭彦甫Matlab教程笔记(20) root finding(numeric)
symbolic vs. numeric符号法和数值法的区别对比
symbolic
1)advantages
analytical solutions解析解
let you intuit凭感觉知道 things about solution form凭感觉知道解的形式
2)disadvantages
sometimes can’t be solved有时候解不出来
can be overly complicated过于复杂
numeric
1)advantages
always get a solution通常有解
can make solutions accurate 解很准确
easy to code 代码简单
2)disadvantages
hard to extract a deeper understanding
很难有更深的理解
这几课的第二单元
numeric solver数值解
如何运用matlab中的内建函数
回顾一下function handle @
这里为什么还要复习function handle 呢?因为待会讲的numeric solver 需要用到function handle
作用:a handle is a function pointer
pass functions to other functions
举例子:一个函数的输入是一个函数
下面是一个xy_plot()函数,可以绘制图像
function [y]=xy_plot(input,x)
y=input(x);
plot(x,y,'r--');
xlabel('x');
ylabel('function(x)');
end
try:xy_plot(@sin,0:0.01:2pi);%画出sin()函数的图像
xy_plot(@atan,0:0.01:2pi);%画出arctan()函数的图像
画出来的arctan(x)的图像:

我们开始讲numeric root solver 根数值求解
fsolve()函数的使用
a numeric root solver
例程:
f2= @(x) (1,2*x+0.3+x.*sin(x));
这个叫做inline function 内联函数

fsolve(f2,0)%f2是一个函数句柄, 0是初始猜测,然后fsolve会帮我们解这个方程f(x)=0
代码:
f2= @(x) (1,2*x+0.3+x.*sin(x));
fsolve(f2,0)%
function tolerance 什么意思呢? 函数容差
计算出来
练习题:解二元方程组,使用数值解法fsolve
查资料
在matlab中输入 help fsolve,然后进入 fsolve参考页,学习一下fsolve 的用法
看下面的 二元非线性方程组的求解例题
题目:两个变量的方程组如下

求解过程:
【1】写一个函数,这个函数函数体中是两个代求的方程,然后保存为.m文件
【2】用句柄@调用函数
【3】給初值,用fsolve()函数解决。
(来源:matlab官方文档)
我的求解过程:
root2d.m文件中:
function F= root2d(x)%函数名是root2d
F(1)=2x-y-exp(-x);%函数体是两个代求方程
F(2)=-x+2y-exp(-y);
end
上面代码是错误的,需要用x(1)和x(2)来表示x和y,不能直接用y。
代码修改为:
function F= root2d(x)%函数名root2d
F(1)=2x(1)-x(2)-exp(-x(1));%用x(1) and x(2)表示不同的 变量,比如x,y
F(2)=-x(1)+2x(2)-exp(-x(2));
end
function F= root2d(x)%函数名root2d
F(1)=2*x(1)-x(2)-exp(-x(1));%用x(1) and x(2)表示不同的 变量,比如x,y
F(2)=-x(1)+2*x(2)-exp(-x(2));
end
调用代码:
fun=@root2d;%函数句柄调用root2d函数
x0=[-5,-5];%初始值
fsolve(fun,x0)
fun=@root2d;%函数句柄调用root2d函数
x0=[-5,-5];%初始值
fsolve(fun,x0)
另外一个 numeric root solver
fzero()函数
find the zero if and only if the function crosses the x-axis
fzero 需要注意,函数必须穿过x轴才有解。如果和x轴相切而不穿过,则fzero解不出来。
举例:求 f=x^2的根
例程:下面就是解不出来
f=@(x) x.^2;
fzero(f,0.1)%f:function handle ; 0.1:initial guess
f=@(x) x.^2;
fzero(f,0.1)%f:function handle ; 0.1:initial guess
运行结果:

可以用fsolve(f,0.1)解出值
但是精度不够
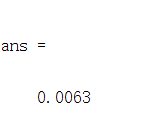
然后 fsolve() 和 fzero() 函数有进阶的用法
options
用法:
options =optimset(‘maxiter’,1e3,‘tolfun’,1e-10);
options =optimset('maxiter',1e3,'tolfun',1e-10);
使用一个function : optimset () option set 可以使算出来的数值精度更高

例程:
f=@(x) x.^2;
options =optimset(‘maxiter’,1e3,‘tolfun’,1e-10);
fsolve(f,0.1,options)
fzero(f,0.1,options)
f=@(x) x.^2;
options =optimset('maxiter',1e3,'tolfun',1e-10);
fsolve(f,0.1,options)
fzero(f,0.1,options)
在误差为1*10的-10次方的情况下,求得数值解为
finding roots of polynomials:root()函数
举例:

代码:
roots([1,-3.5,2.75,2.125,-3.875,1.25])
得到多项式的解:

练习题
使用roots()这个函数求解下面多项式的解

代码:roots([1,-6,-12,81])
得到的多项式的解

两种主要的数值求根方法:
一种是有区间包夹的:括号法
另一种是没有区间包夹的,代表是牛顿法
数值方法停止运算需要两个标准要满足:要么是精度够了,要么是运算次数达到了

下面看第一种method
bisection method (bracketing)括号法
现在进行到这里
bisection method (bracketing)
用二分法来找
lowerbond upperbond
iteration 递归,迭代
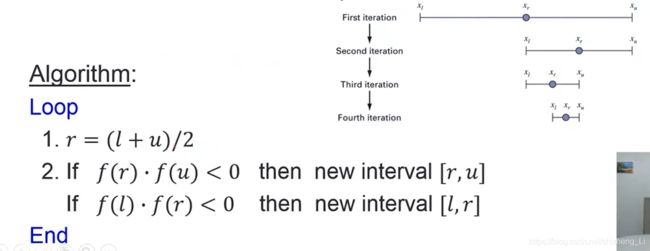
整个二分法的迭代过程:
其中,r是区间中点,然后不断循环,区间不断减半逼近根植
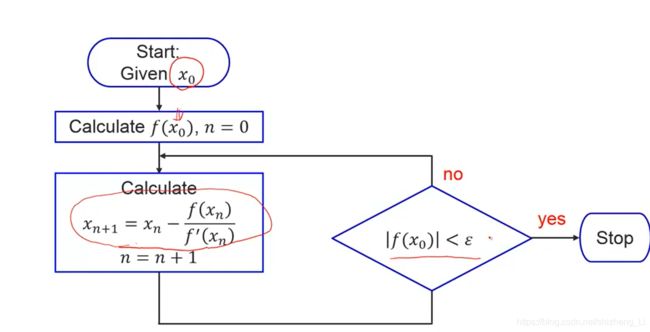
二分算法流程图
bisection algorithm flowchart

下面看另外一个方法牛顿法
newton-raphson method(open)牛顿法
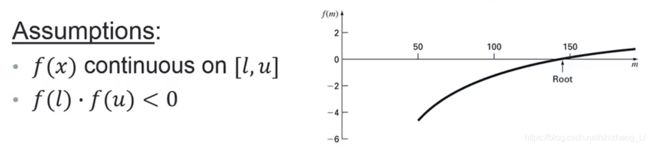
适用条件
1)函数连续
2)导数已知
牛顿法思路:过f(x0)一点作切线,交x轴交点为x1,然后找到函数值f(x1),过该点再作切线,接着交x轴,不停迭代下去。知道找到曲线与x轴交点(方程的根)为止

下面我们来看一下二分法和牛顿法的比较
二分法和牛顿法的优缺点:
二分法:需要区间,结果比较可靠,但是比较慢
牛顿法:速度快,有时候不收敛,同时需要知道函数的微分
下面是最后一个单元 递归函数
recursive functions 递归函数
自己调用自己 functions that call themselves
举例:计算阶乘factorial

阶乘可以用另一个阶乘来表示(递推公式)
n!=n*(n-1)!
递归函数大家都学过,这里使用英文版的了解一下。
递归函数需要退出条件,基础情况;需要递推公式

下面给出一个计算阶乘的递归函数
function output =fact(n)
if n==1
output =1;
else
output=n*fact(n-1);
end
end
参考资料:
[1]B站av41338843视频
[2]matlab官方文档
【总结一下】
学习了求解非线性方程组的函数fsolve()的使用。
还有一个求根函数fzero(),适用条件:函数图像穿过x轴
还有针对多项式的求根公式roots()
后面介绍了两种求根的原理:二分法和牛顿法(切线逼近,速度快)
最后提及 递归函数recursive function