线段树入门(c++)(≧∇≦)ノ
线段树入门(代码方面采用C++)---出自南昌理工学院ACM集训队
- 线段树概念
- 线段树应用
- 图例
- 线段树各类操作
- 1.建树
- 2.修改特点区间的值
- 3.线段树经典操作(求和)
- 例题
- 懒标记
- 对比一下加了懒标记前后的测试点信息
- 最后附上例题AC代码
- 编程一路任重道远,加油吧陌生人( •̀ ω •́ )y
别问,问就是只会C++。。。
线段树概念
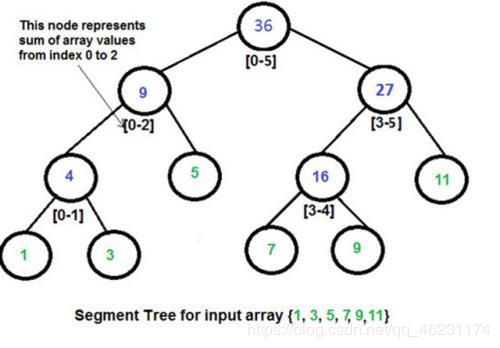
线段树是一种二叉搜索树,它将一个区间(编号1~n)划分成一些单元区间(arr),每个单元区间对应线段树中的一个叶结点;
对于线段树中的每一个结点都代表了一条线段,每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。对于叶子节点,a=b,叶子结点表示对应区间(arr)内的存储数据;
线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。线段树的优点在于,可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩;
线段树应用
线段树的原理是,通过对子区间的修改和统计来实现对大区间的修改(因此线段树需要用到递归的的知识)。因此线段树的运用需要符合区间加法原则。例如求数字之和、GCD与最大值。否则无法通过子区间统计,例如求众数;
总而言之,只要能化成对一些连续点的修改和统计问题,基本可以用线段树来解决;
友情提示:先学好递归吧
在此推荐一位B站UP主的线段树入门视频------->B站up主(正月点灯笼)
博主也是看着他的视频一步一步学习线段树;[]( ̄▽ ̄)*
图例
线段树的每一个结点都是一个区间,代表两子节点数值相加,在程序中选择用数组存储;
由此上树arr数组与tree(线段树)数组如下:
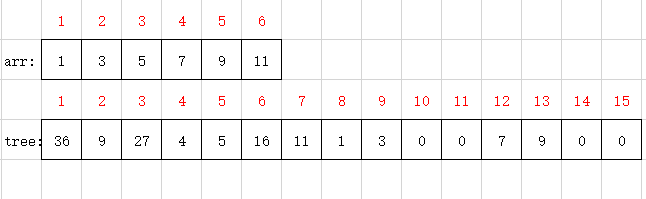
在此,可能就有小伙伴疑惑,数组开多大才够用?
对比上面两张图我们可以发现,树中一些不存在的点,在tree数组中我们用0来存;
因此上图tree数组的大小就是一颗高度为4的满二叉树的大小----->2^4-1
另外,根据dalao们的说法,arr长度为N时,tree开到4*N是完全够用的;
线段树各类操作
1.建树
ll arr[100005];
ll tree[400020];
void build_tree(int node,int start,int end){//初始值为0 1 n
if(start==end){//相等是即为叶子节点,将arr数组中end或start位置的值赋入即可
tree[node]=arr[end];
}
else{
int mid=(start+end)/2;//中点
int left_node=2*node;//左子树
int right_node=2*node+1;//右子树
build_tree(left_node,start,mid);//递归遍历左右子树
build_tree(right_node,mid+1,end);
tree[node]=tree[left_node]+tree[right_node];//父结点为左右两个子节点之和
}
}
2.修改特点区间的值
这里做的操作是将区间【L,R】内的值加上k
void update_tree(int node,int start,int end,int L,int R,ll k){
if(start==end&&end>=L&&end<=R){//start与end相等时将arr与tree数组内的值都加上k
arr[end]+=k;//递归的限定条件能够保证此时arr[end]必在[L,R]范围内,直接加上k
tree[node]+=k;
}
else{
int mid=(start+end)/2;
int left_node=2*node;
int right_node=2*node+1;
if(L<=mid) update_tree(left_node,start,mid,L,R,k);//遍历左右子树
if(R>mid) update_tree(right_node,mid+1,end,L,R,k);
tree[node]=tree[left_node]+tree[right_node];
}
}
上方代码块中,递归的条件(L<=mid时遍历左子树),(L>mid时遍历右子树)
对于每一次递归,L与R的值不变,因此用L与R的值与该次递归的mid值做比较,判断需要往哪个子树进行递归
3.线段树经典操作(求和)
long long add_tree(int node,int start,int end,int L,int R){
if(R<start||L>end){//表示所求区间L与R不在当前区间中,返回0
return 0;
}
else if(L<=start&&end<=R){//表示当前区间全部包含在[L,R]中返回区间结点值
return tree[node];
}
else if(start==end){
return tree[node];
}
else{
int mid=(start+end)/2;//这三行操作都见不少次了,主要是为了方便理解
int left_node=2*node;
int right_node=2*node+1;
int sum_left=add_tree(left_node,start,mid,L,R);//递归遍历
int sum_right=add_tree(right_node,mid+1,end,L,R);
return sum_left+sum_right;//因为函数返回值为long long ,返回值即为左右两子树之和
}
}
文字解释比较粗糙,如果难以理解的话,还请戳上方的视频链接,dalao的视频中也有关于这三种操作的详解;
例题
题出luoguP3372((模板题)线段树1)

看到这个题目,大家就会发现,题目中要求的操作与上方代码块中给出的各个操作相同(连返回值都是long long);
然后咱们开开心心拿着博文中代码块的函数去写题,然后开开心心地TLE(;´༎ຶД༎ຶ`)
博文上方给出的线段树各类操作都比较基础,而题目中的数据比较大,此时,就需要用到一个神奇的东西——>懒标记
懒标记
懒标记的优点就是:省时!省时!省时!
懒标记的精髓就是做标记和下传操作,由于我们要做的操作是区间相加,就在区间修改时若被覆盖,对当前结点做懒标记,当后续操作需要用到该结点的左右子结点时,将懒标记下传即可;
接下来看看具体操作:
首先存储方面采用结构体数组
typedef long long ll;
ll a[100005];
struct lq{
int l,r;//表示该节点的区间范围
ll num;//表示节点数据
ll add;//懒标记
}t[400010];
懒标记:
void spread(int node){
int l=node*2;
int r=node*2+1;
if(t[node].add){//当懒标记不为0的时候,将懒标记下传
t[l].num+=t[node].add*(t[l].r-t[l].l+1);//修改左右结点的值
t[r].num+=t[node].add*(t[r].r-t[r].l+1);
t[l].add+=t[node].add;//懒标记下传
t[r].add+=t[node].add;
t[node].add=0;//下传后该节点懒标记清零
}
建树:
void build_tree(int node,int start,int end){//和上面的建树差不多,只是加了一个结构体内l与r的赋值
t[node].l=start;
t[node].r=end;
if(start==end){
t[node].num=a[end];
return ;
}
int mid=(start+end)/2;
int left_node=node*2;
int right_node=node*2+1;
build_tree(left_node,start,mid);
build_tree(right_node,mid+1,end);
t[node].num=t[left_node].num+t[right_node].num;
}
修改区间值:
void update_tree(int node,int x,int y,int z){
if(x<=t[node].l && y>=t[node].r){//当区间覆盖时,即该函数区间[l,r]在[x,y]内
t[node].num+=(ll)z*(t[node].r-t[node].l+1);//该节点加(t[node].r-t[node].l+1)个z
t[node].add+=z;//对结点进行懒标记
return ;
}
spread(node);//否则,需要用到该节点的子节点,将懒标记下传
int left_node=node*2;//后面的就都一样了
int right_node=node*2+1;
int mid=(t[node].l+t[node].r)/2;
if(x<=mid) update_tree(left_node,x,y,z);
if(y>mid) update_tree(right_node,x,y,z);
t[node].num=t[left_node].num+t[right_node].num;
}
求区间和:
ll add_tree(int node,int x,int y){
if(x<=t[node].l && y>=t[node].r) {//同理,覆盖的时候直接返回该结点值,即该区间数值总和
return t[node].num;
}
spread(node);//否则,将懒标记下传
int mid=(t[node].l+t[node].r)/2;//接下来就都一样
int left_node=node*2;
int right_node=node*2+1;
ll sum=0;
if(x<=mid) sum+=add_tree(left_node,x,y);
if(y>mid) sum+=add_tree(right_node,x,y);
return sum;
}
对比一下加了懒标记前后的测试点信息
最后附上例题AC代码
#include