李宏毅老师课程Classification: Logistic Regression
逻辑回归
- Three Steps of Machine Learning
- Step 1: Function Set
- Step 2:Goodness of a Function
- Step 3:Find the Best Function
- Logistic Regression V.s. Linear Regression
- compare in step 1
- compare in step 2
- compare in step 3
- Discriminative v.s. Generative
- Multi-class Classification
- Limitation of Logistic Regression
- Feature Transformation
- Powerful Cascading Logistic Regression
Three Steps of Machine Learning
Step 1: Function Set
这⾥的function set就是Logistic Regression——逻辑回归
wi : weight , b :bias,σ(z) :sigmoid function, xi :input

Step 2:Goodness of a Function
现在我们有N笔Training data,每一笔data都要标注它是属于哪⼀个class
假设这些Training data是从我们定义的posterior Probability中产⽣的(后置概率,某种意义上就是概率密度函数),而w和b就决定了这个posterior Probability,那我们就可以去计算某⼀组w和b去产⽣这N笔Training data的概率,利⽤极大似然估计的思想,最好的那组参数就是有最大可能性产生当前N笔Training data分布的w和b

经过一系列运算,我们要找的参数实际上就是:
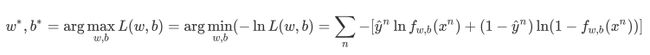
Step 3:Find the Best Function
实际上就是去找到使loss function最小的那组参数w*和b*就行了,这里用gradient descent的方法进行运算就ok
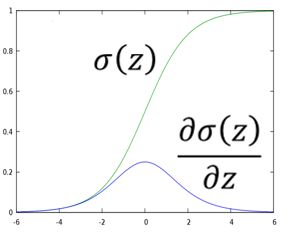
这里sigmoid function的微分可以直接作为公式记下来:
![]()
sigmoid和它的微分的图像如下:
整体推导过程如下:

将得到的式子进行进一步化简,可得:

最终式子代表现在你的update取决于三件事:
- η即learning rate,是你自己设定的
- xi,来自于data
- y - f ,代表function的output跟理想target的差距有多大,如果离目标越远,update的步伐就要越大
Logistic Regression V.s. Linear Regression
compare in step 1
Logistic Regression是把每⼀个feature 加权求和,加上bias,再通过sigmoid function,当做function的output
因为Logistic Regression的output是通过sigmoid function产⽣的,因此⼀定是介于0~1之间;而linear Regression的output并没有通过sigmoid function,所以它可以是任何值
compare in step 2
在Logistic Regression中,我们定义的loss function,即要去minimize的对象,是所有example(样本点)的output和实际target在Bernoulli distribution(两点分布)下的cross entropy(交叉熵) 总和
而在linear Regression中,loss function的定义相对比较简单,就是单纯的function的output和实际target在数值上的平方和的均值
compare in step 3
Logistic Regression和Linear Regression的update的方式是⼀模⼀样的,唯⼀不⼀样的是,Logistic Regression的target和output都必须是在0和1之间的,而linear Regression的target和output的范围可以是任意值
Discriminative v.s. Generative
判别模型 vs 生成模型
Logistic Regression的方法,我们把它称之为Discriminative的方法;而我们⽤Gaussian来描述posterior Probability这件事,我们称之为Generative的方法

它们⽤的model(function set)是⼀模⼀样的,如果是⽤Logistic Regression的话,可以⽤gradient descent的⽅法直接去把b和w找出来;如果是⽤Generative model的话,我们要先去算μ1,μ2,Σ ,然后算出b和w
你会发现⽤这两种方法得到的b和w是不同的,尽管我们的function set是同⼀个,但是由于做了不同的假设,最终从同样的Training data⾥找出来的参数会是不⼀样的
总之,Generative model和Discriminative model的差别就在于,Generative的model它有做了某 些假设,假设你的data来自于某个概率模型;而Discriminative的model是完全不作任何假设的
Generative model的好处是,它对data的依赖并没有像Discriminative model那么严重,在data数量少或者data本身就存在noise的情况下受到的影响会更小,而它还可以做到Prior部分与class-dependent部分分开处理,如果可以借助其他方式提高Prior model的准确率,对整⼀个model是有所帮助的(比如语音辨识)
而Discriminative model的好处是,在data充足的情况下,它训练出来的model的准确率⼀般是比Generative model要来的高的
Multi-class Classification
Limitation of Logistic Regression
Logistic Regression其实有很强的限制,给出下图的例子中的Training data,想要⽤Logistic Regression对它进行分类,其实是做不到的
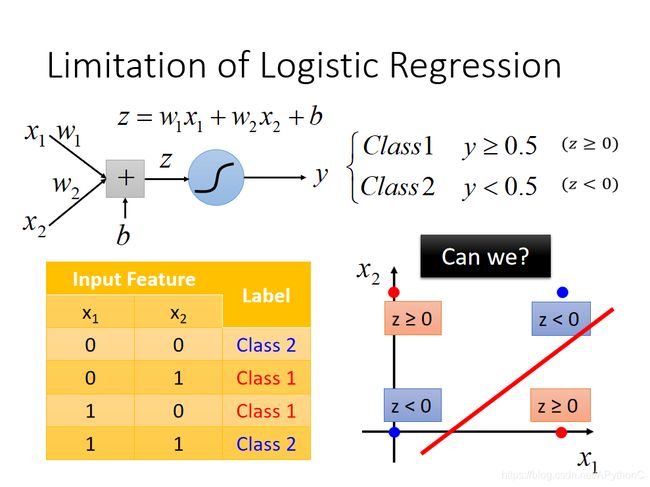
因为Logistic Regression在两个class之间的boundary就是⼀条直线,但是在这个平面上论怎么画直线都不可能把图中的两个class分隔开来
Feature Transformation
如果坚持要用Logistic Regression的话,有⼀招叫做Feature Transformation,原来的feature分布不好划分,那我们可以将之转化以后,找⼀个比较好的feature space,让Logistic Regression能够处理
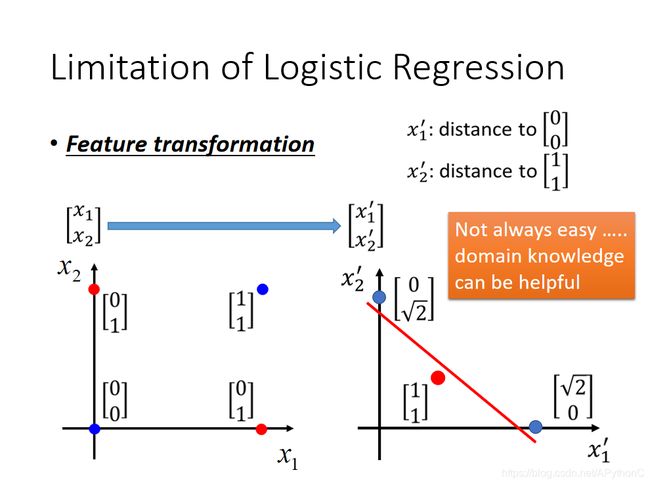
我们可以让很多Logistic Regression cascade(连接)起来,从而让机器自己产生这个transformation



这⾥的Logistic Regression只是⼀条直线,它指的是“属于这个类”或“不属于这个类”这两种情况, 因此最后的这个Logistic Regression是跟要检测的目标类相关的,当只是⼆元分类的时候,最后只需要⼀个Logistic Regression即可,当面对多元分类问题,需要用到多个Logistic Regression来画出多条直 线划分所有的类,每⼀个Logistic Regression对应它要检测的那个类
Powerful Cascading Logistic Regression
通过上面的例子,我们发现多个Logistic Regression连接起来会产⽣powerful的效果,我们把每⼀个Logistic Regression叫做⼀个neuron(神经元),把这些Logistic Regression串起来所形成的network,就叫做Neural Network,就是类神经网路,这个东西就是Deep Learning!

本文图片来自李宏毅老师课程PPT,文字是对李宏毅老师上课内容的笔记或者原话复述,在此感谢李宏毅老师的教导。


