使用简单的神经网络实现区分鸢尾花类别

原理

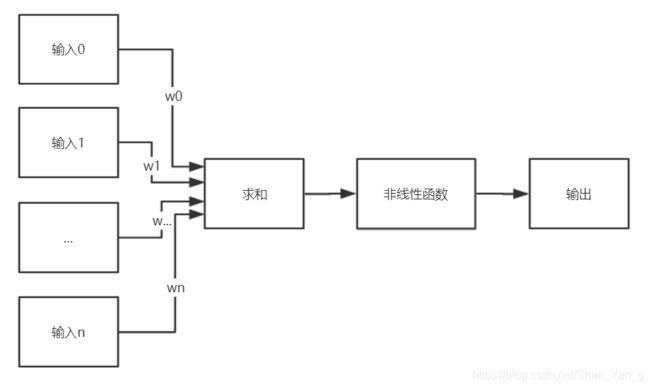
MP模型是Warren McCulloch(麦卡洛克)和Walter Pitts(皮茨)在1943年根据生物神经元的结构和工作原理提出的一个抽象和简化了的模型：

此次神经网络实现鸢尾花（Iris）分类省去了非线性函数（激活函数）的步骤，直接通过n个输入与权重的积再与偏置量求和得到输出y，即:

Y = x * w + b

那么x, 与y 如何得到呢？

通常人们根据生活经验，量取鸢尾花的花萼长、宽，花瓣长、宽，并且依据数据间的关系判断鸢尾花的类别。比如，花萼长>花萼宽且花瓣长为花瓣宽的两倍以上时为杂色鸢尾花（1）。(本文将鸢尾花分为三类，分别为狗尾草鸢尾（Setosa Iris，标签设定为0）、杂色鸢尾（Versicolour Iris， 标签设定为1）、弗吉尼亚鸢尾（Virginica Iris，标签设定为2）)

将这四个数据作为输入特征x，形状为（1，4），每个对应标签为y，形状为（1，3），在搭建网络时随机初始化所有参数w和b，w形状为（4，3），b形状为（3，），通过计算损失函数loss与准确率acc，判断是否寻找到w和b的最优参数。

代码实现

完成本次分类编程需要在Python环境下引入如下库：

import tensorflow as tf
import numpy as np
from sklearn import datasets
from matplotlib import pyplot as plt

准备数据阶段

首先完成这个分类任务需要采集大量辨别鸢尾花所需的数据（输入特征）以及对应的类别（标签），形成数据集，此处我们使用sklearn库中的datasets读入数据集： 

from sklearn.datasets import load_iris

返回数据集所有输入特征：

x_d = datasets.load_iris().data

返回iris数据集所有标签：

y_t = datasets.load_iris().target

至此导入了鸢尾花数据集并且将相应数据作为输入特征和对应标签。

将输入特征x与对应标签y数据一一对应地打乱顺序：

np.random.seed(1)           # 使用用一个种子 保持输入特征与标签对应
np.random.shuffle(x_d)
np.random.seed(1)
np.random.shuffle(y_t)
tf.random.set_seed(1)

区分数据集中的训练集与验证集且两者不相交：

x_train = x_d[:-30]          # 使用切片，使前120组数据作为训练集，后30组数据作为验证集
x_test = x_d[-30:]
y_train = y_t[:-30]
y_test = y_t[-30:]

将x_train, y_train转换为tensor浮点型32位：

x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

tf.cast(张量名， dtpye=数据类型)：强制tensor转换为该数据类型。

为了组成（输入特征，标签）的形式，每次喂入一个batch（此处设定32组数据为一个batch）：

train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

tf.data.Dataset.from_tensor_slices((输入特征，标签))：生成输入特征与标签对。

搭建神经网络阶段

现在定义神经网络中所有可训练参数，即使用MP模型，设定输入特征的权重（w）和偏置量（b）：

w = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

tf.Variable(初始值)：将变量标记为“可训练”，可训练变量在反向传播中记录梯度信息，

tf.random.truncated_normal(维度， mean=均值（默认为0），stddev=标准差（默认为1）)：生成截断式正态分布的随机数。

设置其他所需参数：

lr = 0.2                  # 此处设置学习率为0.2，学习率大小影响函数收敛快慢，过大过小都不好
train_loss_list = []      # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc_list = []        # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 250               # 此处设置循环250轮
loss_all = 0              # 初始化loss_all的值，用于记录每轮四个step生成的4个loss的和

超参数学习率设置过小时，收敛过程会十分缓慢，而学习率过大时，梯度可能会在最优值附近震荡但无法完成收敛。

更新参数，实现模型优化

loss损失函数使用均方误差MSE公式计算预测值与标准答案的差距，差距越小越好；

使用梯度下降法找到最优参数w和b，使得loss损失函数最小；

反向传播逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数（w，b）；

此处使用2层for循环嵌套循环迭代，使用with结构更新参数，并且显示此时的loss值：

for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:
            y = tf.matmul(x_train, w) + b
            y = tf.nn.softmax(y)                         # 使输出结果符合概率分布
            y_ = tf.one_hot(y_train, depth=3)            # 将标签转化为独热码格式
            loss = tf.reduce_mean(tf.square(y_ - y))     # 使用均方差损失函数mse计算损失函数
            loss_all += loss.numpy()
        grads = tape.gradient(loss, [w, b])              # 计算loss对各个参数的梯度
        w.assign_sub(lr * grads[0])                      # 更新模型权重参数w
        b.assign_sub(lr * grads[1])                      # 更新模型偏置量参数b
    print("Epoch: {}, loss: {}".format(epoch, loss_all/4))
    train_loss_list.append(loss_all / 4)                 # 记录loss_all均值放入列表
    loss_all = 0                                         # 归零，便于记录下一个epoch的loss

enumerate是python内建函数，遍历每个元素，enumerate（列表名），组合为：（索引，元素）；

独热码做标签，1表示是，0表示非，tf.one_hot(待转换数据，depth=几分类)；

tf.nn.softmax(x)使输出符合概率分布；

assign_sub(要自减的内容)；

因为总共有4个step（120/32向上取整），所以将求得的4个loss取平均值作为记录的loss。

初始化参数：

    total_correct, total_number = 0, 0

测试当前参数前向传播准确率，并且显示当前的准确率（acc）:

    for x_test, y_test in test_db:
        y = tf.matmul(x_test, w) + b    
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)                # 返回y中最大值的索引，即鸢尾花的分类标签
        pred = tf.cast(pred, dtype=y_test.dtype)   # 转换数据类型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32) # 根据分类是否正确返回布尔 
                                                                  # 值且转换为int型
        correct = tf.reduce_sum(correct)
        total_correct += int(correct)
        total_number += x_test.shape[0]
    acc = total_correct / total_number             # 总正确次数/总预测次数，计算准确率
    test_acc_list.append(acc)                      # 添加准确率数据到列表记录下来
    print("acc: ", acc)
    

tf.argmax(张量名，axis=操作轴)：返回操作轴上最大值的索引；

此代码包含在上一个代码第一层for循环中。

可视化处理acc/loss

使用Matplotlib库的pyplot绘制acc/loss

plt.title('Acc Curve')                                        # 图片标题
plt.xlabel('迭代次数', fontproperties='SimHei', fontsize=15)  # x轴变量名称
plt.ylabel('准确率', fontproperties='SimHei', fontsize=15)    # y轴变量名称
plt.plot(test_acc_list, label="$Accuracy$")                   # 逐点画出test_acc值并连线
plt.legend()                                                  # 画出曲线图标
plt.show()                                                    # 画出图像

plt.title('Loss Function Curve')                             
plt.xlabel('迭代次数', fontproperties='SimHei', fontsize=15)  
plt.ylabel('损失函数', fontproperties='SimHei', fontsize=15)  
plt.plot(train_loss_list, label="$Loss$")              # 逐点画出trian_loss_results值并连线
plt.legend() 
plt.show() 

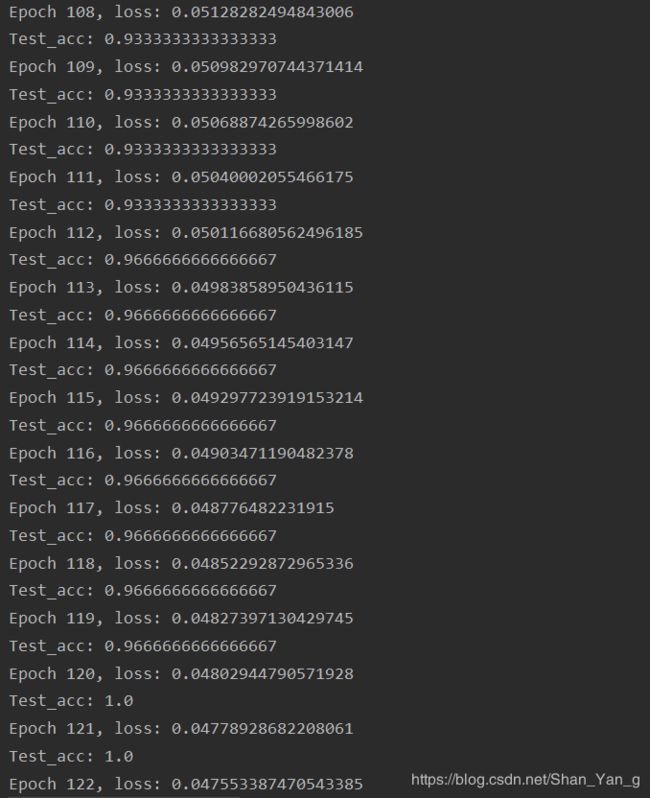
代码运行结果如下，可以看到迭代到第121轮时（epoch=120）准确率达到了1，loss值为0.048：

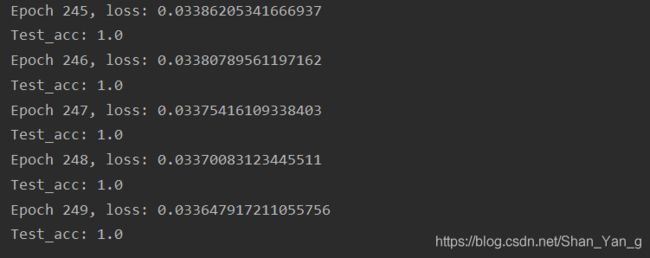
在设定的最后一次迭代完成后，准确率依然为1，loss下降到0.033：

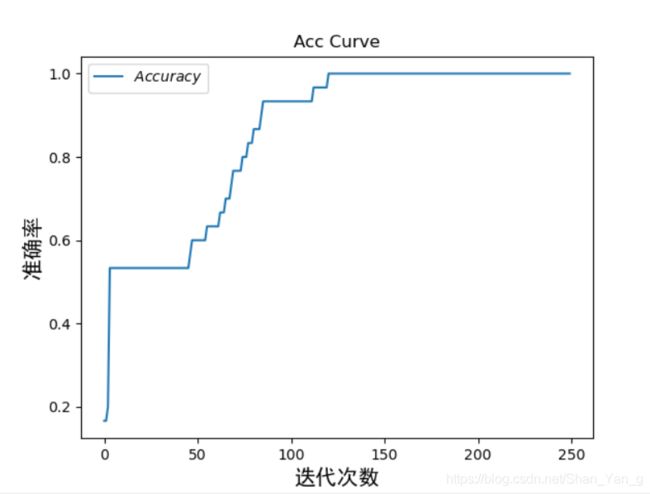
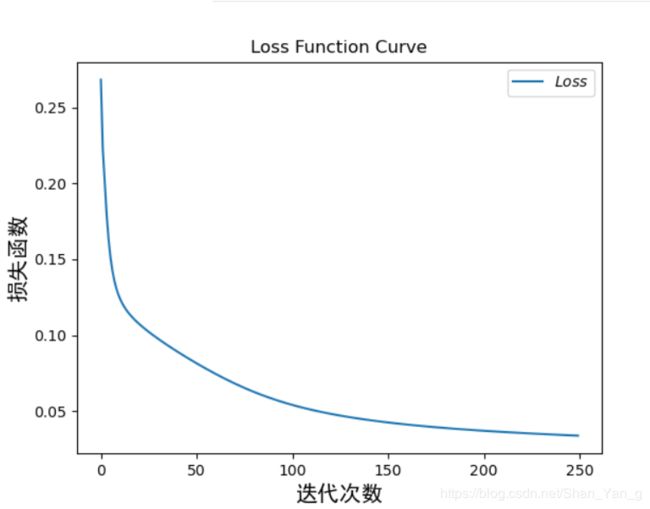
其Acc与Loss曲线可视化如下图所示：

我们可以修改学习率lr=0.1，看看准确率是否会更快到达1，loss是否能更接近0：

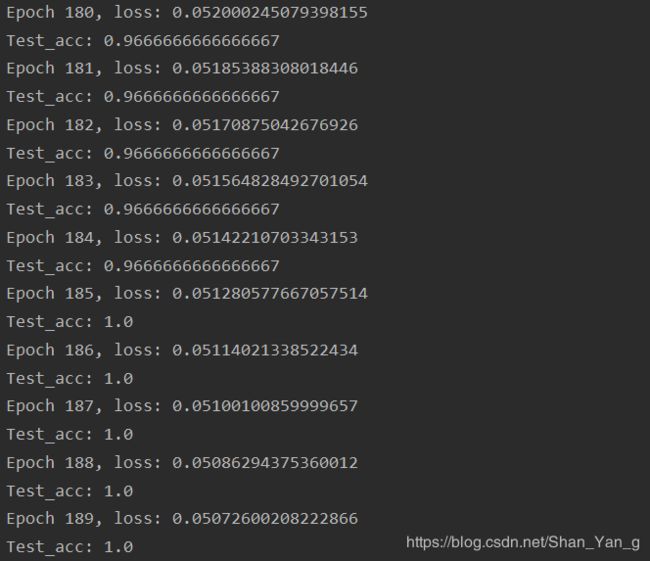
可以看到这次的运行结果在epoch=185时，Acc才达到1，并且loss=0.05；

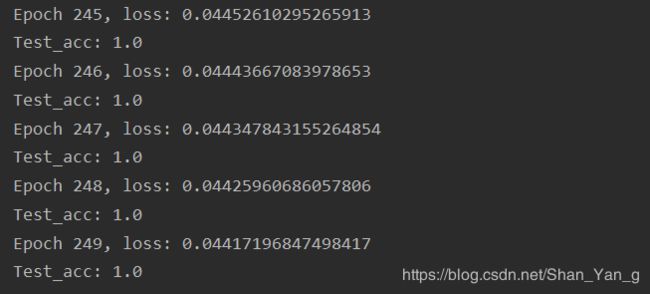
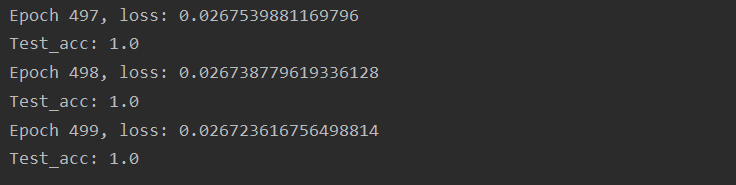
在最后一轮迭代完成后，虽然与之前lr=0.2代码的运行结果相比都能将Acc达到1，但是loss=0.044略微变大，我们再尝试保持lr=0.2，将epoch从250改为500，看结果是否会有变化：

因为lr=0.2，所以同样在epoch=120时acc达到1；

在最后一轮迭代完成后，loss略微下降为0.026；

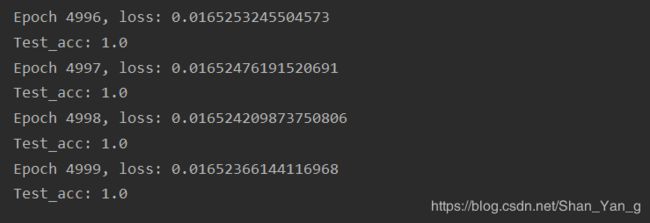
当设置epoch=5000时，运行结束后loss下降为0.016：

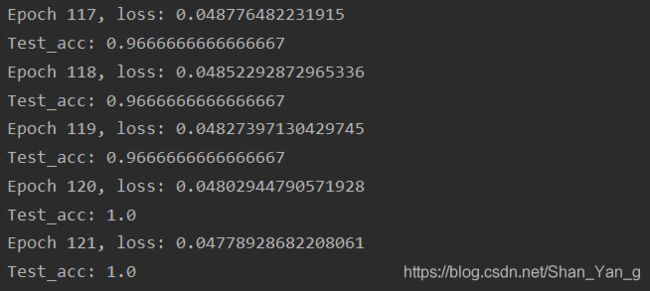
设置lr=0.25时，acc在epoch=117时达到1，设置lr=0.3时，acc在epoch=119时达到1，可见学习率可以通过试探逐渐找到收敛最快的值，loss值可以通过增加训练迭代次数来降低。