HDU 1992 Tiling a Grid With Dominoes（轮廓线dp || 插头dp 简讲）

Problem Description
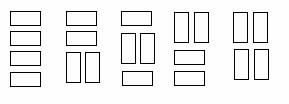
We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.

Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-W grid.

Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.

Output
For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.

题意大概就是有一个n*4的网格，现在有一堆1x2的骨牌，问要将网格全部铺满有多少种方法。

这就是轮廓线dp的裸题。

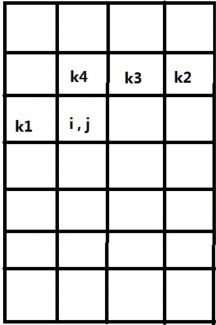
轮廓线dp其实就是一种将边界的轮廓也列入dp状态的一种装压dp，，用本题来举例，假设所有骨牌都是朝左放或朝上放（相当于我们总是将骨牌的右下角放在当前格子），如果我们当前决策的格子为（i，j），那么这个格子的骨牌有三种情况，不放，朝左放，或朝上放。我们用二进制来表示当前的轮廓线即有骨牌的格子为1，没有骨牌的格子为0；

则此时的轮廓线即状态为k1 k2 k3 k4；
如果k4为0的话，那么当前格子的骨牌可以向上放，但是不能向左放（因为如果当前骨牌向左放，，那么上面的格子仍然是空的，而且不会有其他格子的骨牌能填上k4，而题意要求所有格子都要填满），那么就能转移到状态k1 k2 k3 1；
如果k4不为0且k1不为0，那么就可以向左放，状态为1 k2 k3 1；
如果k4不为0，那么当前格子也可以选则不放，那么状态就是 k1 k2 k3 k4；
当我们转移到下一个格子时，注意要将表示状态的二进制左移一位，因为我们当前的k都是相对于当前格子的，如果对于下一个格子，那么k应顺次移一位，而且在位移的时候，注意要改变当前格子的状态。
还有就是我们的位运算在左移时最高位有可能超出我们的dp范围，所以要将高位除去，可以令k&M，M是状态的最大值，这样最后输出答案就行了。
还可以用滚动数组优化一下。
代码如下：

#include
#include
#define M ((1<
using namespace std;
unsigned int n,m,f[2][1<<5],cur=0;
void dp(int i,int j) {
    for(int k=0;k<=M;k++) {
      if(!(k&(1<1))&&i>1) f[cur][((k<<1)^1)&M]+=f[cur^1][k];
      else if(!(k&1)&&j>1) f[cur][((k<<1)^1^2)&M]+=f[cur^1][k];
      if(i==1||(k&(1<1))) f[cur][(k<<1)&M]+=f[cur^1][k];
    }
}
int main() {
    int t;scanf("%d",&t);int a=0;
    while(t--) {
      scanf("%d",&n);m=4;
      memset(f,0,sizeof(f));
      f[cur^1][M]=1;
      for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++,cur^=1) {
          memset(f[cur],0,sizeof(f[cur]));
          dp(i,j); 
        }
      }
      printf("%d %d\n",++a,f[cur^1][M]);
    }
}