常见激活函数及其求导相关知识
文章目录
- Sigmoid函数
- Sigmoid函数介绍
- Sigmoid函数求导
- tanh 函数
- tanh 函数介绍
- tanh 函数求导
- Relu函数
- Relu函数介绍
- Relu函数求导
- Softmax函数
- Softmax函数介绍
- Softmax函数求导
- 激活函数作用
- 激活函数的选择
- 均值不为零问题
Sigmoid函数
Sigmoid函数介绍
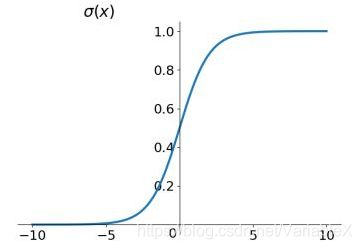
Sigmoid 是常用的非线性的激活函数,公式如下:
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
函数图像如下:
从图像可以看出,它能够把连续实值映射为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1。
Sigmoid 函数有很多局限性:
第一点,在数值的绝对值非常大的情况下,对应的函数图像的部分几乎是一条水平线。这意味着梯度几乎为0,不利于深层网络中梯度的反向传播,容易造成梯度消失。
第二点,Sigmoid 的输出不是0均值,导致梯度的更新要么都往正方向更新,要么都往负方向更新,导致有一种捆绑的效果,使得收敛缓慢。具体的解释,在文末讨论。
第三点,式子包含幂运算,计算量很大。
Sigmoid函数求导
求导过程及结果如下:
σ ′ ( x ) = ( 1 1 + e − x ) ′ = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 ( 1 + e − x ) 2 = σ ( x ) ( 1 − σ ( x ) ) \begin{aligned} \sigma^{\prime}(x) &=\left(\frac{1}{1+e^{-x}}\right)^{\prime} \\ &=\frac{e^{-x}}{\left(1+e^{-x}\right)^{2}} \\ &=\frac{1+e^{-x}-1}{\left(1+e^{-x}\right)^{2}} \\ &=\sigma(x)(1-\sigma(x)) \end{aligned} σ′(x)=(1+e−x1)′=(1+e−x)2e−x=(1+e−x)21+e−x−1=σ(x)(1−σ(x))
函数图像如下:
求导的结果可以看出,导数的最大值为0.25,小于1 ,很容易造成梯度消失。
tanh 函数
tanh 函数介绍
tanh 函数公式如下:
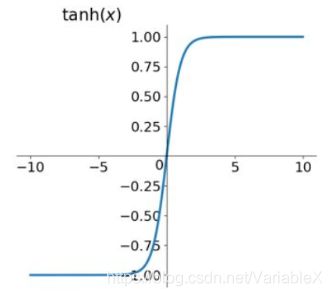
tanh ( x ) = e x − e − x e x + e − x \tanh (x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} tanh(x)=ex+e−xex−e−x
图像如下:
tanh 函数决了Sigmoid函数的输出不是0均值,然而,梯度消失和幂运算的问题仍然存在。
tanh 函数求导
求导过程如下:
t a n h ( x ) ′ = ( e x + e − x ) 2 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( t a n h ( x ) ) 2 tanh(x)^{\prime}=\frac{(e^{x}+e^{-x})^{2}-(e^{x}-e^{-x})^{2}}{(e^{x}+e^{-x})^{2}}=1-(tanh(x))^{2} tanh(x)′=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(tanh(x))2
求导后的图像:
Relu函数
Relu函数介绍
Relu函数公式如下:
R e L U ( x ) = { 0 , x ⩽ 0 x , x > 0 ReLU(x)=\begin{cases}{0,} & {x \leqslant 0} \\ {x,} & {x>0}\end{cases} ReLU(x)={0,x,x⩽0x>0
函数图像如下:
Relu 函数在输出值大于 0 的部分的导数值都大于0,并且不趋近于0,因而梯度下降速度较快。
Relu 函数在输出值小于 0 的部分的导数值都等于0,此时神经元就不会得到训练,能对网络产生稀疏性,降低过分拟合的概率。
但是也存在以下问题:
- 输出不是0均值
- Dead ReLU Problem:因梯度等于0导致失效的神经元不会再被激活
注:为了解决第二个问题,有人提出了Leaky ReLU激活函数: L e a k y R e L U ( x ) = m a x ( 0.01 x , x ) Leaky \; ReLU(x) = max(0.01x, x) LeakyReLU(x)=max(0.01x,x),使得小于0的部分有些许梯度。
尽管ReLU存在这两个问题,ReLU目前仍是最常用的激活函数,在搭建模型的时候推荐优先尝试。
Relu函数求导
求导结果如下:
R e L U ( x ) ′ = { 0 , x ⩽ 0 1 , x > 0 ReLU(x)^{\prime}=\begin{cases}{0,} & {x \leqslant 0} \\ {1,} & {x>0}\end{cases} ReLU(x)′={0,1,x⩽0x>0
函数图像如下:
Softmax函数
Softmax函数介绍
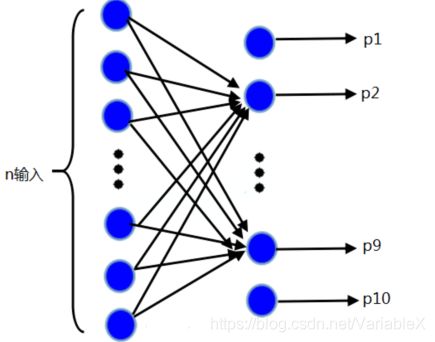
对于多分类任务,常用的激活函数是 Softmax 激活函数。使用了Softmax函数的神经网络对应多个输出层神经元 ,如下图所示;
每个输出单元的数值代表该类别的概率 p i p_i pi,数值越大,说明属于该类别可能性越大。
具体而言,假设倒数第二层的输出值为:
z i = w i x + b i z_i = w_i x + b_i zi=wix+bi
假设有K个类别,Softmax函数定义如下:
S o f t m a x ( z i ) = e z i ∑ i = 1 K e z i ∀ i ∈ 1 … K Softmax(z_i)=\frac{e^{z_i}}{\sum_{i=1}^{K} e^{z_i}} \quad \forall i \in 1 \ldots K Softmax(zi)=∑i=1Keziezi∀i∈1…K
则在最后一层使用 Softmax 激活函数后的输出值为:
h w ( x ) = [ p 1 p 2 ⋮ p K ] = 1 ∑ i = 1 K e z i [ e z 1 e z 2 ⋮ e z K ] h_w(x) = \begin{bmatrix}p_1\\p_2 \\ \vdots \\p_{K} \end{bmatrix} = \frac{1}{\sum_{i=1}^K e^{z_i}} \begin{bmatrix}e^{z_1}\\e^{z_2 } \\ \vdots \\e^{z_K} \end{bmatrix} hw(x)=⎣⎢⎢⎢⎡p1p2⋮pK⎦⎥⎥⎥⎤=∑i=1Kezi1⎣⎢⎢⎢⎡ez1ez2⋮ezK⎦⎥⎥⎥⎤
上式结果向量中最大值得对应类别为预测类别。
Softmax函数求导
Softmax 的损失函数是预测概率的负对数似然函数:
L ( w ) = − log P ( y ( i ) ∣ x ( i ) ; w ) = − ∏ k = 1 K log ( e z i ∑ j = 1 K e z j ) y k = − ∑ k = 1 K y k log ( e z k ∑ j = 1 K e z j ) \begin{aligned} L(w) &= - \log P(y^{(i)}|x^{(i)};w) \\ &= -\prod_{k=1}^{K} \log\left(\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \right)^{y_k} \\&=-\sum_{k=1}^K y_k \log\left(\frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}} \right) \end{aligned} L(w)=−logP(y(i)∣x(i);w)=−k=1∏Klog(∑j=1Kezjezi)yk=−k=1∑Kyklog(∑j=1Kezjezk)
注: y k = I { y ( j ) = k } y_k = I\{y^{(j)} = k\} yk=I{y(j)=k} 是指示函数,当 y ( j ) = k y^{(j)} = k y(j)=k,即当第 j j j个样本属于第 k k k个类别时,取值为1,否则为0。 我们的目标是:
min L ( w ) \min L(w) minL(w)
通过梯度下降法则求解最优参数。
设第 i i i 个输出为:
s i = e z i ∑ i = 1 K e z i i = 1 , 2 , … , K s_{i} = \frac{e^{z_i}}{\sum_{i=1}^K e^{z_i}} \quad i=1,2,\ldots,K si=∑i=1Keziezii=1,2,…,K
针对某一个样本:
∂ L ∂ w i = ∂ L ∂ z i ∂ z i ∂ w i ∂ L ∂ b i = ∂ L ∂ z i ∂ z i ∂ b i \begin{aligned} \frac{\partial L}{\partial w_i} &= \frac{\partial L}{\partial z_i} \frac{\partial z_i}{\partial w_i} \\ \frac{\partial L}{\partial b_i} &= \frac{\partial L}{\partial z_i} \frac{\partial z_i}{\partial b_i} \end{aligned} ∂wi∂L∂bi∂L=∂zi∂L∂wi∂zi=∂zi∂L∂bi∂zi
显然:
∂ z i ∂ w i = x ∂ z i ∂ b i = 1 \frac{\partial z_i}{\partial w_i} = x \\ \frac{\partial z_i}{\partial b_i} = 1 ∂wi∂zi=x∂bi∂zi=1
所以核心问题是求 ∂ L ∂ z i \frac{\partial L}{\partial z_i} ∂zi∂L:
∂ L ∂ z i = ∑ k = 1 K [ ∂ L ∂ s k ∂ s k ∂ z i ] \frac{\partial L}{\partial z_i} = \sum_{k=1}^K \left[ \frac{\partial L}{\partial s_k} \frac{\partial s_k}{\partial z_i} \right] ∂zi∂L=k=1∑K[∂sk∂L∂zi∂sk]
其中 ∂ L ∂ s k \frac{\partial L}{\partial s_k} ∂sk∂L为:
∂ L ∂ s k = ∂ ( − ∑ k = 1 K y k log s k ) ∂ s k = − y k s k \frac{\partial L}{\partial s_k} = \frac{\partial \left(-\sum_{k=1}^K y_k \log s_k \right)}{\partial s_k} = - \frac{y_k}{s_k} ∂sk∂L=∂sk∂(−∑k=1Kyklogsk)=−skyk
接下来就是要求 ∂ s k ∂ z i \frac{\partial s_k}{\partial z_i} ∂zi∂sk 了。先来复习一下复合求导公式:
f ( x ) = g ( x ) h ( x ) f ′ ( x ) = g ′ ( x ) h ( x ) − g ( x ) h ′ ( x ) [ h ( x ) ] 2 f(x) = \frac{g(x)}{h(x)} \\ f'(x) = \frac{g'(x) h(x) - g(x)h'(x)}{[h(x)]^2} f(x)=h(x)g(x)f′(x)=[h(x)]2g′(x)h(x)−g(x)h′(x)
根据 k 与 i 的关系,需要分两种情况讨论:
(1)当 k ≠ i k \ne i k=i时,那么:
∂ s k ∂ z i = ∂ e z k ∑ j = 1 K e z j ∂ z i = − e z k ⋅ e z i ( ∑ j = 1 K e z j ) 2 = − e z k ∑ j = 1 K e z j e z i ∑ j = 1 K e z j = − s k s i \begin{aligned} \frac{\partial s_k}{\partial z_i} &= \frac{\partial \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}} }{\partial z_i} \\ &= \frac{-e^{z_k}\cdot e^{z_i}}{(\sum_{j=1}^K e^{z_j})^2} \\ &=-\frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}} \frac{ e^{z_i}} {\sum_{j=1}^K e^{z_j}} \\ &= -s_k s_i \end{aligned} ∂zi∂sk=∂zi∂∑j=1Kezjezk=(∑j=1Kezj)2−ezk⋅ezi=−∑j=1Kezjezk∑j=1Kezjezi=−sksi
(2)当 k = i k = i k=i时,那么:
∂ s k ∂ z i = ∂ s i ∂ z i = ∂ e z i ∑ j = 1 K e z j ∂ z i = e z i ∑ j = 1 K e z j − ( e z i ) 2 ( ∑ j = 1 K e z j ) 2 = e z i ∑ j = 1 K e z j ∑ j = 1 K e z j − e z i ∑ j = 1 K e z j = s i ( 1 − s i ) \begin{aligned} \frac{\partial s_k}{\partial z_i} &= \frac{\partial s_i}{\partial z_i} =\frac{\partial \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} }{\partial z_i} \\ &= \frac{e^{z_i}\sum_{j=1}^K e^{z_j} - (e^{z_i})^2}{(\sum_{j=1}^K e^{z_j})^2} \\ &=\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \frac{\sum_{j=1}^K e^{z_j} - e^{z_i}} {\sum_{j=1}^K e^{z_j}} \\ &= s_i(1-s_i) \end{aligned} ∂zi∂sk=∂zi∂si=∂zi∂∑j=1Kezjezi=(∑j=1Kezj)2ezi∑j=1Kezj−(ezi)2=∑j=1Kezjezi∑j=1Kezj∑j=1Kezj−ezi=si(1−si)
所以:
∂ L ∂ z i = ∑ k = 1 K [ ∂ L ∂ s k ∂ s k ∂ z i ] = ∑ k = 1 K [ − y k s k ∂ s k ∂ z i ] = − y i s i ∂ s i ∂ z i + ∑ k = 1 , k ≠ i K [ − y k s k ∂ s k ∂ z i ] = − y i s i s i ( 1 − s i ) + ∑ k = 1 , k ≠ i K [ − y k s k ⋅ − s k s l ] = y i ( s i − 1 ) + ∑ k = 1 , k ≠ i K y k s i = − y i + y i s i + ∑ k = 1 , k ≠ i K y k s i = − y i + s i ∑ k = 1 K y k \begin{array}{l} \frac{\partial \mathrm{L}}{\partial \mathrm{z}_{i}}=\sum_{k=1}^{K}\left[\frac{\partial L}{\partial s_{k}} \frac{\partial s_{k}}{\partial z_{i}}\right]=\sum_{k=1}^{K}\left[-\frac{y_{k}}{s_{k}} \frac{\partial s_{k}}{\partial z_{i}}\right] \\ =-\frac{y_{i}}{s_{i}} \frac{\partial s_{i}}{\partial z_{i}}+\sum_{k=1, k \neq i}^{K}\left[-\frac{y_{k}}{s_{k}} \frac{\partial s_{k}}{\partial z_{i}}\right] \\ =-\frac{y_{i}}{s_{i}} s_{i}\left(1-s_{i}\right)+\sum_{k=1, k \neq i}^{K}\left[-\frac{y_{k}}{s_{k}} \cdot-s_{k} s_{l}\right] \\ =y_{i}\left(s_{i}-1\right)+\sum_{k=1, k \neq i}^{K} y_{k} s_{i} \\ =-y_{i}+y_{i} s_{i}+\sum_{k=1, k \neq i}^{K} y_{k} s_{i} \\ =-y_{i}+s_{i} \sum_{k=1}^{K} y_{k} \end{array} ∂zi∂L=∑k=1K[∂sk∂L∂zi∂sk]=∑k=1K[−skyk∂zi∂sk]=−siyi∂zi∂si+∑k=1,k=iK[−skyk∂zi∂sk]=−siyisi(1−si)+∑k=1,k=iK[−skyk⋅−sksl]=yi(si−1)+∑k=1,k=iKyksi=−yi+yisi+∑k=1,k=iKyksi=−yi+si∑k=1Kyk
对于某个样本 x x x对应的标签 y y y为一个向量: y = ( y 1 , y 2 , … , y K ) y=(y_1,y_2,\ldots,y_K) y=(y1,y2,…,yK),其中只有一个元素是1,如 y = ( 1 , 0 , … , 0 ) y=(1,0,\ldots,0) y=(1,0,…,0) 。所以有: ∑ k = 1 K y k = 1 \sum_{k=1}^{K} y_{k} = 1 ∑k=1Kyk=1,所以:
∂ L ∂ z i = s i − y i \frac{\partial \mathrm{L}}{\partial \mathrm{z}_{i}}= s_i - y_i ∂zi∂L=si−yi
所以最终结果为:
∂ L ∂ w i = ( s i − y i ) x ∂ L ∂ b i = s i − y i \frac{\partial L}{\partial w_i} = (s_i - y_i)x \\ \frac{\partial L}{\partial b_i} = s_i - y_i ∂wi∂L=(si−yi)x∂bi∂L=si−yi
所以,更新法则如下:
w i = w i − η ( s i − y i ) x b i = b i − η ( s i − y i ) w_i = w_i - \eta (s_i - y_i)x \\ b_i = b_i - \eta (s_i - y_i) \\ wi=wi−η(si−yi)xbi=bi−η(si−yi)
直至收敛为之。
激活函数作用
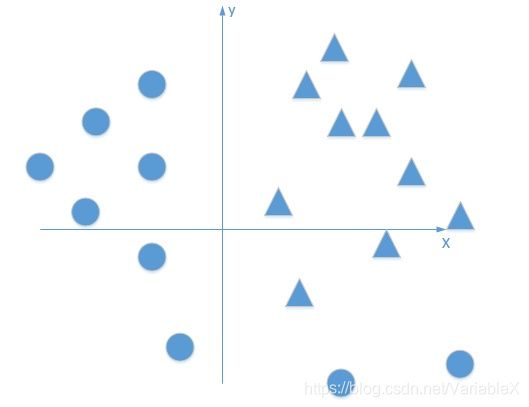
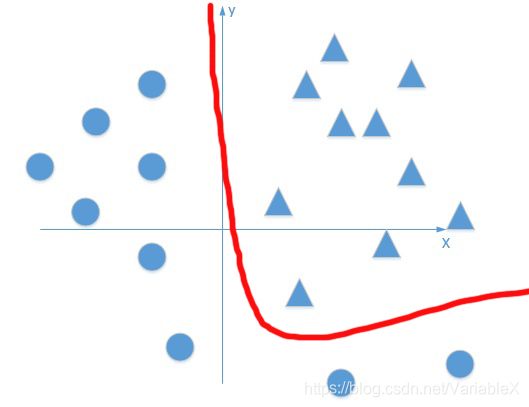
先看个例子,比如我们需要给下面的图像进行二分类,也就是找出圆圈和三角形的边界:
如果没有激活函数,我们训练出来的分类器是线性的,它的效果也许会是这样:
始终无法完美的完成任务。训练出来的模型只是把输入的数据线性组合后再输出,即使你有多个隐藏层,本质上也是在进行线性计算,其结果仍然是一个线性函数,无法完成复杂的分类任务。
然而,如果我们训练出来的模型是非线性的,那么它的分类效果可能是这样的:
要实现这样的分类效果,就需要借助非线性的激活函数(比如 tanh函数)将每一层的输出 z 进行一次非线性的变换。这样可以加入非线性因素,让原本的直线(或者平面)“扭曲”起来,达到拟合复杂的曲线(或者曲面)的效果,这样就提高神经网络对模型的表达能力,让神经网络的模型任意逼近复杂的函数。显然非线性拟合的效果要比线性拟合的效果好的多。
激活函数的选择
- sigmoid 激活函数:除了输出层是一个二分类问题基本很少用它。
- tanh 激活函数: tanh 是非常优秀的, 几乎适合所有场合。
- ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者Leaky ReLu。
均值不为零问题
假设输入与输出的关系为:
f ( x ⃗ ; w ⃗ , b ) = f ( z ) = f ( ∑ i w i x i + b ) . f(\vec x; \vec w, b) = f(z) = f\Bigl(\sum_iw_ix_i + b\Bigr). f(x;w,b)=f(z)=f(i∑wixi+b).
其中 f f f是激活函数。进而计算 w i w_i wi的梯度,于是有:
∂ L ∂ w i = ∂ L ∂ f ∂ f ∂ z ∂ z ∂ w i = x i ⋅ ∂ L ∂ f ∂ f ∂ z . \frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}\frac{\partial z}{\partial w_i} = x_i \cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}. ∂wi∂L=∂f∂L∂z∂f∂wi∂z=xi⋅∂f∂L∂z∂f.
发现梯度值包含 ∂ L ∂ f ∂ f ∂ z \frac{\partial L}{\partial f}\frac{\partial f}{\partial z} ∂f∂L∂z∂f,如果我们使用的激活函数是Sigmoid函数,那么 ∂ L ∂ f ∂ f ∂ z \frac{\partial L}{\partial f}\frac{\partial f}{\partial z} ∂f∂L∂z∂f这一项永远是正数,于是梯度的更新方向永远都被输入值 x i x_i xi的正负号决定了,每次迭代都只能向着固定的方向进行梯度下降,不利于收敛,也就降低了训练的速度。
参考文章:
-
深度学习中的激活函数介绍
-
softmax回归详解
-
谈谈激活函数以零为中心的问题