[latexpage]
话说当年学习导数和微分的时候,我也是一头雾水。当时我的感觉就是都有导数了,干嘛还要微分??而且微分看起来和导数长的那么像,咋看都像是导数的重复。最让我迷惑的是dx这个玩意,一会可以用来约分,一会又可以当做0,那么这两个不是矛盾的吗??比如下面一个例子:
今天终于有时间来好好弄明白这个问题了。有人建议说要搞懂这个问题要从微积分的发展史来看,确实是这样,不过我不建议上来就看这个历史,我会放在第二部分来讲。因为上来就看历史,先入为主,会造成更加的混乱。
下面的内容都是本人学习后根据自己所理解而写的,如有错误欢迎大神指正。
一、微分的本质
我直接先下个结论:微分本质是一个微小的线性变化量,是用一个线性函数作为原函数变化的逼近(或者叫近似)。
微分的定义是从导数而来的,我们简单回顾一下。
由导数的定义有$\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = f'(x)$,那么则有$\frac{{\Delta y}}{{\Delta x}} - f'(x) = a{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{\Delta {\rm{x}} \to 0} a = 0$。
则可以得到如下结果:
\[\Delta y = f'(x)\Delta x + a\Delta x\]
当$\Delta x$趋近于0,显然有$\Delta y \approx f'(x)\Delta x$。
现在我们将$f'(x)\Delta x$定义为dy。而$\Delta y$表示的是函数值的变化,显然dy的真正含义是对这种变化的逼近。也就是说我们定义微分,就是想借助微分这个工具来研究函数的变化趋势。
从上面你可以明白两件事,第一微分,即dy不是一个符号哦,是真的有具体值的,它的值为$f'(x)\Delta x$,第二观察下$f'(x)\Delta x$,显然是一个关于$\Delta x$的线性函数,因此微分其实在一点处,用一个线性函数的变化来逼近函数的变化,你懂的,线性的东西,其规律好掌握嘛。好了,这下你明白微分到底是什么含义了吧。
那么我们根据$dy = f'(x)\Delta x$还可以推导出更多东西,比如令里面的y为x,则可以得到$dx = 1*\Delta x$,即$dx = \Delta x$。那么x的微分也就出来了。说白了,dy和dx表示的就是y和x的变化量,是一种具体的量,跟我们通常理解的变化差额没什么本质区别,只不过因为$\Delta x$趋近0这种极限的性质,让他变得特殊一点而已。因此我们在数学上给他起个牛逼的代号,微分!以后用到微分的地方太多了,所以要起名字。
好,那么根据我们的定义,导数和微分的关系自然而然就出来了,由$dy = f'(x)dx$,自然就得到$\frac{{dy}}{{dx}} = f'(x)$。是不是觉得导数和微分的关系其实也没有那么神秘,这一切都只源于那些数学大家的定义而已。所谓定义,肯定是人为的了,没什么道理可讲。
从上面微分的提出过程我们可以到,是沿着极限、导数、微分这个次序来架构的。因此可以说极限是导数和微分的基石。然而在历史上,可不是这样子的,甚至因此而引发了第一次数学危机呢!
这就得联系到开头我提到的那个例子,它的做法到底是对的还是错的呢?好像大多数同学都喜欢这么做。其实是按照目前的微积分体系来看,是错误的。为什么呢?这就要从微分的发展历史来说了。
二、微分的发展历史
我们现在所学的微分学一定是按照先极限、后导数、再微分这个顺序来学。但历史的发展可不讲究顺序性。
其实一开始还没有极限还没有被发明的时候,人们因为实际需要,就迫切的发明出了微分。这段历史中的微积分学称之为古典微积分,古典微积分中产生了无穷小量这个概念,直接导致了第一次数学危机的产生。后来直到200多年后极限被发明出来,基于极限体系的微积分才完美解决了这个问题,数学家们开始基于极限思想将导数和微分的概念都重新建立了一遍。因此我们今天学习的都是极限微积分。但是有意思的是,在教材的介绍中,却总使用古典微积分的思想来使学生加强理解,最后的结果就是导致学生在学起来总觉得有糊里糊涂。而且不能真正的体味极限思想的本质含义。
2.1 古典微分
先给大家做个简单的介绍。
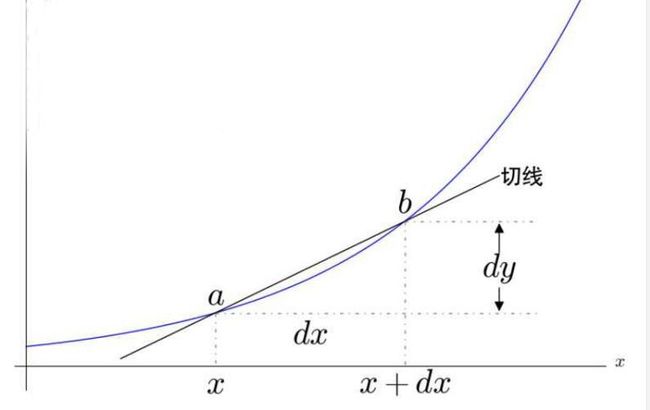
出于对函数变化趋势的研究需要,数学家们迫切想要知道函数在某一点处的变化值是多少。如下图:
于是数学家将函数值得变化量直接定义为dy,而将自变量x的变化量直接定义为dx。那么只要dx足够小,也就是说b点足够趋近于a,函数的割线就足够能够描绘出函数在这个邻域中的变化情况。
但是这还不够,数学家还想定义切线。当时给出的定义是dx无限小,则割线就会无限与其切线重合。那么小到一定程度(b与a重合),则割线自然就成为了切线。难道不是吗?
可是这个定义漏洞百出。因为我们都知道两点才能确定一条直线,如果b点都与a点重合了,那怎么会把切线给确定出来呢?数学家解释说,不重合,只是无限小。那么问题又来了,不管多小,只要不重合,那dx总会表示一段距离,那割线总会与函数有两个交点,有两个交点又怎么称之为切线呢?你看一个切线的定义真的是让数学家无所适从。其实本质是,dx作为一个无穷小量,让数学家手足无措。无穷小到底是个什么鬼??奈何当时极限还没有被发明,死活谁也说不清趋近于无穷小的dx是个什么鬼。
但是微小的变化量还是迫切需要的,因此数学家赶鸭子上架。强迫定义dy为y的微分,dx为x的微分(微分即微小的变化量)。因此微分这个词语在哪个时候已经被提出来了。然后把dy/dx定义为导数,也就是切线的斜率(即因变量微分与自变量微分之比为导数)。因此导数在那个时候又叫做微分的商。虽然定义了导数来表示斜率,通过点斜式解决了切线的求法。但是上面表述的关于切线的问题本质上并没有得到解决。
再自然而然的在计算导数时,就采取了这种方式(比如求x平方的导数):
也自然而然的产生了上图中我红色文字说明的问题。这问题就大了。有人开始抨击,尤其是教会的那些人,质问道dx到底是什么,一会为0,一会又不为0??为什么一个量会有两种不同形态,而且还能完全没道理的自由转换??于是第一次数学危机就这样爆发了。无穷小量直接挑战了数学的严谨性!没有严谨性的数学,将什么都不是!而在当时没有一个人将无穷小量说的清楚。
总结一下,古典微分学的特点:
(1)dy和dx表示的是自变量和因变量的具体的变化。
(2)根据想象中的无穷小这个东西,定义了切线。
(3)然后将切线的斜率定义为导数。
可以看到古典微分学确实很直观,如果不假思索,确实非常易于理解。这也是为什么我们在教材中,在介绍什么是导数,什么是切线时,还是采用上面那张图来介绍。但是古典微分学的缺陷是非常严重的,就是无穷小量像个炸弹一样,随时把这个体系炸的血肉模糊。如果我们能很好的解决无穷小量这个问题,那么一切危机不都消除了吗?遗憾的直到200年后,极限被数学家发明了出来,无穷小才得到完美的解决。
2.2 极限微分学
终于极限被发明了出来。相应的什么是无穷小,也有了确切的、具体的定义。无穷小终于不再是幽灵了,被光明正大的纳入数学体系中。
那么基于极限是怎么定义导数的,大家还有印象吗?其实就是基于下面的这个式子:
\[f'(x) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) - f(x)}}{{\Delta x}}\]
数学家学聪明了。先抽象的把什么是导数定义出来(如上式),然后再去图像上讨论切线的含义。这样子一切都完美了。也就是所谓切线,其实就是$\Delta x$趋近于0时,割线的极限。所谓无穷小,就是极限为0的量。还有疑问吗??数学家应该是心里十分痛快的,想大喊一句,还有谁(能挑战我的权威)!!哈哈。那么导数还是切线的斜率,这是没有变的。因此极限的发明本质上是让数学家们手上有了一套可以解释无穷小的理论体系,是一件相当称手的兵器。那么微分是怎么定义呢?就是按照我第一部分将的来定义的。也就是说我微分的定义,不再根据图像上直观来定义了。而是更加抽象了,加入了极限的思想。
其实这里有一个十分十分重要的变化,那就微分的含义看来与之前古典微分学是一样的,但是其本质已经天差地别了。如下:
相同的地方:都是表示微小变化的量。
不同的地方:
(1)古典微分是直接将变化的具体值定义成了微分,也就是直接就是${\rm{dy}} = \Delta y$。但是在极限微分学中是${\rm{dy}} \approx \Delta y$。一个符号的变化,其实就是极限理论的运用。也就是极限微分学中,微分是变化的逼近,而不是变化本身。
(2)极限微分学与古典微分学真的有很多巧合。所以给你造成了很多错觉。但是这一切真的只是巧合,是人为定义造成的。举例如下:
比如古典微分学中把导数直接定义为$f'(x) = \frac{{dy}}{{dx}}$,这是简单粗暴的,没有任何理论体系的搭建的。而在极限微分学中,导数通过极限来定义的,但是巧合的是,我们再通过导数来定义微分后,竟然也能得到$f'(x) = \frac{{dy}}{{dx}}$(具体过程参见本文第一部分)。这真的只是巧合,因此我们也继续称导数就是微商。
另外我们在复函函数求导时,有$\frac{{dy}}{{dx}} = \frac{{dy}}{{dt}}\frac{{dt}}{{dx}}$,咋一看,貌似是将dt约分得到。其实不是这样子的,写成这种形式是经过严格的数学极限证明的(数学分析教材上证明过程),而恰巧竟然跟dt被约分这么像。但是记忆的时候可以当做约分这么来记忆。
我想这也是为什么有时候感觉怪怪的,难以理解的原因吧。
三、开头提到的问题
现在来解决开头提到的问题。你大概知道了那种算法是错误的了吧。那是按照古典微分学的算法来算的(也就是dx在需要为0的时候就为0,不需要的时候就不为)。那么按照极限微分学,怎么算呢?相信学过高等数学的都会算。过程如下:
\[\begin{array}{l}
({x^2})' = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {x + \Delta x} \right) - f(x)}}{{\Delta x}}\\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{(x + \Delta x)}^2} - {x^2}}}{{\Delta x}}
\end{array}\]
我就不算了,上面的结果为2x。
好了,最后做个总结:
(1)古典微分学和极限微分学最本质的区别就是,在前者的体系中,微分就是变化本身,而在后者中,微分是变化的逼近。
(2)微分是实实在在的一个量,是一个无穷小量(当变化趋近于0时)。它也是有自己的运算法则的,参见高等数学教材。其实跟导数的规则差不多。
(3)我们现在所学的体系,是按照先极限、再通过极限定义导数、再通过导数定义微分这个次数来的。但是在历史发展中,是先有的微分(即先定义出dy),然后根据需要(为了解决切线问题)定义出导数的。
(4)至于为什么要把微分定义出来呢?相信如果你以后在数学的领域接触到更高深的知识,就会明白为啥子非得把微分定义出来了。
(5)求微分是求微分,求导是求导。不要因为某些历史造成的巧合就按照自己臆想的规则胡来(比如约分)。当想不明白的时候,多想想极限的思想。
四、导数和微分的区别
最后说一下导数和微分的区别:
导数:是指函数在某一点处变化的快慢,是一种变化率。
微分:是指函数在某一点处(趋近于无穷小)的变化量,是一种变化的量。
而对于多元函数而言,全微分就是指在各个自变量处的微分的和。也就是说总的变化量指各个分变化量的和,这样子就比较容易理解了。比如三元函数,所以dz=zxdx+zydy。
导数和微分的关系类似于速度和路程。也就是说两个变化量之间的比值为衡量变化快慢的变化率。比如速度就是路程的变化量和时间的变化量的比值。而对于一元导数就为y的变化量dy与x的变化量dx之间的比值。