MATLAB教学_13统计
本文学习视频地址:https://www.bilibili.com/video/av68228488?p=13
目录
Central Tendency
Variiation
Variance and standard deviation
21分钟练习
Boxplot
skewness()
kurtosis()
30分钟练习
统计分为 descriptive 和 inferential 两类。
Central Tendency
mean: 加权平均值
mean=( 1+3+5*4+7+9*3+10+13+14)/13=7.31
median: 中间数
median=7
mode:出现频率最多的点
mode= 5
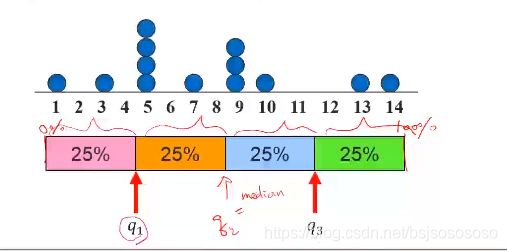
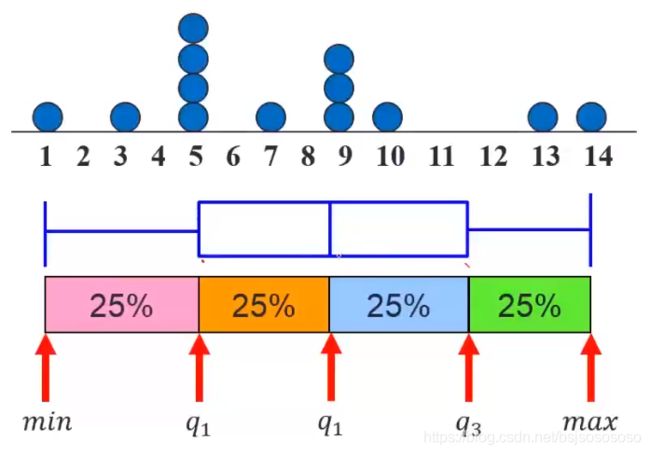
quartile : 上下四分位数
quartile 一般指 q1和 q3。
q1=5; q3=9。
Y = prctile(X,p)返回数据向量或数组X中元素的百分比,表示区间[0,100]中p的百分比。
如果X是一个向量,那么Y就是一个标量,或者是与请求的百分位数(长度(p))相同长度的向量。Y(i)包含p(i)百分位数。
如果X是一个矩阵,那么Y就是一个行向量或矩阵,其中Y的行数等于请求的百分位数(长度(p))。Y的第i行包含X每一列的p(i)百分位数。
对于多维数组,prctile沿着X的第一个非单元素维进行操作。
Variiation
range=13;
Interquartile Range 是 quartile 之间的距离。在这里 q1=5, q3=9。 所以 range =9-5=4;
range 可以用 max() 和 min() 这两个函数来算。
M = max(A)
-
如果
A是向量,则max(A)返回A的最大值。 -
如果
A为矩阵,则max(A)是包含每一列的最大值的行向量。 -
如果
A是多维数组,则max(A)沿大小不等于1的第一个数组维度计算,并将这些元素视为向量。此维度的大小将变为1,而所有其他维度的大小保持不变。如果A是第一个维度长度为零的空数组,则max(A)返回与A大小相同的空数组。
min() 函数于max() 相同。
Variance and standard deviation
variance=(std)^2;
计算 standard 和variance 可以用 std() 和 var()
%%
clear all; clc; %16分钟练习
load stockreturns; %导入数据
x4=stocks(:,4); %导入第4列数据
mean1=mean(x4) %加权平均值
median1=median(x4) %中间值
mode1=mode(x4) %出现频率最多的点
max1=max(x4); min1=min(x4);
range=max(x4)-min(x4) %距离
quartile=prctile(x4,[25 75]) %这里只求了quartile 在 25%和75%的点
Interquartiel=quartile(2)-quartile(1) %q3-q1
var1=var(x4) %variance
std1=std(x4) %standard deviationclear all; clc; %18分钟练习
x=1:14;
freqy=[1 0 1 0 4 0 1 0 3 1 0 0 1 1];
subplot(1,3,1); bar(x,freqy); xlim([0 15]); %条形图
subplot(1,3,2); area(x,freqy); xlim([0 15]); %面积图
subplot(1,3,3); stem(x,freqy); xlim([0 15]); %离散序列图21分钟练习
%%
clear all; clc; %21分钟练习
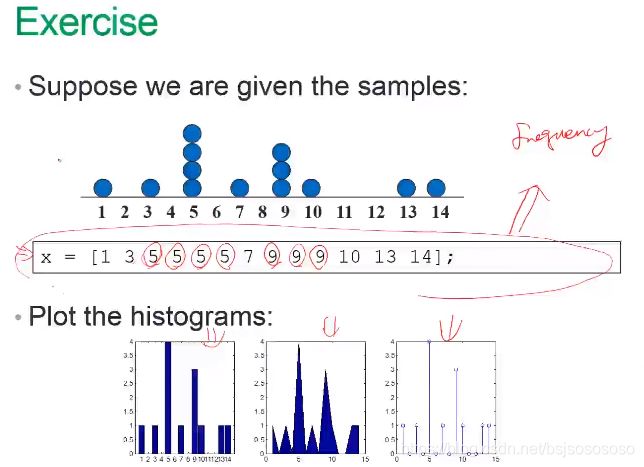
x=[1 3 5 5 5 5 7 9 9 9 10 13 14];
t1=tabulate(x); %转换为频率表
subplot(1,3,1); bar(t1(:,1),t1(:,2));
subplot(1,3,2); area(t1(:,1),t1(:,2));
subplot(1,3,3); stem(t1(:,1),t1(:,2));t1=tabulate(x)
显示向量x中数据的频率表。对于x中的每个惟一值,tabulate函数显示实例数和该值在x中的百分比。
为正整数向量创建一个频率表。默认情况下,如果向量x只包含正整数,那么tabulate将返回0,表示1和max(x)之间的整数在x中不出现。也就是说,如果在这个x 当中,一些数没有的话,依然会返回0。 例如 在x 中有1-14的数,但是没7, 那么7 这一行就返回0。要避免这种行为,请在调用tabulate之前将向量x转换为分类向量。利用 categorical()
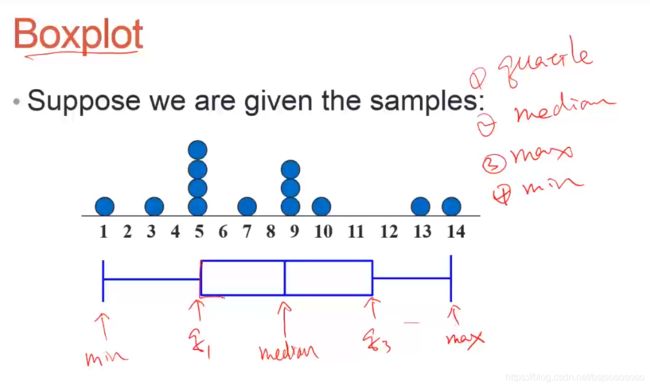
Boxplot
箱型图
clear all; clc; %23分钟练习
marks=[80 81 81 84 88 92 92 94 96 97];
boxplot(marks)
prctile(marks,[25 50 75])skewness()
用于衡量x的对称性。
- 对于正太分布,偏度为0;
- 若偏度为正,则x均值左侧的离散度比右侧弱;
- 若偏度为负,则x均值左侧的离散度比右侧强。
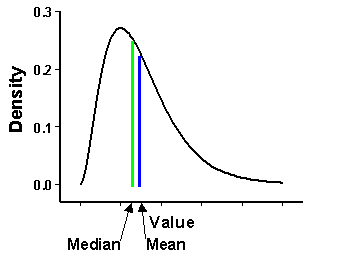
偏态量度对称性。0说明是最完美的对称性,正态分布的偏态就是0。如图2所示,右偏态为正,表明平均值大于中位数。反之为左偏态,为负。
clear all; clc; %39分钟练习
X=randn([10 3])*3;
X(X(:,1)<0,1) =0;
X(X(:,3)>0,3) =0;
boxplot(X)引用博文: http://blog.sciencenet.cn/blog-1148346-786610.html
kurtosis()
峰度(Kurtosis)
峰度衡量数据分布的平坦度(flatness)。尾部大的数据分布,其峰度值较大。正态分布的峰度值为3。其公式如下:
式中, K表示峰度(无量纲); i表示第 i个数值; xbar表示平均值; n是采样数量。
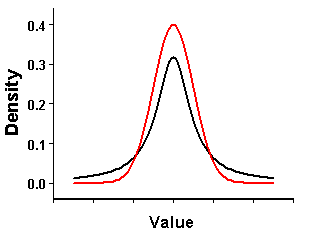
图 1
如图 1所示,黑线服从尖峰(leptokurtic)、厚尾(thick-tailed)分布的峰度值大于3。红线服从正态分布,峰度值等于3。
注意,个别的软件会将峰度值减3,ArcGIS默认正态分布的峰度为3。MS Excel的计算公式与上面略有不同。
引用博文: http://blog.sciencenet.cn/blog-1148346-786610.html
30分钟练习
%%
clear all; clc; %39分钟练习
load stockreturns;
x=stocks;
for i=1:size(x,2)
y(1,i)=skewness(x(:,i)); %把偏态放在第一行
y(2,i)=kurtosis(x(:,i)); %把峰态放在第二行
end
y
boxplot(x)