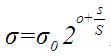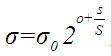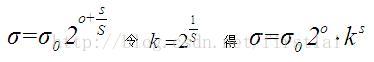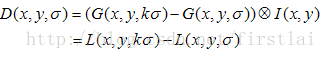图像金字塔

0 序

       图像金字塔实际上是一张图片在不同尺度下的集合，即原图的上采样和下采样。常见的金字塔包括高斯金字塔和拉普拉斯金字塔，但是也有一些其它算法衍生的金字塔，并不一定要高斯模糊。需根据自身应用而定，参考文献0中所述的理由我并不认同。

       图像金字塔更多的是一种构建不同尺度空间的思想，网络上搜索较多的可能是在SIFT算法中的应用了，除此之外，还可以应用在光流中，slam的姿态估计中，还有加速模板匹配等等，更详细的可以参考文献1中所述。

1 高斯金字塔

1.1 为什么构建高斯金字塔？

       [参考文献2 ]

整个高斯金字塔，或者说是差分高斯金字塔是我们确定SIFT特征的基础，让我们首先想想高斯金字塔到底干了一件什么事情，他到底模仿的是什么？答案很容易确定，高斯金字塔模仿的是图像的不同的尺度，尺度应该怎样理解？对于一副图像，你近距离观察图像，与你在一米之外观察，看到的图像效果是不同的，前者比较清晰，后者比较模糊，前者比较大，后者比较小，通过前者能看到图像的一些细节信息，通过后者能看到图像的一些轮廓的信息，这就是图像的尺度，图像的尺度是自然存在的，并不是人为创造的。好了，到这里我们明白了，其实以前对一幅图像的处理还是比较单调的，因为我们的关注点只落在二维空间，并没有考虑到“图像的纵深”这样一个概念，如果将这些内容考虑进去我们是不是会得到更多以前在二维空间中没有得到的信息呢？于是高斯金字塔横空出世了，它就是为了在二维图像的基础之上，榨取出图像中自然存在的另一个维度：尺度。因为高斯核是唯一的线性核，也就是说使用高斯核对图像模糊不会引入其他噪声，因此就选用了高斯核来构建图像的尺度。

[ 我的理解：只是提取SIFT特征时使用的是高斯金字塔，并没有强制规定所有多尺度变换都要基于高斯模糊。那SIFT特征使用高斯金字塔的原因是，作者试图模仿人类的视觉系统，在由近及远观察一个物体时，总是先变模糊（高斯模糊）然后变小（降采样）。至于为什么不是其它模糊，而选择高斯模糊的原因是高斯核是唯一的线性核（这句话不理解）。可以从参考文献3 ]

1.2 八度

       简单说就是基于同一张图片的某一固定分辨率下，做不同的高斯模糊形成的图像的集合。而所有的八度的集合就形成了高斯金字塔。[ 各个高斯模糊有何不同，下面会阐述 ]

1.3 构建高斯金字塔

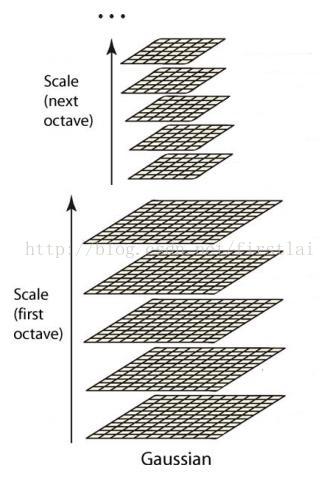
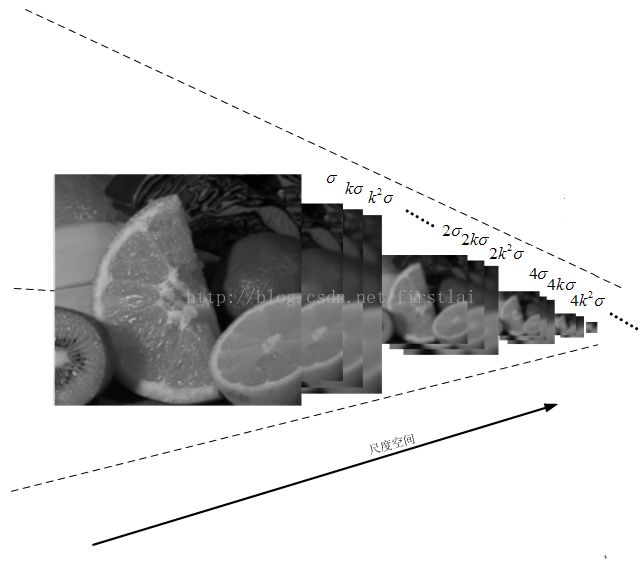
       首先高斯金字塔是由很多个金字塔组成，每个金字塔即为上述的八度集合组成的。而组与组之间的差别在于图像的分辨率，如下图所示。

       高斯金字塔构建过程中，一般首先将图像扩大一倍，在扩大的图像的基础之上构建高斯金字塔，然后对该尺寸下图像进行高斯模糊，几幅模糊之后的图像集合构成了一个八度，然后对该八度下的最模糊的一幅图像进行下采样的过程，长和宽分别缩短一倍，图像面积变为原来四分之一。

       [ 我的理解是逆向的过程，即首先对原图做不同程度的高斯模糊，然后选择最模糊的一幅，做降采样，如此反复。]

1.4 尺度空间

       直观上的解释可见参考文献4。但在这里，尺度不仅体现在空间上，也体现在八度里。在高斯金字塔中，两个变量总结尺度空间。即第几个八度（o）和八度的层数（s），这两个量结合起来就组成了高斯金字塔的尺度。具体量化分析上就是尺度就是高斯模糊时使用的方差sigma。其与o和s的关系如下所示。

       尺度空间也不难理解，首先一个八度中图像的长和宽是相等的，即变量o控制的是塔中尺寸这个尺度；区分同一个尺寸尺度下的图像，就需要s了，s控制了一个八度中不同的模糊程度。这样（o，s）就能够确定高斯金字塔中的唯一一幅图像了，这是个三维空间，两维坐标，一维是图像。

根据lowe的论文，（o，s）作用于一幅图像是通过公式

第一个八度的中图像的尺度分别是δ，kδ，k^2δ......，第二个八度的尺度分别是2δ，2kδ，2k^2δ........，同理第三个八度的尺度分别是4δ，4kδ，4k^2δ........。所以每增加一级八度，δ都要扩大2倍，在一个八度中，k的上标s来区分不同的高斯核。

       Sift算子中σ0取的是固定值1.6。

2 DOG（Difference Of Gause）金字塔

       基于高斯金字塔做进一步特征提取的金字塔，对同一个八度的两幅相邻的图像做差得到插值图像，所有这些图像组成了差分高斯金字塔，SIFT特征点的提取都是基于DOG金字塔完成的。

       DOG金字塔每个八度中都比高斯金字塔少一层，而且效果上由于是差值，可以看到基本上都是非常暗的，如果做归一化后即可清晰看见边缘。

3 尺度空间的连续性

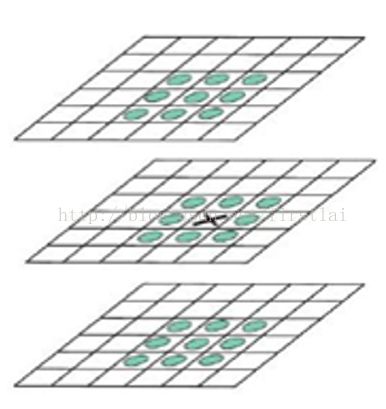
       根据论文所述，为了在每个八度中提取S层的特征点，需要构造S+2张DoG图像。因为特征点是根据极值点所求得的，而每一层的极值点是在三维空间（图像二维，尺度一维）所求（如下图所示），所以对于第0层，以及第S层，需要分别向下以及向上构造一张图像。因此需要s+2张DOG图像，再根据高斯与DOG的关系，可知即需要s+3张高斯模糊的图像。

       一上来就假设“我们要在每个八度中求s层点”，为什么要s层点呢？这才是这个小节的主题：是为了保持尺度的连续性！下面进行详细的分析：

以一个八度中的图像为例说明，高斯函数G对图像I的模糊函数：

高斯差分函数：

通过以上这两个公式，可以确定一个八度中（以第一个八度为例）高斯图像和差分高斯图像的尺度如下（以lowe论文为例，s=3，所以每个八度中会有3+3=6幅图像），每一幅图像的尺度也在图像标示了出来。

在lowe的论文中s=3，因此有

因此，当前八度中各高斯图像的尺度依次为：

σ，2^(1/3)σ，2^(2/3)σ，2^(3/3)σ，2^(4/3)σ，2^(5/3)σ；

当前八度中各差分高斯图像的尺度依次为：

σ，2^(1/3)σ， 2^(2/3)σ，2^(3/3)σ，2^(4/3)σ。

同理，我们可以推断出，下一个八度中各高斯图像的尺度依次为：

2×σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ，2×2^(4/3)σ，2×2^(5/3)σ；

下一个八度中各差分高斯图像的尺度依次为：

2×σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ，2×2^(4/3)σ。

       可以观察到，如果我们取DOG金字塔中的s层的极值点作为特征点，将尺度按序分别按下排列，你不难发现它们是连续的，也就是说如果取s层的极值点，它们都是连续的，保证了尺度的连续性。这一效果带来的直接的好处是在尺度空间的极值点确定过程中，我们不会漏掉任何一个尺度上的极值点，而是能够综合考虑量化的尺度因子所确定的每一个尺度！

2^(1/3)σ，2^(2/3)σ，2^(3/3)σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ，

       最后基于上述讨论可以解释，当s=3时为什么会选择当前八度中的倒数第三层作为下一个八度的第一层。同样也是为了DOG金字塔的尺度的连续性。当s=3时，高斯金字塔的第一个八度的迟度必须是。

       σ，2^(1/3)σ，2^(2/3)σ，2^(3/3)σ，2^(4/3)σ，2^(5/3)σ；

DOG金字塔的第一个八度的尺度为。

σ，2^(1/3)σ，2^(2/3)σ，2^(3/3)σ，2^(4/3)σ。

       为了保证连续性，DOG金字塔的第二个八度中的第二层必须是2×2^(1/3)σ，所以第二个八度的第一层的迟度必须是2×σ，所以高斯金字塔的第二个八度必须是2×σ，这就是第一个高斯金字塔的倒数第三个八度。

       综上，无论是取s层极值点还是取上一级的倒数第三层作为下一级的首个高斯金字塔的首个，都是为了保证尺度的连续性，从而在提取特征点时不会遗漏。

4 OpenCV中常用的API

       OpenCV中使用pyrDown/pyrUp和resize都可以达到缩放图像的目的，区别在于前者是基于高斯模糊然后降采样，而后者是直接通过插值的方法。

5 参考

[0] http://www.ilovematlab.cn/thread-446956-1-1.html

[1] https://www.zhihu.com/question/28748001

[2] http://blog.csdn.net/losteng/article/details/50815322

[3] https://www.zhihu.com/question/19911080

[4] http://www.cnblogs.com/letben/p/5885670.html

[5] http://blog.csdn.net/dcrmg/article/details/52561656