PSIFT:Pore Scale-invariant feature transform;毛孔尺度不变特征点
#Pore-SIFT原理
PSIFT(Pore-Scale-invariant feature transform)是一种检测局部特征的算法,该算法通过求一幅图中的特征点(Interest points,or corner points)及其有关Scale 和 Orientation 的描述子得到特征并进行图像特征点匹配,以得出图像匹配的效果。
构建尺度空间
影像在不同的尺度下用高斯滤波器(Gaussian filters)进行卷积(convolved),然后利用连续高斯模糊化影像差异来找出关键点。关键点是根据不同尺度下的高斯差(Difference of Gaussians,DoG)的最大值(不同于SIFT,这里Pore-SIFT只寻找高斯差最大的关键点)。 由上式可知DoG影像是原始影像与不同尺度倍率的高斯模糊后之差值。Pore-SIFT算法为了求得在不同尺度倍率之下DoG影像的极大值,先将原始影像与不同尺度倍率的高斯模糊进行卷积,这些经高斯模糊处理后的影像依其尺度倍率以2倍为一单位分组,并且通常为一个选定后的定值,因此在每一组内经高斯模糊处理后的影像数量相同,此时将同一组相邻的经高斯模糊处理后的影像两两相减可得其DoG影像Figure 1。
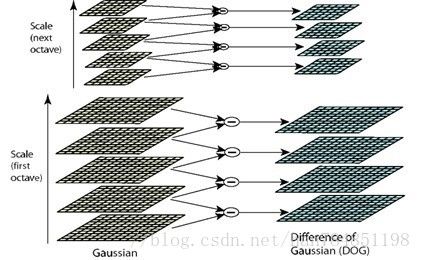
##DOG尺度空间极值检测
在尺度空间中,每一个采样点要和333的邻域内与其他点进行比较,若该点为邻域内的最大值(如Figure 2所示),则将该点作为候选点。由于时在多尺度下寻找的候选点,该候选点为该邻域内的极大值点,利用该点所提取出的特征能具有非常好的尺度不变特征,对于图像小范围的缩放与模糊具有良好的鲁棒性。

边缘响应的去除
在不同尺寸空间下可能找出过多的关键点,有些关键点可能相对不易辨识或易受噪声干扰。Pore-SIFT算法的下一步将会借由关键点附近像素的资讯、关键点的尺寸、关键点的主曲率来定位各个关键点,借此消除位于边上或是易受噪声干扰的关键点。一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率,而在垂直边缘的方向有较小的主曲率。主曲率通过一个2×2 的Hessian矩阵H求出:
(3) H = [ D x x D x y D x y D y y ] H = \left[ \begin{matrix} D_{xx} & D_{xy} \\ D_{xy} & D_{yy} \end{matrix} \right] \tag{3} H=[DxxDxyDxyDyy](3)
T r ( H ) = D x x + D y y = α + β Tr(H)=D_{xx}+ D_{yy}=α+β Tr(H)=Dxx+Dyy=α+β
D e t ( H ) = D x x D y y − D x y 2 = α β Det(H) = D_{xx} D_{yy}-D_{xy}^2=αβ Det(H)=DxxDyy−Dxy2=αβ
曲率满足要求的点应满足如下要求,其中r是给定的阈值,一般取r=10:
T r ( H ) 2 D e t ( H ) < ( r + 1 ) 2 r \frac{Tr(H)^2}{Det(H)}<\frac{(r+1)^2}{r} Det(H)Tr(H)2<r(r+1)2
经过计算后剩余下的点便是下一步的候选点。
计算关键点主方向并旋转
在方位定向中,关键点以相邻相素的梯度方向分布作为指定方向参数,使关键点描述子能以根据此方向来表示并具备旋转不变性。 经高斯模糊处理后的影像 L ( x , y , σ ) L(x,y,σ) L(x,y,σ),在$ σ 尺 寸 下 的 梯 度 量 尺寸下的梯度量 尺寸下的梯度量m(x,y) 与 方 向 与方向 与方向θ(x,y)$可由相邻之像素值计算:
m ( x , y ) = √ ( ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2 ) m(x,y)=√((L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2 ) m(x,y)=√((L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2)
θ ( x , y ) = a r c t a n ( L ( x , y + 1 ) − L ( x , y − 1 ) , L ( x + 1 , y ) − L ( x − 1 , y ) ) θ(x,y)=arctan(L(x,y+1)-L(x,y-1),L(x+1,y)-L(x-1,y)) θ(x,y)=arctan(L(x,y+1)−L(x,y−1),L(x+1,y)−L(x−1,y))
计算每个关键点与其相邻像素之梯度的量值与方向后,为其建立一个以10度为单位36条的直方图。每个相邻像素依据其量值大小与方向加入关键点的直方图中,最后直方图中最大值的方向即为此关键点的方向, 将图像进行正交旋转,旋转至主方向 (Figure 3),确保每个PSIFT特征旋转不变性。
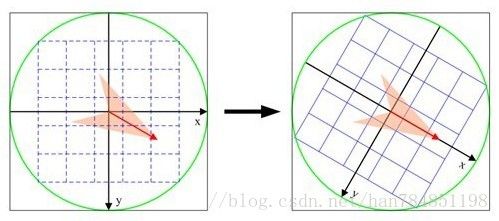
关键点描述子
找到关键点的位置、尺寸并赋予关键点方向后,将可确保其移动、缩放、旋转的不变性。此外还需要建立一个描述子向量,使其在不同光线与视角下皆能保持其不变性。 首先每个88的子区域内建立一个8方向的直方图,在关键点周围2828的区域中一共64个子区域(子区域的大小为44),计算每个像素的梯度量值大小与方向后加入此子区域的直方图中(8个方向)的梯度大小(如图Figure 4所示),共可产生648=512维,并将其归一化,该向量即为关键点的描述子。将每个点提取出的512维特征向量组成一个特征矩阵, 至此形成一张完整图像的Pore-SIFT特征描述符矩阵(大小k*512,k为特征点个数 )
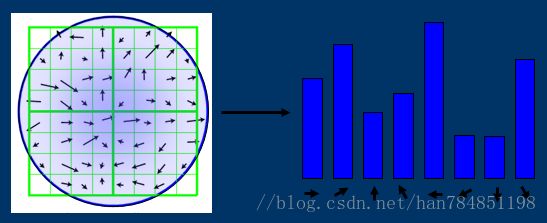
Pore-SIFT特征匹配
得到不同图像的Pore-SIFT特征后,利用特征便可比较两张图像的相似之处,在此使用传统的计算特征欧式距离的方法,生成的Image_A、Image_B两幅图的描述子,(分别是k1512维和k2512维),就将两图中各个scale(所有scale)的描述子进行匹配,匹配上512维即可表示两个特征点匹配上了。实际操作中,为了减少误差,增强鲁棒性,取图像Image_A中的某个关键点,并找出其与图像Image_B中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离小于某个比例阈值,则接受这一对匹配点。降低这个比例阈值,PSIFT匹配点数目会减少,但更加稳定。阈值的取值范围在0.4~0.8之间都是可以接受的,根据不同的需求有不同的取值。
用于人脸匹配有很好的效果。

个人实现的PSIFT的Python代码:https://github.com/BlackJocker1995/PSIFT_python