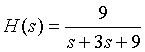信号与系统 Matlab 连续系统分析

MATLAB提供了许多可用于分析线性时不变连续系统的函数，主要包含有系统函数、系统时域响应、系统频域响应等分析函数。

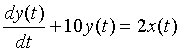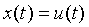1. 已知描述连续系统的微分方程为，输入，初始状态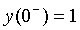，计算该系统的响应，并与理论结果比较，列出系统响应分析的步骤。
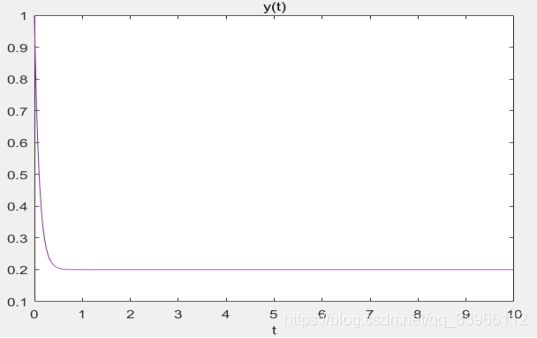
   答：列出系统零状态方程和零输入方程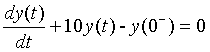，分别求出其零状态响应和零输入响应，叠加后得到系统全响应。然后与理论计算值进行比较。 Matlab程序如下：

a=[1,10]; b0=[1];  b=[2];
t=0:0.01:10;
sys=tf(b0,a);
y1=impulse(sys,t);  %零输入响应
sys1=tf(b,a);
x=(t>=0);
y2=lsim(sys1,x,t);  %零状态响应
y=y1+y2;            %全响应
plot(t,y); 
hold on;
plot(t,0.8*exp(-10*t)+0.2); %理论值
xlabel('t'); title('y(t)');

图中只显示一条曲线，可见程序计算结果与理论值一致。

2.已知连续时间系统的系统函数为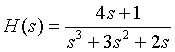，求输入x(t)分别为u(t)，sint*u(t)，时，系统的输出y(t)，并与理论结果比较。
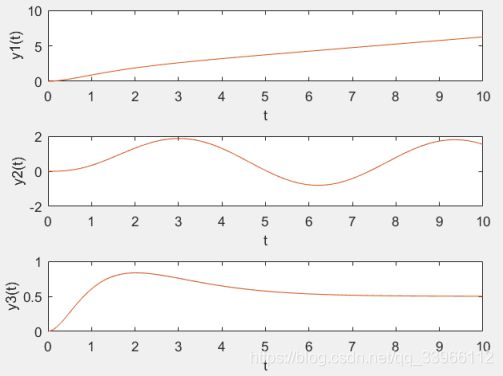
答：经计算，三个输入的响应理论值分别为:

y10(t)=1.25+[0.5*t+7/4*exp(-2*t)-3*exp(-t)]u(t),
y20(t)=0.5+[1.5*exp(-t)-0.7*exp(-2*t)-1.3*cos(t)+0.1*sin(t)]u(t)
y30(t)=0.5+[-4*exp(-t)+3.5*exp(-2*t)+3*t.*exp(-t)]u(t)

Matlab程序如下：

a=[1,3,2,0]; b=[4,1];
t=0:0.1:10;
y10=1.25+0.5*t+7/4*exp(-2*t)-3*exp(-t);  %理论值
y20=0.5+1.5*exp(-t)-0.7*exp(-2*t)-1.3*cos(t)+0.1*sin(t);
y30=0.5-4*exp(-t)+3.5*exp(-2*t)+3*t.*exp(-t);
sys=tf(b,a);
x1=(t>=0);   y1=lsim(sys,x1,t);
x2=sin(t);   y2=lsim(sys,x2,t);
x3=exp(-t);  y3=lsim(sys,x3,t);
subplot(3,1,1);
plot(t,y1,t,y10);
xlabel('t'); ylabel('y1(t)');
subplot(3,1,2);
plot(t,y2,t,y20);
xlabel('t'); ylabel('y2(t)');
subplot(3,1,3);
plot(t,y3,t,y30); 
xlabel('t'); ylabel('y3(t)');

三条输出曲线与理论值重合，说明程序计算结果无误。

3. 研究具有以下零极点的连续系统：
   (a) 1个极点s=—0.1，增益k=1。
   (b) 1个极点s=0，增益k=1。
   © 2个共轭极点，增益k=1。
   (d) 2个共轭极点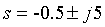，增益k=1。
   (e) 零点在s=0.5，极点在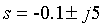，增益k=1。
   (f) 零点在s=0.5，极点在，增益k=1。
   完成下列任务：
   (1)利用zpk和tf命令建立系统的系统函数，画出系统的零极点图。
   (2)分析系统是否稳定。若稳定，画出系统的幅频特性曲线。
   (3)画出系统的冲激响应波形。
   (4)详细列出根据零极点分析系统特性的过程。
   答：因果系统的h(t)是右边信号，其H(s)的ROC必是最右边极点的右边。如果系统稳定，则有。因此H(jw)必存在。意味着H(s)的ROC必然包括jw轴。可以得到：因果稳定系统的H(s)，其全部极点必须位于S平面的左半边。

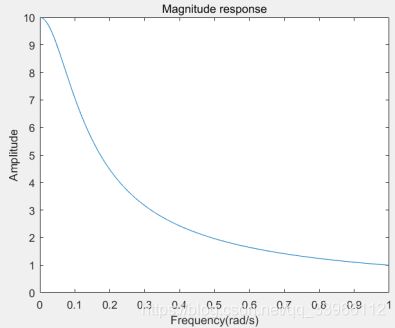
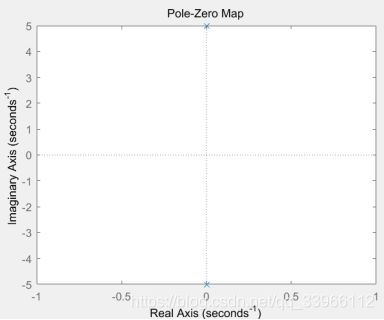
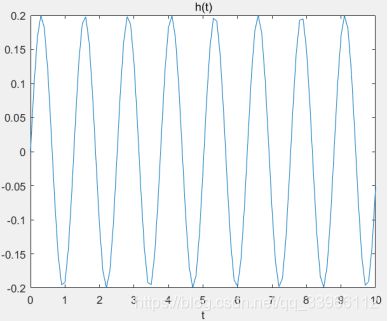
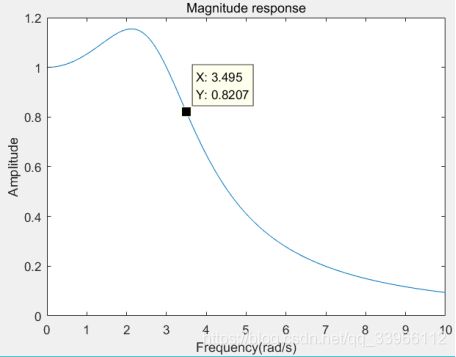
以(f)为例，matlab代码如下：

b=[1,-0.5];  a=conv([1,-0.1+5j],[1,-0.1-5j]);
%零极点图：
z=roots(b);
p=roots(a);
sys=tf(b,a);
pzmap(sys);
%幅频特性：
[H,w]=freqs(b,a);
plot(w,abs(H));
xlabel('Frequency(rad/s)');
ylabel('Amplitude');
title('Magnitude response');
%冲激响应：
t=0:0.1:10;
h=impulse(sys,t);
plot(t,h);
xlabel('t'); title('h(t)')

结果：
（a）零极点图：

极点位于s左半平面，系统稳定。

幅频特性：

冲激响应：

(b)零极点图：

极点位于jw轴，系统不稳定。

冲激响应：

（c）零极点图：

极点位于jw，系统不稳定。

冲激响应：

（d）零极点图：

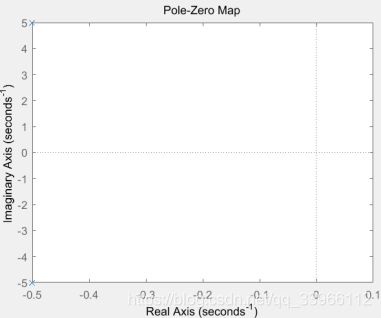
全部极点位于s左半平面，系统稳定。
幅频特性：

冲激响应：

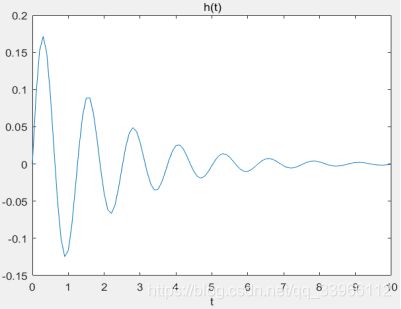
（e）零极点图：

全部极点位于s左半平面，系统稳定。
幅频特性：

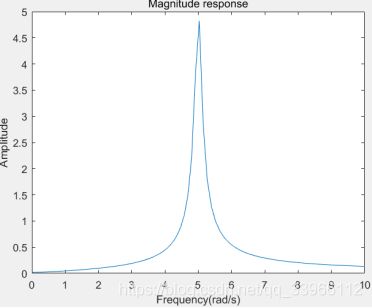
冲激响应：

(f)零极点图：

极点位于s右半平面，系统不稳定。
冲激响应：

4.根据连续系统零极点对系统幅频特性的影响设计下面系统。在S平面上配置零极点，并使用freqs命令绘出相应的幅频特性曲线，重复该过程直至找到满足下面指标的零极点。
(1) 设计一个具有2个零点，2个极点，实系数的高通滤波器，满足; ,。
(2) 设计一个具有实系数的低通滤波器，满足，；
，。
答：（1）

b=[1,0,0];  a=conv([1,1],[1,1]);
[H,w]=freqs(b,a);
plot(w,abs(H));
xlabel('Frequency(rad/s)'); ylabel('Amplitude');

由幅频特性曲线可见设计满足题目要求。

(2)

由幅频特性曲线可见设计满足题目要求。