语音信号处理 | 基于卡尔曼滤波的语音增强算法
文章目录
- 1.概述
- 2.卡尔曼滤波原理
- 被估计的信号
- 离散卡尔曼滤波算法
- 参数选择
- 3.基于卡尔曼滤波的语音增强算法
- 语音模型分析
- 参数确定
- 4.程序实现
- 语音数据的导入、加噪与分帧
- 卡尔曼滤波器参数初始化
- 卡尔曼滤波过程
- 结果可视化
- 5.运行结果与结果分析
- 运行结果
- 结果分析
1.概述
语音增强算法可从信号输入的通道数上分为单通道的语音增强算法与多通道的语音增强算法。单通道语音系统在实际应用中较为常见,如电话,手机等。这种情况下语音与噪声同时存在一个通道中 ,语音信息与噪声信息必须从同一个信号中得出。一般这种语音系统要求噪声比较平稳,以便在非语音段对噪声进行估计,再依据估计出来的噪声对带噪的语音段进行处理。如果系统是一个多通道的语音系统,各个通道之间存在着某些相关的特性,这些相关特性对语音增强的处理十分有利。
单通道语音增强是语音增强的基础,本文将重点研究和实现卡尔曼滤波器,并用于语音增强领域。
2.卡尔曼滤波原理
维纳滤波和卡尔曼滤波都是最小均方误差意义下的最优估计。但是维纳滤波只能在平稳条件的约束下。卡尔曼滤波突破了经典维纳滤波方法的局限性,在非平稳状态下也可以保证最小均方误差估计。在卡尔曼滤波中,引入了系统状态变量和状态空间概念。从状态空间的观点看,状态比信号更广泛、更灵活,非常适合处理多变量系统。卡尔曼滤波器给出了一套在计算机上容易实时实现的最优递推滤波算法,适合处理多变量系统、时变系统和非平稳随机过程,获得了广泛的实际应用,其应用领域包括机器人导航、控制、传感器数据融合甚至包括军事方面的雷达系统以及导弹追踪等。
本节中以下内容参考:http://www.cs.unc.edu/~welch/kalman/
被估计的信号
卡尔曼滤波器用于估计离散时间过程的状态变量 x ∈ ℜ n x\in ℜ^n x∈ℜn。这个离散时间过程由以下离散随机差分方程描述:
x k = A x k − 1 + B u k − 1 + w k − 1 (1) x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\tag{1} xk=Axk−1+Buk−1+wk−1(1)
定义观测变量 z ∈ ℜ m z \in ℜ^m z∈ℜm,得到观测方程:
z k = H x k + v k (2) z_k=Hx_k+v_k\tag{2} zk=Hxk+vk(2)
随机信号 w k w_k wk和 v k v_k vk分别表示过程激励噪声和观测噪声。假设它们为相互独立,正态分布的白色噪声:
p ( w ) ∼ N ( 0 , Q ) (3) p(w)\sim N(0,Q)\tag{3} p(w)∼N(0,Q)(3)
p ( v ) ∼ N ( 0 , R ) (4) p(v)\sim N(0,R)\tag{4} p(v)∼N(0,R)(4)
实际系统中,过程激励噪声协方差矩阵 Q Q Q和观测噪声协方差矩阵 R R R可能随着每次迭代计算而变化。但在这假设他们为常数。
当控制函数 u k − 1 u_{k−1} uk−1或过程激励噪声 w k − 1 w_{k−1} wk−1为零时,差分方程(1)中的 n × n n\times n n×n阶增益矩阵 A A A将过去 k − 1 k−1 k−1时刻状态和现在的 k k k时刻状态联系起来。实际中 A A A可能随时间变化,但在这儿假设为常数。 n × l n\times l n×l阶矩阵 B B B代表可选的控制输入 u ∈ ℜ l u \in ℜ^l u∈ℜl的增益。观测方程(2)中的 m × n m\times n m×n阶矩阵 H H H表示状态变量 x k x_k xk对观测变量 z k z_k zk的增益。实际中 H H H可能随时间变化,但在这假设为常数。
定义 x ^ k − ∈ ℜ n \hat{x}_k^- \in ℜ^n x^k−∈ℜn( − ^- −代表先验, ^ \hat{} ^代表估计)为在已知第 k k k步之前状态的情况下第 k k k步的先验状态估计。定义 x ^ k ∈ ℜ n \hat{x}_k \in ℜ^n x^k∈ℜn为已知观测变量 z k z_k zk时第 k k k步的后验状态估计。由此定义先验估计误差和后验估计误差:
e k − ≡ x k − x ^ k − e_k^- \equiv x_k-\hat{x}_k^- ek−≡xk−x^k−
e k ≡ x k − x ^ k e_k \equiv x_k-\hat{x}_k ek≡xk−x^k
先验估计误差的协方差为:
P k − = E [ e k − e k − T ] (5) P_k^-=E[e_k^-{e_k^-}^T]\tag{5} Pk−=E[ek−ek−T](5)
后验估计误差的协方差为:
P k = E [ e k e k T ] (6) P_k=E[e_k{e_k}^T]\tag{6} Pk=E[ekekT](6)
式(7)构造了卡尔曼滤波器的表达式:先验估计 x ^ k − \hat{x}_k^- x^k−和加权的观测变量 z k z_k zk及其预测 H x ^ k − H\hat{x}_k^- Hx^k−之差的线性组合构成了后验状态估计 x ^ k \hat{x}_k x^k。
x ^ k = x ^ k − + K ( z k − H x ^ k − ) (7) \hat{x}_k=\hat{x}_k^-+K(z_k-H\hat{x}_k^-)\tag{7} x^k=x^k−+K(zk−Hx^k−)(7)
式(7)中观测变量及其预测之差( z k − H x ^ k − z_k-H\hat{x}_k^- zk−Hx^k−)被称为观测过程的残差。残差反映了预测值和实际值之间的不一致程度。
式(7)中 n × m n\times m n×m阶矩阵 K K K叫做卡尔曼增益,作用是使式(6)中的后验估计误差协方差最小。 K K K的一种表示形式为:
K k = P k − H T ( H P k − H T + R ) − 1 (8) K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}\tag{8} Kk=Pk−HT(HPk−HT+R)−1(8)
离散卡尔曼滤波算法
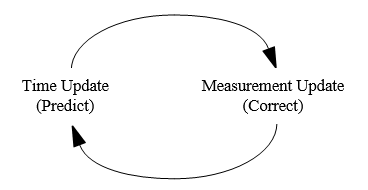
接下来介绍离散卡尔曼滤波算法。卡尔曼滤波器用反馈控制的方法估计过程状态:滤波器估计过程某一时刻的状态,然后以(含噪声的)测量变量的方式获得反馈。因此卡尔曼滤波器可分为两个部分:时间更新方程和测量更新方程。时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值,以便为下一个时间状态构造先验估计。测量更新方程负责反馈――也就是说,它将先验估计和新的测量变量结合以构造改进的后验估计。时间更新方程也可视为预估方程,测量更新方程可视为校正方程。最后的估计算法成为一种具有数值解的预估-校正算法,如下图所示:
时间更新方程为:
x ^ k − = A x ^ k − 1 + B u k − 1 (9) \hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}\tag{9} x^k−=Ax^k−1+Buk−1(9)
P k − = A P k − 1 A T + Q (10) P_k^- = AP_{k-1}A^T+Q\tag{10} Pk−=APk−1AT+Q(10)
状态更新方程为:
K k = P k − H T ( H P k − H T + R ) − 1 (11) K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}\tag{11} Kk=Pk−HT(HPk−HT+R)−1(11)
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) (12) \hat{x}_k=\hat{x}_k^-+K_k(z_k-H\hat{x}_k^-)\tag{12} x^k=x^k−+Kk(zk−Hx^k−)(12)
P k = ( I − K k H ) P k − (13) P_k=(I-K_kH)P_k^-\tag{13} Pk=(I−KkH)Pk−(13)
卡尔曼滤波器工作原理图如下:
参数选择
一般卡尔曼滤波器只需要调整三个参数过程激励噪声协方差 Q Q Q和观测噪声协方差 R R R,其中过程激励噪声协方差 Q Q Q可表示对模型的信任程度, Q Q Q越小,信任程度越高;观测噪声协方差 R R R可表示对观测信息的信任程度, R R R越小,信任程度越高。
参考网址:https://zhuanlan.zhihu.com/p/37750839
3.基于卡尔曼滤波的语音增强算法
语音模型分析
考虑纯净语音:
x ( k ) = s ( k ) + G w ( k ) x(k)=s(k)+Gw(k) x(k)=s(k)+Gw(k)
上式可表述成一个被白噪声驱动的全极点线性系统输出自递归的过程,其p阶AR模型为:
x ( k ) = ∑ i = 1 p a i ( k ) x ( k − i ) + w ( k ) x(k)=\sum_{i=1}^pa_i(k)x(k-i)+w(k) x(k)=i=1∑pai(k)x(k−i)+w(k)
其中, a i ( k ) , i = 1 , … , q a_i(k),i=1,\dots ,q ai(k),i=1,…,q是模型的系数, w ( k ) w(k) w(k)是方差为 σ w 2 \sigma _w^2 σw2和的零均值白噪声过程, p p p是模型的阶次。
考虑加性环境背景噪声构成的含噪语音信号:
y ( k ) = x ( k ) + v ( k ) y(k)=x(k)+v(k) y(k)=x(k)+v(k)
其中, v ( k ) v(k) v(k)是方差为 σ v 2 \sigma _v^2 σv2和的零均值白噪声过程。
将上述模型表示为状态空间形式:
X ( k ) = A X ( k − 1 ) + G w ( k ) y ( k ) = H X ( k ) + v ( k ) X(k) = AX(k-1)+Gw(k)\\y(k)=HX(k)+v(k) X(k)=AX(k−1)+Gw(k)y(k)=HX(k)+v(k)
其中
X ( k ) = [ x ( k − p + 1 ) , x ( k − p + 2 ) , ⋯ , x ( k ) ] T X(k)=[x(k-p+1),x(k-p+2),\cdots ,x(k)]^T X(k)=[x(k−p+1),x(k−p+2),⋯,x(k)]T
H = G T = [ 0 , 0 , ⋯ , 1 ] 1 × p H=G^T=[0,0,\cdots,1]_{1\times p} H=GT=[0,0,⋯,1]1×p
A ( k ) = [ 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 a p ( k ) a p − 1 ( k ) ⋯ a 1 ( k ) ] p × p A(k)=\begin{bmatrix} 0&1&\cdots &0\\ \vdots&\vdots&\vdots&\vdots\\ 0&0&\cdots &1\\ a_p(k)&a_{p-1}(k)&\cdots &a_1(k) \end{bmatrix}_{p\times p} A(k)=⎣⎢⎢⎢⎡0⋮0ap(k)1⋮0ap−1(k)⋯⋮⋯⋯0⋮1a1(k)⎦⎥⎥⎥⎤p×p
上述状态空间形式中, X ( k ) X(k) X(k)为 k k k时刻的状态变量, y ( k ) y(k) y(k)为 k k k时刻的对语音信号的观测值, A A A为状态转移矩阵, H H H为观测系统的参数, w ( k ) w(k) w(k)为过程噪声, v ( k ) v(k) v(k)为观测噪声。
当系统参数已知时,由式 ( 9 ) ( 10 ) ( 11 ) ( 12 ) ( 13 ) (9)(10)(11)(12)(13) (9)(10)(11)(12)(13)可得系统的状态估计:
{ X ^ − ( k ) = A X ^ ( k − 1 ) P − ( k ) = A P ( k − 1 ) A T + G Q G T K ( k ) = P − ( k ) H T ( H P − ( k ) H T + R ) − 1 X ^ ( k ) = X ^ − ( k ) + K ( k ) ( y ( k ) − H X ^ − ( k ) ) P ( k ) = ( I − K ( k ) H ) P − ( k ) \begin{cases} \hat{X}^-(k)=A\hat{X}(k-1)\\ P^-(k) = AP(k-1)A^T+GQG^T\\ K(k)=P^-(k)H^T(HP^-(k)H^T+R)^{-1}\\ \hat{X}(k)=\hat{X}^-(k)+K(k)(y(k)-H\hat{X}^-(k))\\ P(k)=(I-K(k)H)P^-(k)\\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧X^−(k)=AX^(k−1)P−(k)=AP(k−1)AT+GQGTK(k)=P−(k)HT(HP−(k)HT+R)−1X^(k)=X^−(k)+K(k)(y(k)−HX^−(k))P(k)=(I−K(k)H)P−(k)
其中: X ^ − ( k ) \hat X^-(k) X^−(k)为 k k k时刻的先验估计, X ^ ( k ) \hat X(k) X^(k)为 k k k时刻的后验估计, P − ( k ) P^-(k) P−(k)为先验估计误差的协方差矩阵, P ( k ) P(k) P(k)为后验估计误差的协方差矩阵, K ( k ) K(k) K(k)为卡尔曼增益, Q Q Q和 R R R分别为 w ( k ) w(k) w(k)和 v ( k ) v(k) v(k)的协方差矩阵
Q = E ( w ( k ) w ( k ) T ) R = E ( v ( k ) v ( k ) T ) Q=E(w(k)w(k)^T)\\ R=E(v(k)v(k)^T) Q=E(w(k)w(k)T)R=E(v(k)v(k)T)
参数确定
在卡尔曼滤波算法中,必须要有语音模型参数 a ^ = [ a 1 , a 2 , ⋯ , a p ] T \hat{a}=[a_1,a_2,\cdots ,a_p]^T a^=[a1,a2,⋯,ap]T和 σ w 2 \sigma_w^2 σw2及噪声的方差 σ v 2 \sigma_v^2 σv2,因此我们作以下假设:
- 语音用一个20阶的AR模型表示,即 p = 20 p=20 p=20。
- 假定一开始的语音信号中,只含有噪音信号,而无有效语音段,从而求出 σ v 2 \sigma_v^2 σv2,作为噪声的统计先验知识。本文为了方便,直接对加入的噪声求方差。
因为语音增强中的卡尔曼系统是个时变系统,即在状态方程 中,系数 A ( k ) A(k) A(k)是时变的,因此对语音模型 a ^ \hat{a} a^和 σ w 2 \sigma_w^2 σw2的计算只能采用迭代的方法进行计算。具体过程为:对一帧语音信号,直接用线性预测系数(LPC)算法求带噪语音的 a ^ \hat{a} a^和 σ w 2 \sigma_w^2 σw2,将此参数提供给卡尔曼滤波模块,对带噪语音进行滤波,滤波后的信号再用LPC算法求 a ^ \hat{a} a^和 σ w 2 \sigma_w^2 σw2,如此迭代循环,直到语音模型中的残差项小于某个阈值,一般考虑到计算量的问题,迭代次数多为3~6次。本文选择迭代7次
4.程序实现
语音数据的导入、加噪与分帧
本文所用的纯净语音样本包含16条语音(8男8女),采样率为16000,时长约为5秒,噪声采用NOISEX-92数据库中的白噪声,采样率为199800Hz。
%% 导入噪声数据
load noise_data/white.mat;
%% 读取语音
[input, fs] = audioread('voice_data/Ch_F2.wav');
t = (0 : 1/fs : (length(input)-1)/fs)';
首先给出信噪比计算公式
S N R ( s ( t ) , n ( t ) ) = 10 l g ∑ t s 2 ( t ) ∑ t n 2 ( t ) SNR(s(t),n(t))=10lg\frac{\sum_t s^2(t)}{\sum_t n^2(t)} SNR(s(t),n(t))=10lg∑tn2(t)∑ts2(t)
其中: S N R SNR SNR为信噪比,单位为dB; ∑ t s 2 ( t ) \sum_t s^2(t) ∑ts2(t)为纯净语音信号的能量; ∑ t n 2 ( t ) \sum_t n^2(t) ∑tn2(t)为噪声能量。
可求出噪声的缩放倍数 α \alpha α:
α = ∑ t ( s 2 ( t ) ) 1 0 S N R 10 ∑ t n 2 ( t ) \alpha = \sqrt{\frac{\sum_t(s^2(t))}{10^{\frac{SNR}{10}\sum_tn^2(t)}}} α=1010SNR∑tn2(t)∑t(s2(t))
新的噪声信号即可表示为 α n ( t ) \alpha n(t) αn(t),本文中加入信噪比 S N R = 5 d B SNR=5dB SNR=5dB
%% 加噪
SNR = 5; % 加噪信噪比
noise = resample(white, fs, 19980);
noise = noise(1 : length(input));
noise = noise - mean(noise);
signal_power = 1/length(input) * sum(input.*input); % 纯净语音能量
noise_variance = signal_power./(10^(SNR / 10));
alpha = sqrt(noise_variance) / std(noise) % 噪声缩放倍数
noise = alpha .*noise;
noiseInput = input + noise; % 信号相加得到带噪信号
接下来分帧,本文选择帧长为0.05s,帧移为100%,另外本方法不需要进行加窗操作
%% 分帧
winLenSec = 0.05; % 帧长 单位:s
overlap_rate = 1; % 帧移比例0~1
w = floor(winLenSec * fs); % 每帧的样点数
overlap_size = w * overlap_rate; % 帧移的样点数
numFrames = floor((length(input) - w) / overlap_size); % 帧数
framedSignal = zeros(numFrames,w); % 为分帧后的信号分配内存
for i=1:numFrames
interval = (i - 1) * (overlap_size) + (1 : w);
framedSignal(i, :) = noiseInput(interval);%.*hamming(w); % 加窗
end
卡尔曼滤波器参数初始化
对第3节中卡尔曼滤波器的状态估计方程的部分参数进行初始化,需要初始化的滤波器参数有:信号的AR模型系数、过程噪声方差 Q Q Q、观测噪声方差 R R R、误差协方差矩阵 P P P、初始状态估计,其中:
- 信号的AR模型系数和过程噪声方差 Q Q Q需要在卡尔曼滤波过程中进行迭代求解,详见第3节中的参数确定。所以暂时初始化为带噪语音的AR模型系数及方差
- 观测噪声方差 R R R参见第3节中的参数确定,直接使用噪声方差进行初始化
- 误差协方差矩阵 P P P初始化为观测噪声方差
- 初始状态估计使用前AR模型阶数个样点进行初始化
%% 初始化参数
arOrder = 20; % AR模型阶数
numIter = 7; % 求解语音信号的AR模型参数时的迭代次数
H = [zeros(1, arOrder - 1), 1]; % 观测增益矩阵
R = var(noise); % 噪声方差
[arCoeff, Q] = lpc(framedSignal', arOrder); % 每帧带噪语音的AR模型系数arCoeff和方差Q
errCov = R * eye(arOrder); % 后验估计误差协方差矩阵
output = zeros(1, length(noiseInput)); % 为输出信号分配内存
output(1:arOrder) = noiseInput(1 : arOrder, 1)'; % 初始化输出信号,初始化为带噪语音样本前阶数个样本
estOutput = noiseInput(1 : arOrder,1); % 初始化后验估计
卡尔曼滤波过程
按照第3节中卡尔曼滤波器的状态估计方程对每一帧带噪语音信号进行处理,其中包括卡尔曼滤波过程以及语音信号的AR模型参数的迭代求解。
%% 卡尔曼滤波过程
for k = 1:numFrames % 对每一帧进行卡尔曼滤波
oldOutput = estOutput; % 保存该帧迭代前的后验估计
% 初始化开始进行卡尔曼滤波的位置
if k == 1
iiStart = arOrder + 1; % 如果是第一帧,则从第arOrder+1个点开始处理
end
% 迭代求解语音信号的AR模型参数
for iter = 1 : numIter
% 状态变换矩阵
A = [zeros(arOrder - 1, 1), eye(arOrder - 1); fliplr(-arCoeff(k, 2 : end))]; % fliplr:左右翻转
for ii = iiStart : w
% 计算先验估计
aheadEstOutput = A * estOutput;
% 计算先验估计误差的协方差矩阵p-
aheadErrCov = A * errCov * A' + H' * Q(k) * H;
% 计算卡尔曼增益
K = (aheadErrCov * H') / (H * aheadErrCov * H' + R);
% 计算后验估计
estOutput = aheadEstOutput + K * (framedSignal(k, ii) - H * aheadEstOutput);
% 更新输出结果
index = ii - iiStart + arOrder + 1 + (k - 1) * w;
output(index - arOrder + 1 : index) = estOutput';
% 计算后验估计误差的协方差矩阵p
errCov = (eye(arOrder) - K * H) * aheadErrCov;
end
iiStart = 1;
if iter < numIter % 如果AR模型参数迭代还未完成,则恢复第一次迭代前的后验估计,用来进行下一次迭代
estOutput = oldOutput; % 不然会有吱吱声
end
% 使用LPC算法计算上述滤波结果的AR模型系数以及方差
[arCoeff(k , :), Q(k)] = lpc(output((k - 1) * w + 1 : k * w), arOrder);
end
end
output = output';
结果可视化
%% 画出结果
figure
subplot(311);
plot(t, input)
xlabel('Time/s')
ylabel('Amlitude')
title('Clean Speech Signal')
subplot(312);
plot(t, noiseInput)
xlabel('Time/s')
ylabel('Amlitude')
title('Noise-added Signal')
subplot(313);
plot(t, output(1:length(t)))
xlabel('Time/s')
ylabel('Amlitude')
title('Estimated Clean Output Signal')
5.运行结果与结果分析
运行结果
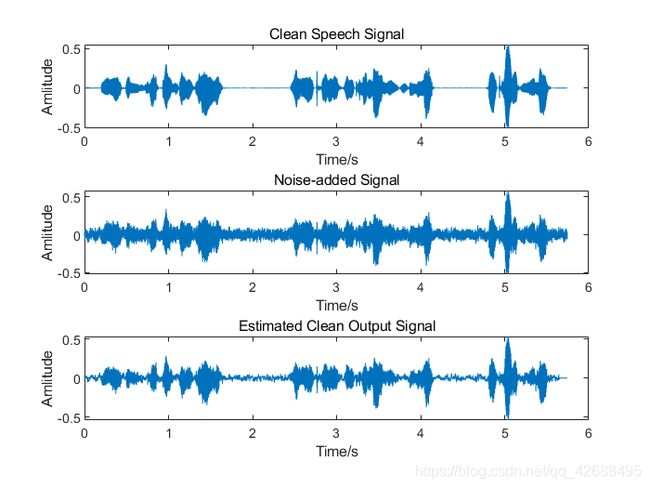
- S N R = 5 d B SNR=5dB SNR=5dB,加入噪声为白噪声
- S N R = − 5 d B SNR=-5dB SNR=−5dB,加入噪声为白噪声
- S N R = 5 d B SNR=5dB SNR=5dB,加入噪声为粉红噪声
- S N R = − 5 d B SNR=-5dB SNR=−5dB,加入噪声为粉红噪声
结果分析
由于时间比较仓促(我懒),所以本文没有使用诸如PESQ等算法对滤波结果进行语音质量评价,所以仅从结果波形上进行总结,当然结果是很明显的。从上述运行结果中,可以看出卡尔曼滤波对白噪声的滤除效果较好,能够很大程度地保留原语音信号的信息,但是对有色噪声的滤除效果较差。
因为卡尔曼滤波的一个假设为:观测噪声是服从均值为0的高斯分布的白噪声。高斯白噪声的功率谱密度服从均匀分布,而有色噪声是指功率谱密度函数不为常数的噪声。所以对于有色噪声,卡尔曼滤波中的一个基本假设:观测噪声是服从高斯分布的白噪声,就不存在了。因此,卡尔曼滤波对有色噪声的滤除效果较差。针对有色噪声,使用粒子滤波(Particle Filter)的效果较好。