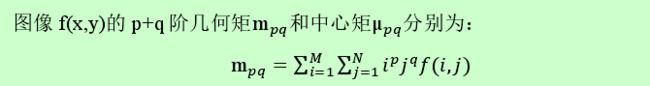【图像处理】——Python+opencv实现图像的hu不变矩特征提取（含原理、推导过程、应用、代码等）

目录

• 转载本文请注明详细地址
• 本文介绍了矩和图像矩的含义
• 本文介绍了不变矩的计算、应用
• 本文介绍了如何计算图像相似度

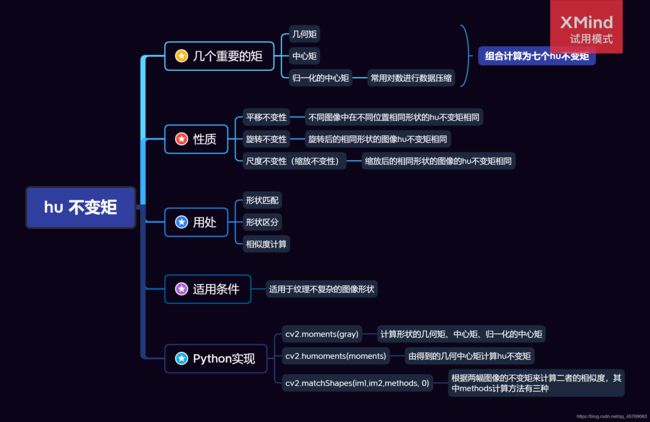
一、思维导图

二、普通矩的定义

1、零阶矩

2、二阶矩

3、二阶以上矩

4、怎么判断是几阶矩

三、什么是图像矩？

四、hu不变矩(cv2.humoments())

1、几何矩

几何矩前几阶的意义

2、中心矩（决定了平移不变性）

3、归一化中心矩（决定了尺度不变性）

4、hu不变矩计算（决定了旋转不变性）

5、hu不变矩的性质

6、hu不变矩的应用与意义

7、适用条件

五、Python+opencv实现不变矩计算

1、自带函数cv2.moments()和cv2.humoments()

2、自定义函数

3、结果

4、 网络上的典型例子

六、形状相似度计算（cv2.matchshapes()）

参数解析：

距离计算方法

自定义距离计算方法

---

一、思维导图

二、普通矩的定义

1、零阶矩

2、二阶矩

3、二阶以上矩

对于三阶或三阶以上矩,使用图像在轴或轴上的投影比使用图像本身的描述更方便。 
三阶矩：投影扭曲，描述了图像投影的扭曲程度。扭曲是一个经典统计量,用来衡量关于均值对称分布的偏差程度。 
四阶矩：投影峰度，峰度是一个用来测量分布峰度的经典统计量。可以计算峰度系数。当峰度系数为0时,表示高斯分布；当峰度系数小于0时,表示平坦的少峰分布；当峰度系数大于0时,表示狭窄的多峰分布。 

4、怎么判断是几阶矩

在计算矩的表达式中，将x,y的指数进行相加，得到的值就是图像矩的阶数

三、什么是图像矩？

最初接触的矩的概念就是力矩的概念，力与距离的乘积叫做力矩。图像矩因为涉及到两个距离x,y，因此是和两个距离、一个像素强度（灰度值有关），具体定义如下：

其中：M、N分别是图像的长宽，f是对应像素点的灰度值

 

四、hu不变矩(cv2.humoments())

1、几何矩

几何矩前几阶的意义

2、中心矩（决定了平移不变性）

3、归一化中心矩（决定了尺度不变性）

比较大的争议是在r的求值上，是否加上1，一般情况下加上1会结果准确些

4、hu不变矩计算（决定了旋转不变性）

5、hu不变矩的性质

图像形状平移不变性

图像形状尺度不变性

图像形状旋转不变性

6、hu不变矩的应用与意义

图像形状匹配

图像形状区分

图像形状相似度计算

7、适用条件

适用于纹理不复杂的图像

五、Python+opencv实现不变矩计算

1、自带函数cv2.moments()和cv2.humoments()

前者输入的是灰度值图像，后者输入的是由几何矩、中心矩、归一化的中心矩组成的一个字典

import cv2
import numpy as np
np.set_printoptions(suppress=True)#定义输出的精度


def sys_moments(img):
    '''
    opencv_python自带求矩以及不变矩的函数
    :param img: 灰度图像，对于二值图像来说就只有两个灰度0和255
    :return: 返回以10为底对数化后的hu不变矩
    '''
    moments = cv2.moments(img)#返回的是一个字典，三阶及以下的几何矩（mpq）、中心矩(mupq)和归一化的矩(nupq)
    humoments = cv2.HuMoments(moments)#根据几何矩（mpq）、中心矩(mupq)和归一化的矩(nupq)计算出hu不变矩
    # 因为直接计算出来的矩可能很小或者很大，因此取对数好比较,这里的对数底数为e,通过对数除法的性质将其转换为以10为底的对数
    humoment = (np.log(np.abs(humoments)))/np.log(10)
    return humoment

2、自定义函数

def def_moments(img_gray):
    '''
    自定义求矩函数，主要是根据公式将一个个参数求出
    :param img_gray:  灰度图像，对于二值图像来说就只有两个灰度0和255
    :return: 返回以10为底对数化后的hu不变矩
    '''
    '''
        由于7个不变矩的变化范围很大,为了便于比较,可利用取对数的方法进行数据压缩;
        同时考虑到不变矩有可能出现负值的情况,因此,在取对数之前先取绝对值
        经修正后的不变矩特征具有平移 、旋转和比例不变性
    '''
    # 标准矩定义为m_pq = sumsum(x^p * y^q * f(x, y))其中f(x,y)为像素点处的灰度值
    row, col = img_gray.shape
    # 计算图像的0阶几何矩
    m00 = img_gray.sum()
    ##初始化一到三阶几何矩
    #计算一阶矩阵
    m10 = m01 = 0
    # 计算图像的二阶、三阶几何矩
    m11 = m20 = m02 = m12 = m21 = m30 = m03 = 0
    for i in range(row):
        m10 += (i * img_gray[i]).sum()#sum表示将一行的灰度值进行相加
        m20 += (i ** 2 * img_gray[i]).sum()
        m30 += (i ** 3 * img_gray[i]).sum()
        for j in range(col):
            m11 += i * j * img_gray[i][j]
            m12 += i * j ** 2 * img_gray[i][j]
            m21 += i ** 2 * j * img_gray[i][j]
    for j in range(col):
        m01 += (j * img_gray[:, j]).sum()
        m02 += (j ** 2 * img_gray[:, j]).sum()
        m30 += (j ** 3 * img_gray[:, j]).sum()
    # 由标准矩我们可以得到图像的"重心"
    u10 = m10 / m00
    u01 = m01 / m00
    # 计算图像的二阶中心矩、三阶中心矩
    y00 = m00
    y10 = y01 = 0
    y11 = m11 - u01 * m10
    y20 = m20 - u10 * m10
    y02 = m02 - u01 * m01
    y30 = m30 - 3 * u10 * m20 + 2 * u10 ** 2 * m10
    y12 = m12 - 2 * u01 * m11 - u10 * m02 + 2 * u01 ** 2 * m10
    y21 = m21 - 2 * u10 * m11 - u01 * m20 + 2 * u10 ** 2 * m01
    y03 = m03 - 3 * u01 * m02 + 2 * u01 ** 2 * m01
    # 计算图像的归一化中心矩
    n20 = y20 / m00 ** 2
    n02 = y02 / m00 ** 2
    n11 = y11 / m00 ** 2
    n30 = y30 / m00 ** 2.5
    n03 = y03 / m00 ** 2.5
    n12 = y12 / m00 ** 2.5
    n21 = y21 / m00 ** 2.5
    # 计算图像的七个不变矩
    h1 = n20 + n02
    h2 = (n20 - n02) ** 2 + 4 * n11 ** 2
    h3 = (n30 - 3 * n12) ** 2 + (3 * n21 - n03) ** 2
    h4 = (n30 + n12) ** 2 + (n21 + n03) ** 2
    h5 = (n30 - 3 * n12) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) + (3 * n21 - n03) * (n21 + n03) \
                                                                                     * (3 * (n30 + n12) ** 2 - (
        n21 + n03) ** 2)
    h6 = (n20 - n02) * ((n30 + n12) ** 2 - (n21 + n03) ** 2) + 4 * n11 * (n30 + n12) * (n21 + n03)
    h7 = (3 * n21 - n03) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) + (3 * n12 - n30) * (n21 + n03) \
                                                                                     * (3 * (n30 + n12) ** 2 - (
        n21 + n03) ** 2)
    inv_m7 = [h1, h2, h3, h4, h5, h6, h7]
    humoments = np.log(np.abs(inv_m7))
    return humoments


def main():
    img = cv2.imread('roi.png',0)
    sys_humoments = sys_moments(img)
    def_humoments = def_moments(img)
    print('自带函数：\n',sys_humoments)
    print('自定义函数：\n',def_humoments)

if __name__ == '__main__':
    main()

3、结果

结果不是很理想，可能在编写计算中心矩和不变矩的公式的时候出现了错误，可以自行纠正

 

4、 网络上的典型例子

可以看到，图像K0.png就是字母K，而S0.png就是字母S。接下来，我们将字母S移到S1中。在s2。png中移动+缩放。我们添加了一些旋转使S3.png，并进一步翻转图像使S4.png。

注意，S0、S1、S2、S3和S4的所有Hu矩的值都很接近，除了S4的最后Hu矩的符号被翻转了。另外，注意它们都与K0非常不同。

六、形状相似度计算（cv2.matchshapes()）

我们将学习如何使用Hu矩来找出两个图形之间的距离。如果距离小，形状的外观接近，如果距离大，形状的外观较远。

OpenCV提供了一个名为matchShapes的实用程序函数，它可以获取两幅图像(或轮廓)，并使用Hu矩查找它们之间的距离。所以，你不需要明确地计算Hu力矩。简单地对图像进行二值化并使用matchShapes。

dist = matchShapes(contour1, contour2, method, parameter)

这里是利用两个图像的不变矩来进行距离的计算

参数解析：

前两个参数是两个图像

method：进行距离计算的方法即公式，分别有以下三种方法

parameter：一般设置为0即可

距离计算方法

注意：以下的计算方法的hu不变矩阵都是经过log函数变换的

两个图像(im1和im2)是相似的，如果上面的距离很小。你可以使用任何距离测量。它们通常产生相似的结果。我个人更喜欢d2。

自定义距离计算方法

七、参考文献

https://zhuanlan.zhihu.com/p/117344473（中文版）

https://www.learnopencv.com/shape-matching-using-hu-moments-c-python/（英文版）

hu不变矩的原理：https://www.researchgate.net/publication/224146066_Analysis_of_Hu's_moment_invariants_on_image_scaling_and_rotation

https://blog.csdn.net/qq_37207090/article/details/83986950

https://blog.csdn.net/qq_23541329/article/details/60963456