Kaldi WFST确定化算法
WFST确定化算法
因为NFA的状态转移不确定,不适合直接做语音识别,在算法实现时往往需要回溯,所以一般使用确定化算法将NFA转换为DFA。确定化算法主要是为了去除空边以及合并具有相同输入的公共边,最终使每个状态对某一个具体的输入,只有一个确定的输出,且每个状态没有空转移,如此可以极大的提升搜索的效率。Kaldi中采用的确定化算法叫“子集构造法”,该算法原本是为了处理FSA的确定化,然而,Kaldi将该算法的思想应用到了WFST上。OpenFST中确定化过程采用了两个独立又相关的算法:空边去除算法和确定化算法,先调用空边去除算法,然后调用确定化算法,但是OpenFST中的空边去除算法只能去除输入输出都为空的边,而子集构造法不仅可以去除输入输出都为空的边,还可以去除仅仅输入为空的边,相比较来说,子集构造法比WFST中的确定化算法在去除空转移方面效果略好。
FSA子集构造法原理
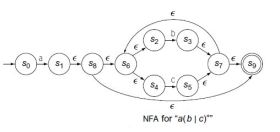
如下图 1(a)所示为一个FSA的NFA。表 1是子集构造法的计算过程,s0的子集仍然是s0,
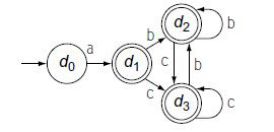
(a)NFA (b)DFA
图 1 FST子集构造法
表 1 FSA子集构造法表
| S(状态) |
D(状态子集) |
终止状态? |
a |
b |
c |
| s0 |
(s0) |
否 |
s1 |
|
|
| s1 |
(s1,s8,s6,s2,s4,s9) |
是 |
|
s3 |
s5 |
| s3 |
(s3,s7,s6,s2,s4,s9) |
是 |
|
s3 |
s5 |
| s5 |
(s5,s7,s6,s2,s4,s9) |
是 |
|
s3 |
s5 |
s1因为空边转移而生成的的子集是(s1,s8,s6,s2,s4,s9),由于s9是终止状态,所以s1的子集也是终止状态;由于s2对输入b转移到s3,所以s1的子集对输入b也转移到s3;由于s4对输入c转移到s5,所以s1的子集对c的转移也到s5。同理,s3因为空边转移而生成的子集是(s3,s7,s6,s2,s4,s9),s5因为空边转移而生成的子集是(s5,s7,s6,s2,s4,s9)。最终将子集(s0)用d0表示,子集(s1,s8,s6,s2,s4,s9)用d1表示,子集(s3,s7,s6,s2,s4,s9)用d2表示,子集(s5,s7,s6,s2,s4,s9)用d3表示,最终生成的DFA如图 1(b)所示,可以看出DFA中去掉了NFA中所有的空边转移,大大减少了状态数。
Kaldi WFST确定化算法原理
简单子集构造法
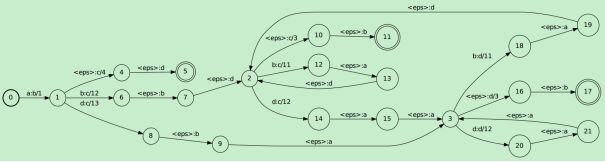
(a)原始WFST
(b)子集构造法后的WFST
(c)结果展开
图 2 Kaldi WFST子集构造法
相比于FSA中每条边只有一个输入,而WFST中有输入、输出和权重三个量,所以在处理上会略有不同。具体过程,如图 2所示,图(a)是原始的WFST, WFST的子集构造法的过程,如表 2
所示:
表 2 WFST子集构造法
| 状态 |
状态子集 |
空转移路径 |
到达状态 |
输出 |
权重 |
| 0号状态 |
{0}:q0 |
|
|
|
|
| q0输入a时进入1号状态 |
{1,2,3,4,6,9}:q1 |
|
q1 |
b |
1 |
| q1输入b时进入5号状态 |
{5,8,9,3,4,6}:q2 |
1->2->3->4 |
q2 |
cbd |
2+3+6+1=12 |
| q1输入d时进入7号状态 |
{7,8,9,3,4,6}:q3 |
1->2->3->6 |
q3 |
cba |
2+3+1+7=13 |
| q1 |
q1 |
1->2->9 |
终止状态 |
cd |
1+2+1=4 |
| q2输入b时进入5号状态 |
q2 |
5->8->3->4 |
q2 |
cad |
1+3+6+1=11 |
| q2输入d时进入7号状态 |
q3 |
5->8->3->6 |
q3 |
caa |
1+3+1+7=12 |
| q2 |
q2 |
5->8->9 |
终止状态 |
cb |
1+1+1=3 |
| q3输入b时进入5号状态 |
q2 |
7->8->3->4 |
q2 |
dad |
1+3+6+1=11 |
| q3输入d时进入7号状态 |
q3 |
7->8->3->6 |
q3 |
daa |
1+3+1+7=12 |
| q3 |
q3 |
7->8->9 |
终止状态 |
db |
1+1+1=3 |
从表中可以看出:WFST的子集构造法,主要是根据输入是否为空进行的,当多个连接的状态输入都为空时,其输出也被合并在一起,同时权重值相加。比如状态1的空转移子集q1是{1,2,3,4,6,9},经过转移“1->2->9”可以到达终止状态,所以q1有一个终止状态的属性,其权重为4,对应的输出为“cd”,同时q1经过“1->2->3->4”可以到达q2状态,其权重为各边的和,为12,经过“1->2->3->6”可以到达q3状态,其权重为13。其他状态之间的转换关系可以以此类推。经过子集构造算法之后的WFST如图 2(b)所示。
语音识别中的WFST的输出一般都只有一个输出,不允许输出字符串,所以还需要对图(b)的结果经常展开处理,其结果如图(c)所示。
Kaldi确定化算法
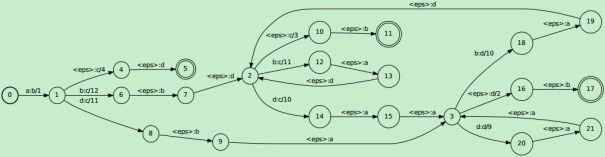
上一节的简单子集构造法针对的例子比较简单,只有空转移的情况,而NFA除了包含空转移的情况,还包含多转移的情况,即针对同一个输入有不同的输出转移。本小节的例子即包含了空转移也包括多转移的情况,如图 4(a)所示,由于确定化过程中的图不容易画出,这里用手写的方式进行演算,确定化过程见图 3,确定化的结果如图 4(b),经过展开后结果是图(c)。这里展示出来的方法和上面简单的子集构造法看似不同,其实都是一样的,上面只是的简化版的WFST子集构造法。这里使用了一个三元组“(残留状态,残留输出,残留权重)”用于表示提取公共输入、公共输出和公共权重之后的残余值,使用这个三元组就可以处理“多转移”的情况。
图 3 空转移和多转移WFST确定化过程
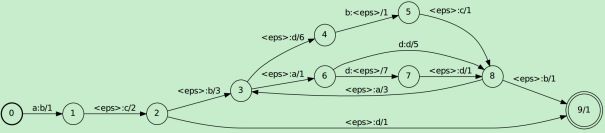
(a)原始WFST
(b)删除多余eps确定化的WFST
(c)将多输出展开为eps之后的WFST
图 4 空转移和多转移