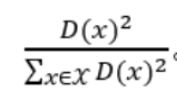聚类算法-----K-means、K-means++
1. K-means
K值的选取方法:
值得一提的是关于聚类中心数目(K值)的选取,的确存在一种可行的方法,叫做Elbow Method(肘部法则):
通过绘制K-means代价函数与聚类数目K的关系图,选取直线拐点处的K值作为最佳的聚类中心数目。
上述方法中的拐点在实际情况中是很少出现的。
比较提倡的做法还是从实际问题出发,人工指定比较合理的K值,通过多次随机初始化聚类中心选取比较满意的结果。
肘部法则如下图:类别个数K为X轴,损失函数值为Y轴:
损失函数的定义如下:
x为样本点,![]() 是类的中心点。下面公式的意义就是:聚类结束后,统计每个样本点x和其对应的类别的中心点的距离,加起来后求平均就得到损失值。
是类的中心点。下面公式的意义就是:聚类结束后,统计每个样本点x和其对应的类别的中心点的距离,加起来后求平均就得到损失值。
我们可以看到,上图中明显出现了拐点,就是 K=3的情况,因此可以设定K=3。
但也有情况就是不出现明显拐点的:
这就要从实际出发,人工设定合理的K值。
代码:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def assignment(df, center, colmap):
#计算所有样本分别对K个类别中心点的距离
for i in center.keys():
df["distance_from_{}".format(i)] = np.sqrt((df["x"]-center[i][0])**2+(df["y"]-center[i][1])**2)
distance_from_centroid_id = ['distance_from_{}'.format(i) for i in center.keys()]
df["closest"] = df.loc[:, distance_from_centroid_id].idxmin(axis=1)#"closest"列表示每个样本点离哪个类别的中心点距离最近
print(df["closest"])
df["closest"] = df["closest"].map(lambda x: int(x.lstrip('distance_from_')))
df["color"] = df['closest'].map(lambda x: colmap[x])
return df
def update(df, centroids):
#更新K个类别的中心点
for i in centroids.keys():
#每个类别的中心点为 属于该类别的点的x、y坐标的平均值
centroids[i][0] = np.mean(df[df['closest'] == i]['x'])
centroids[i][1] = np.mean(df[df['closest'] == i]['y'])
return centroids
def main():
df = pd.DataFrame({
'x': [12, 20, 28, 18, 10, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72, 23],
'y': [39, 36, 30, 52, 54, 20, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24, 77]
})
k = 3
#一开始随机指定 K个类的中心点
center = {
i:[np.random.randint(0,80), np.random.randint(0,80)]
for i in range(k)
}
colmap = {0:"r", 1:"g", 2:"b"}
df = assignment(df, center, colmap)
for i in range(10): #迭代10次
closest_center = df['closest'].copy(deep=True)
center = update(df, center) #更新K个类的中心点
df = assignment(df, center, colmap) #类别中心点更新后,重新计算所有样本点到K个类别中心点的距离
if closest_center.equals(df['closest']): #若各个样本点对应的聚类类别不再变化,则结束聚类
break
plt.scatter(df['x'], df['y'], color=df['color'], alpha=0.5, edgecolor='b')
for j in center.keys():
plt.scatter(*center[j], color=colmap[j], linewidths=6)
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()
if __name__=='__main__':
main()效果:
K-means的缺陷:
1. 聚类种类数K需要提前指定
2.不同初始化的聚类中心可能导致完全不同的聚类结果(针对这点,提出了K-means++,K-means++定义初始聚类中心的规则是初始的聚类中心之间的相互距离要尽可能的远)
2. K-means++
K-means++和K-means的区别就是初始K个类别中心点确定方法不同,K-means是直接随机指定的。而K-means++只随机指定一个类的中心点,然后其余的都按照下面的规则指定。确定后初始的K个类别中心点后,K-means++的后续操作和K-means是一样的。
其实 K-means++和K-means就是选择一开始的k个聚类中心点的方法有差别而已。K-means生成初始聚类中心点的详细过程如下:
1. 定义一个center列表,用来装初始化的聚类中心点。第一个聚类中心点(设为A)也是随机生成的。此时center=[A]
2.然后把所有样本点x(设样本点个数为N)和center里面的中心点算一个距离,若center里有一个点,那么就有1*N个距离,center里有K个点,就有K*N个距离。然后每个样本点都选K个距离中最小的一个,简单地说,就是选最靠近自己的一个。因此N个样本点就会有N个距离,用D(x)表示。
3.我们得到N个样本点对应它最近的聚类中心点的距离D(x)后,就要计算每个样本点可能成为下一个聚类中心点的几率了哦。概率公式在 step2有给出,就是:
这个公式给出的意义就是,离聚类中心点越远的点,越有可能成为下一个聚类中心点。通过这个公式,就可以算出每个样本点x成为下一个聚类中心点的概率P(x)。
4. 有同学可能会说,那么既然概率P都出来了,那么直接拿P最大的点作为聚类中心点不就可以啦?为了撇除噪音的影响,我们不能简单地取最大,而要取较大(当然也是有可能取最大的),所以我们用轮盘法来决定下一个聚类中心点,过程如下:
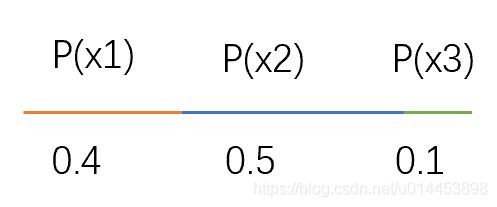
例如我们现在有三个样本点:x1、x2、x3,他们能作为聚类中心点的概率分别如下:
可以看到:x1的区间是0~0.4,x2的区间是0.4~0.9,x3的区间是0.9~1
接下来,我们随机生成一个0~1的数,看看选中的是哪个区间,然后对应区间的点,就是新的聚类中心。
什么用这样的方式呢?我们换一种比较好理解的方式来说明。把D(x)想象为一根线L(x),线的长度就是元素的值。将这些线依次按照L(1),L(2),⋯,L(n)的顺序连接起来,组成长线L。L(1),L(2),⋯,L(n)称为L的子线。 根据概率的相关知识,如果我们在L上随机选择一个点,那么这个点所在的子线很有可能是比较长的子线,而这个子线对应的数据点就可以作为初始聚类中心。
代码:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def select_center(first_center, df, k,colmap):
center = {}
center[0]=first_center
for i in range(1, k):
df = assignment(df,center,colmap)
sum_closest_d = df.loc[:,'cd'].sum() #cd = 最近中心点的距离。把所有样本点对应最近中心点的距离都加在一起
df["p"] = df.loc[:,'cd']/sum_closest_d
sum_p = df["p"].cumsum()
#下面是轮盘法取新的聚类中心点
next_center = random.random()
for index, j in enumerate(sum_p):
if j > next_center:
break
center[i] = list(df.iloc[index].values)[0:2]
return center
def assignment(df, center, colmap):
#计算所有样本分别对K个类别中心点的距离
for i in center.keys():
df["distance_from_{}".format(i)] = np.sqrt((df["x"]-center[i][0])**2+(df["y"]-center[i][1])**2)
distance_from_centroid_id = ['distance_from_{}'.format(i) for i in center.keys()]
df["closest"] = df.loc[:, distance_from_centroid_id].idxmin(axis=1)#"closest"列表示每个样本点离哪个类别的中心点距离最近
df["cd"] = df.loc[:,distance_from_centroid_id].min(axis=1)
df["closest"] = df["closest"].map(lambda x: int(x.lstrip('distance_from_')))
df["color"] = df['closest'].map(lambda x: colmap[x])
return df
def update(df, centroids):
#更新K个类别的中心点
for i in centroids.keys():
#每个类别的中心点为 属于该类别的点的x、y坐标的平均值
centroids[i][0] = np.mean(df[df['closest'] == i]['x'])
centroids[i][1] = np.mean(df[df['closest'] == i]['y'])
return centroids
def main():
df = pd.DataFrame({
'x': [12, 20, 28, 18, 10, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72, 23],
'y': [39, 36, 30, 52, 54, 20, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24, 77]
})
k = 3
colomap = {0: "r", 1: "g", 2: "b"}
first_center_index = random.randint(0,len(df)-1)
first_center = [df['x'][first_center_index], df['y'][first_center_index]]
center = select_center(first_center, df, k,colomap)
df = assignment(df, center, colomap)
for i in range(10): #迭代10次
closest_center = df['closest'].copy(deep=True)
center = update(df, center) #更新K个类的中心点
df = assignment(df, center, colomap) #类别中心点更新后,重新计算所有样本点到K个类别中心点的距离
if closest_center.equals(df['closest']): #若各个样本点对应的聚类类别不再变化,则结束聚类
break
plt.scatter(df['x'], df['y'], color=df['color'], alpha=0.5, edgecolor='b')
for j in center.keys():
plt.scatter(*center[j], color=colomap[j], linewidths=6)
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()
if __name__=='__main__':
main()效果: