深入Python字典的内部实现
字典是通过键(key)索引的,因此,字典也可视作彼此关联的两个数组。下面我们尝试向字典中添加3个键/值(key/value)对:
- >>> d = {'a': 1, 'b': 2}
- >>> d['c'] = 3
- >>> d
- {'a': 1, 'b': 2, 'c': 3}
这些值可通过如下方法访问:
- >>> d['a']
- 1
- >>> d['b']
- 2
- >>> d['c']
- 3
- >>> d['d']
- Traceback (most recent call last):
- File "
" , line 1, in - KeyError: 'd'
由于不存在 'd' 这个键,所以引发了KeyError异常。
哈希表(Hash tables)
在Python中,字典是通过哈希表实现的。也就是说,字典是一个数组,而数组的索引是键经过哈希函数处理后得到的。哈希函数的目的是使键均匀地分布在数组中。由于不同的键可能具有相同的哈希值,即可能出现冲突,高级的哈希函数能够使冲突数目最小化。Python中并不包含这样高级的哈希函数,几个重要(用于处理字符串和整数)的哈希函数通常情况下均是常规的类型:
- >>> map(hash, (0, 1, 2, 3))
- [0, 1, 2, 3]
- >>> map(hash, ("namea", "nameb", "namec", "named"))
- [-1658398457, -1658398460, -1658398459, -1658398462]
在以下的篇幅中,我们仅考虑用字符串作为键的情况。在Python中,用于处理字符串的哈希函数是这样定义的:
- arguments: string object
- returns: hash
- function string_hash:
- if hash cached:
- return it
- set len to string's length
- initialize var p pointing to 1st char of string object
- set x to value pointed by p left shifted by 7 bits
- while len >= 0:
- set var x to (1000003 * x) xor value pointed by p
- increment pointer p
- set x to x xor length of string object
- cache x as the hash so we don't need to calculate it again
- return x as the hash
如果在Python中运行 hash('a') ,后台将执行 string_hash()函数,然后返回 12416037344 (这里我们假设采用的是64位的平台)。
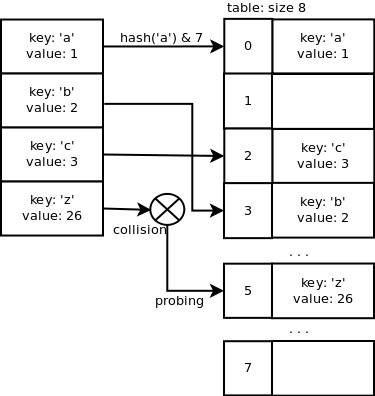
如果用长度为 x 的数组存储键/值对,则我们需要用值为 x-1 的掩码计算槽(slot,存储键/值对的单元)在数组中的索引。这可使计算索引的过程变得非常迅速。字典结构调整长度的机制(以下会详细介绍)会使找到空槽的概率很高,也就意味着在多数情况下只需要进行简单的计算。假如字典中所用数组的长度是 8 ,那么键'a'的索引为:hash('a') & 7 = 0,同理'b'的索引为 3 ,'c'的索引为 2 , 而'z'的索引与'b'相同,也为 3 ,这就出现了冲突。
可以看出,Python的哈希函数在键彼此连续的时候表现得很理想,这主要是考虑到通常情况下处理的都是这类形式的数据。然而,一旦我们添加了键'z'就会出现冲突,因为这个键值并不毗邻其他键,且相距较远。
当然,我们也可以用索引为键的哈希值的链表来存储键/值对,但会增加查找元素的时间,时间复杂度也不再是 O(1) 了。下一节将介绍Python的字典解决冲突所采用的方法。
开放寻址法( Open addressing )
开放寻址法是一种用探测手段处理冲突的方法。在上述键'z'冲突的例子中,索引 3 在数组中已经被占用了,因而需要探寻一个当前未被使用的索引。增加和搜寻键/值对需要的时间均为 O(1)。
搜寻空闲槽用到了一个二次探测序列(quadratic probing sequence),其代码如下:
- j = (5*j) + 1 + perturb;
- perturb >>= PERTURB_SHIFT;
- use j % 2**i as the next table index;
循环地5*j+1可以快速放大不影响初始索引的哈希值二进位的微小差异。变量perturb可使其他二进位也不断变化。
出于好奇,我们来看一看当数组长度为 32 时的探测序列,j = 3 -> 11 -> 19 -> 29 -> 5 -> 6 -> 16 -> 31 -> 28 -> 13 -> 2…
关于探测序列的更多介绍可以参阅dictobject.c的源码。文件的开头包含了对探测机理的详细介绍。
下面我们结合例子来看一看 Python 内部代码。
基于C语言的字典结构
以下基于C语言的数据结构用于存储字典的键/值对(也称作 entry),存储内容有哈希值,键和值。PyObject 是 Python 对象的一个基类。
- typedef struct {
- Py_ssize_t me_hash;
- PyObject *me_key;
- PyObject *me_value
- } PyDictEntry;
下面为字典对应的数据结构。其中,ma_fill为活动槽以及哑槽(dummy slot)的总数。当一个活动槽中的键/值对被删除后,该槽则被标记为哑槽。ma_used为活动槽的总数。ma_mask值为数组的长度减 1 ,用于计算槽的索引。ma_table为数组本身,ma_smalltable为长度为 8 的初始数组。
- typedef struct _dictobject PyDictObject;
- struct _dictobject {
- PyObject_HEAD
- Py_ssize_t ma_fill;
- Py_ssize_t ma_used;
- Py_ssize_t ma_mask;
- PyDictEntry *ma_table;
- PyDictEntry *(*ma_lookup)(PyDictObject *mp, PyObject *key, long hash);
- PyDictEntry ma_smalltable[PyDict_MINSIZE];
- };
字典初始化
字典在初次创建时将调用PyDict_New()函数。这里删掉了源代码中的部分行,并且将C语言代码转换成了伪代码以突出其中的几个关键概念。
- returns new dictionary object
- function PyDict_New:
- allocate new dictionary object
- clear dictionary's table
- set dictionary's number of used slots + dummy slots (ma_fill) to 0
- set dictionary's number of active slots (ma_used) to 0
- set dictionary's mask (ma_value) to dictionary size - 1 = 7
- set dictionary's lookup function to lookdict_string
- return allocated dictionary object
添加项
添加新的键/值对调用的是PyDict_SetItem()函数。函数将使用一个指针指向字典对象和键/值对。这一过程中,首先会检查键是否是字符串,然后计算哈希值,如果先前已经计算并缓存了键的哈希值,则直接使用缓存的值。接着调用insertdict()函数添加新键/值对。如果活动槽和空槽的总数超过数组长度的2/3,则需调整数组的长度。为什么是 2/3 ?这主要是为了保证探测序列能够以足够快的速度找到空闲槽。后面我们会介绍调整长度的函数。
- arguments: dictionary, key, value
- returns: 0 if OK or -1
- function PyDict_SetItem:
- if key's hash cached:
- use hash
- else:
- calculate hash
- call insertdict with dictionary object, key, hash and value
- if key/value pair added successfully and capacity over 2/3:
- call dictresize to resize dictionary's table
inserdict() 使用搜寻函数 lookdict_string() 来查找空闲槽。这跟查找键所用的是同一函数。lookdict_string() 使用哈希值和掩码计算槽的索引。如果用“索引 = 哈希值&掩码”的方法未找到键,则会用调用先前介绍的循环方法探测,直至找到一个空闲槽。第一轮探测,如果未找到匹配的键的且探测过程中遇到过哑槽,则返回一个哑槽。这可使优先选择先前删除的槽。
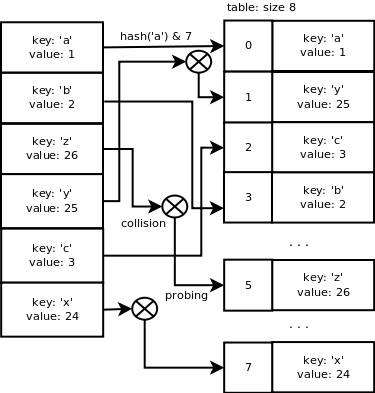
现在我们想添加如下的键/值对:{‘a’: 1, ‘b’: 2′, ‘z’: 26, ‘y’: 25, ‘c’: 5, ‘x’: 24},那么将会发生如下过程:
分配一个字典结构,内部表的尺寸为8。

以下就是我们目前所得到的:
8个槽中的6个已被使用,使用量已经超过了总容量的2/3,因而,dictresize()函数将会被调用,用以分配一个长度更大的数组,同时将旧表中的条目复制到新的表中。
在我们这个例子中,dictresize()函数被调用后,数组长度调整后的长度不小于活动槽数量的 4 倍,即minused = 24 = 4*ma_used。而当活动槽的数量非常大(大于50000)时,调整后长度应不小于活动槽数量的2倍,即2*ma_used。为什么是 4 倍?这主要是为了减少调用调整长度函数的次数,同时能显著提高稀疏度。
新表的长度应大于 24,计算长度值时会不断对当前长度值进行升位运算,直到大于 24,最终得到的长度是 32,例如当前长度为 8 ,则计算过程如8 -> 16 -> 32。
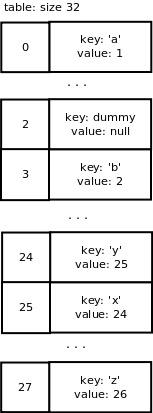
这就是长度调整的过程:分配一个长度为 32 的新表,然后用新的掩码,也就是 31 ,将旧表中的条目插入到新表。最终得到的结果如下:
删除项
删除条目时将调用PyDict_DelItem()函数。删除时,首先计算键的哈希值,然后调用搜询函数返回到该条目,最后该槽被标记为哑槽。
假设我们想要从字典中删除键'c',我们最终将得到如下结果:
注意,删除项目后,即使最终活动槽的数量远小于总的数量也不会触发调整数组长度的动作。但是,若删减后又增加键/值对时,由于调整长度的条件判断基于的是活动槽与哑槽的总数量,因而可能会缩减数组长度。
作者:佚名
来源:51CTO