用Scratch做一个3D引擎

原文：https://www.kidscoding8.com/69969.html

同学们应该都接触过3D游戏和3D动画，那些栩栩如生的画面，大家知不知道其实它们并不是照片，而是通过编程让计算机实时画（计算）出来的呢？今天我们就来学习3D动画的基本原理，以及用scratch实现3D动画的方法。

 

 

3D是英文3-Dimension，是三维的意思的。Dimension就是维度。3D就是指长、宽、高三个维度，或者说由x、y、z三个坐标轴构成的一种空间表示方法。它们构成了一个和我们现实生活一样的立体空间。

 

在计算机科学家的努力下，现代计算机3D技术已经可以达到以假乱真的效果，基本上可以纯粹通过计算来精确重现现实世界或者人们想象中的场景，其精确性、真实性和无限可操作性，使得3D技术可以广泛应用于医学、教育、军事、娱乐等领域。

 

 

大家知道电视机、电脑显示器、手机屏幕等实际上是2D（二维）的平面，它只有长和宽（只有x轴和y轴，没有z轴）。要在2D平面上显示出3D立体效果，就需要“3D引擎”，将立体物体的形状、光线、运动等抽象成数学的表现形式，再通过计算输出2D图像，建立一个个真实的电脑世界。

 

Scratch没有自带的3D引擎。但是只要知道了3D动画背后的原理，我们可以自己制作一个3D引擎出来。这就是我们一直强调的编程的好玩和强大之处：只要你学习、掌握了事物背后的原理，我们就有办法通过编程把它模拟出来。

 

1.    坐标

 

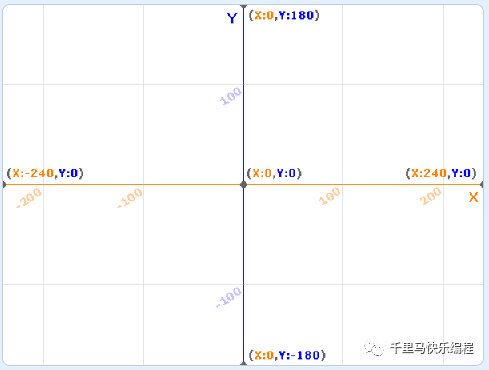
接触过scratch的同学对于2D坐标已经非常熟悉：一个物体的x坐标代表它在屏幕左右方向的位置，y坐标代表它在上下方向的位置。Scratch规定了舞台的坐标范围分别是：x坐标范围在-240到240，y坐标范围在-180到180。

 

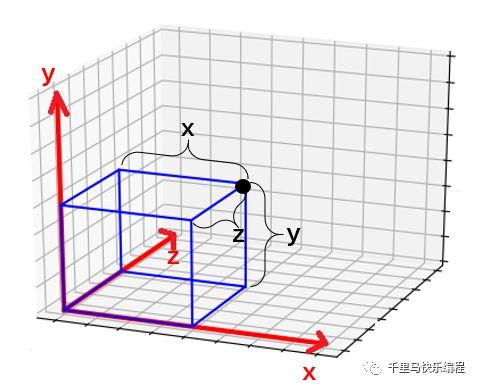
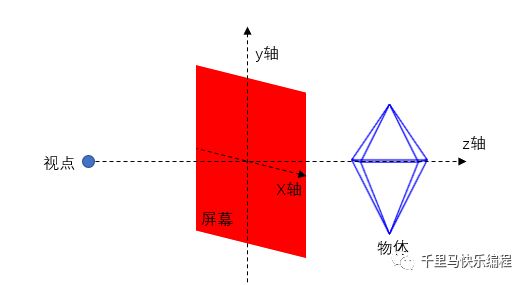
3D坐标系增加了一个z轴，其实就是2D坐标在纵深方向的扩展。如下图所示，红色直线代表x、y、z轴，黑色点的坐标（x,y,z）代表了它在三维立体空间中的位置。

 

 

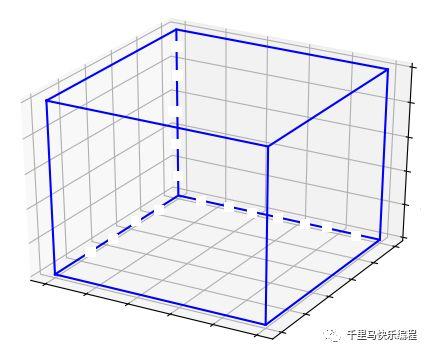
在scratch的2D舞台上画一个四边形，我们需要知道四个顶点的坐标，然后把它们连线就可以画出来。同样道理，如果要在3D空间中画出一个物体，一个方法是知道它的所有顶点的坐标，然后把顶点用直线连起来。比如下面这个立方体，把它的8个顶点连起来就能画出来。

 

事实上，最复杂的3D图案和最真实的3D动画，背后都是通过这种方法画出来。当然画面细节越丰富，背后的数学模型越复杂，也需要越多的计算机资源（CPU、内存、显卡）。作为入门介绍，本文只用最基本的3D图形作为例子。

 

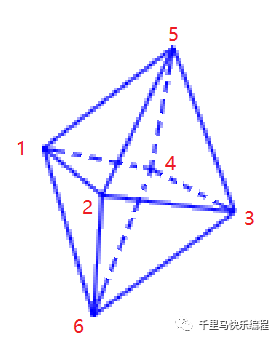
比如下面这个八面体，它有6个顶点，上半部分和下半部分分别有四个三角形。它是最简单的可以一笔画出来的多面体（上面的立方体就不能一笔画出来，而八面体可以，同学们可以思考一下为什么），比如依次连接点1-6-2-5-3-6-4-5-1-2-3-4-1就可以不重复任一条边把它画出来。

简单来说，只要我们知道了八面体的6个顶点的3D坐标，我们就能一笔过把它画出来。

 

2.    投射

 

计算机屏幕是一个2D的平面，我们通过屏幕看到的3D物体，实际上是它根据透视原理在屏幕上的一个2D投射。

 

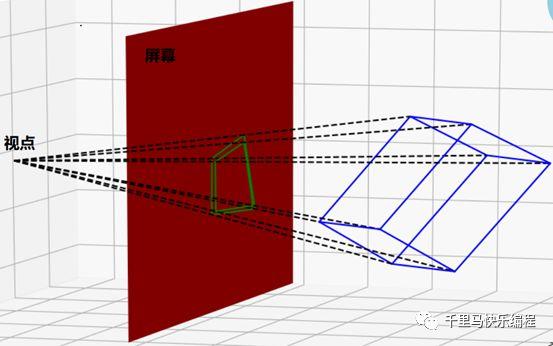
下图说明了这个原理：视点代表了观察者（眼睛或者摄像头）的位置。蓝色是一个3D物体，红色平面代表了屏幕。绿色部分就是3D物体在屏幕上的投射。在屏幕上显示一个3D物体，其实是显示它在2D平面上的投射（绿色部分）。

 

根据上图可以知道，我们在屏幕上看到的一个3D物体的大小和形状，其实跟以下几个因素有关：

• 3D物体的实际位置
• 视点的位置
• 屏幕的位置

 

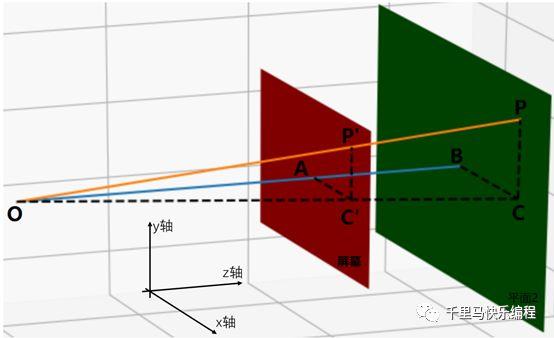
那3D空间某一个点投射在某个2D屏幕上的坐标是怎么计算的呢？请看下图：

 

上图中P代表3D空间中的一个点，设它的位置坐标值是x，y，z。现在要计算的是它在红色的代表屏幕的平面上的投射点P’的坐标值。其中O点代表视点。

 

两次强调，3D点的投射除了和它本身的坐标有关之外，还和视点位置、投射屏幕位置有关。这三个因素是互相影响的。忽略了任何一个因素都不能得出投射点坐标！

 

上图中绿色平面代表P经过的、和红色屏幕平面平行的一个平面。线段OAB和红色以及绿色平面都垂直。为了方便计算，我们让红色平面与x轴和y轴组成的平面平行。这样，线段OAB和z轴平行（并垂直于红色及绿色平面）；线段BC以及AC’与x轴平行；线段PC以及P’C’与y轴平行。

 

因为BC与AC’平行、PC与P’C’平行。根据相似三角形的特点，我们很容易知道：

 

OA /OB = AC’ / BC = P’C’ / PC

 

所以，如果知道：

• P点坐标x,y,z
• O点坐标ox,oy,oz
• 红色平面的z坐标值pz

则：

OA = pz – oz

OB = z – oz

BC = x – ox

PC = y – oy

 

则P在红色屏幕平面投射点P’的x、y轴坐标值为：

 

• P’的x坐标 =
  ox + AC’ =
  ox + [(pz – oz) * (x - ox)/(z - oz)]

   

   

• P’的y坐标 =
  oy + P’C’ =
  oy + [(pz - oz) * (y - oy)/(z - oz)]

 

接下来我们就用这个结论在scratch里画出一个3D的八面体来。

 

Scratch的2D舞台就是上面图中的红色屏幕，我们要做的就是把3D物体在2D屏幕上的投射画出来。所以在画（编程）之前我们先要在自己心中有一个3D坐标，视点的位置、屏幕的位置、物体的位置我们都要先想清楚。

 

 

八面体有6个顶点，如下图依次连接点1-6-2-5-3-6-4-5-1-2-3-4-1就可以一笔过画出它来:

 

 

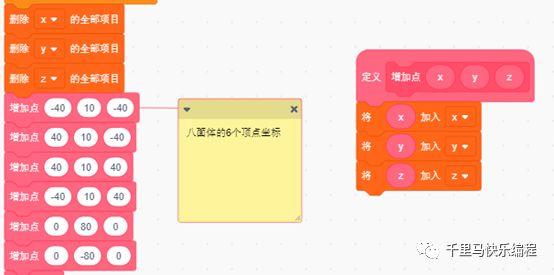
-      首先我们用三个数组分别保存八面体6个顶点的x坐标、y坐标和z坐标：

 

 

-      定义视点及投射屏幕平面的位置（前面说过，为了方便计算，我们让投射平面与x轴和y轴组成的平面平行，所以投射面只有一个z值）

 

 

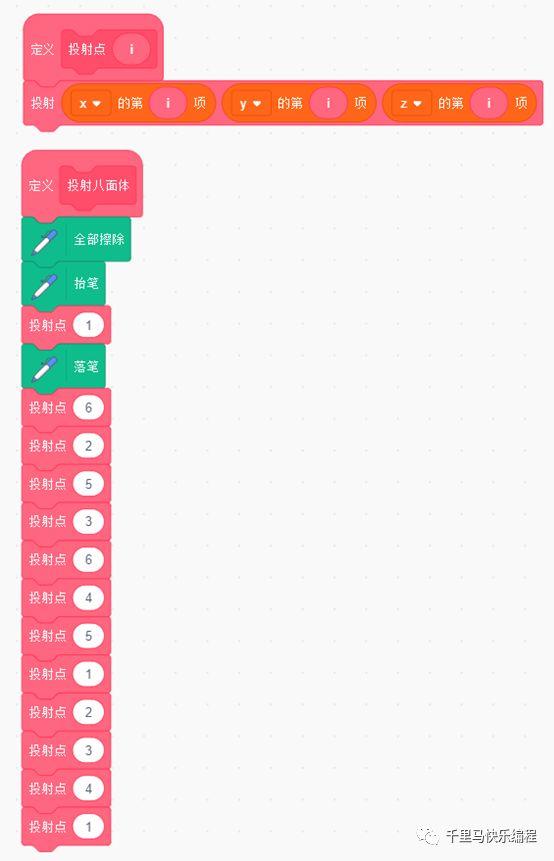
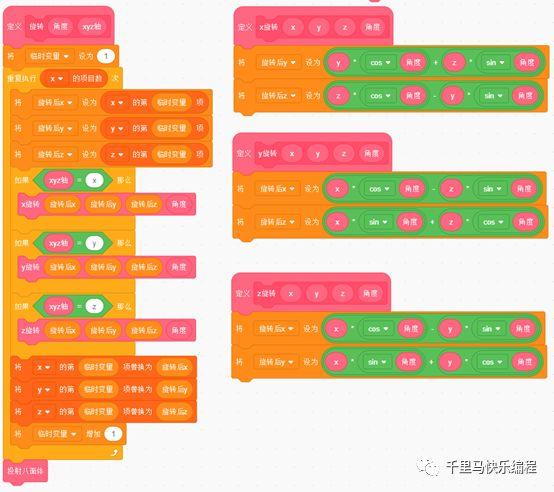
-      根据前面3D到2D屏幕的投射公式，自定义一个积木用来投射转换：

 

-      接下来就依次投射1-6-2-5-3-6-4-5-1-2-3-4-1点，用画笔画出连接各点的轨迹。

 

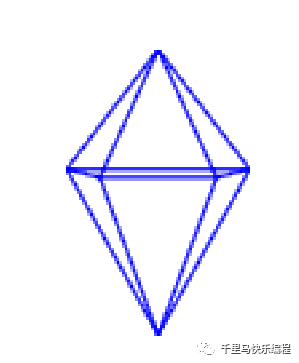
执行“投射八面体“积木就可以画出下面的形状：

 

 

3.    移动

 

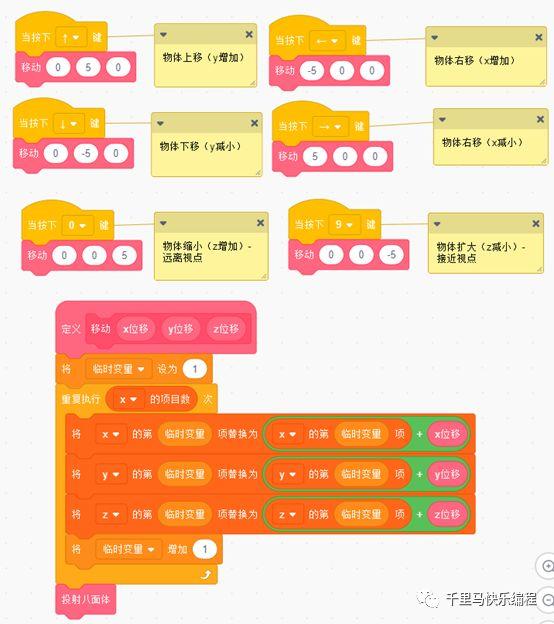
物体移动只需要改变它所有顶点的x,y,z值，然后再重新投射一次就可以了。实现程序如下：

 

注意这里物体的移动是在原3D空间的移动，所以物体在x轴方向或y轴方向移动后，在屏幕上的投射会产生一定的旋转效果。视点离投射平面越近，这种旋转效果越明显。

 

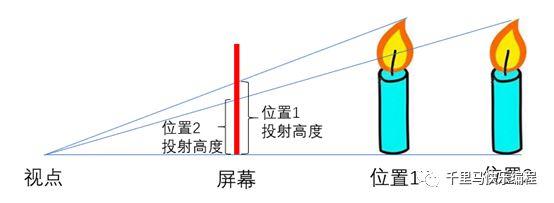
物体在z轴方向的移动会产生物体大小变化的视觉效果：物体远离视点时物体投射缩小，接近视点时物体投射增大。原理如下图所示：

 

移动的效果如下：

 

 

4.    旋转

 

物体旋转涉及到三角函数的知识。推导过程需要一定的篇幅。我们只需要记住简单的结论来应用就可以了。

 

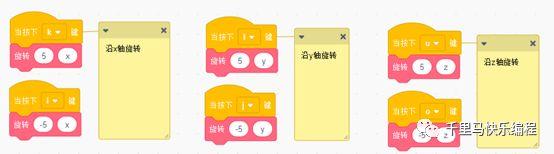
旋转可以分为三种：沿x轴的旋转、沿y轴的旋转和沿z轴的旋转。

 

-      沿x轴旋转时，物体的x坐标不变，y坐标和z坐标的变换规律是(A为旋转角度)：

新的y坐标 = y * cos A + z * sin A

新的z坐标 = z * cos A – y * sin A

 

-      沿y轴旋转时，物体的y坐标不变，x坐标和z坐标的变换规律是(A为旋转角度)：

新的x坐标 = x * cos A – z * sin A

新的z坐标 = x * sin A + z * sin A

 

-      沿z轴旋转时，物体的z坐标不变，x坐标和y坐标的变换规律是(A为旋转角度)：

新的x坐标 = x * cos A – y * sin A

新的y坐标 = x * sin A + y * cos A

 

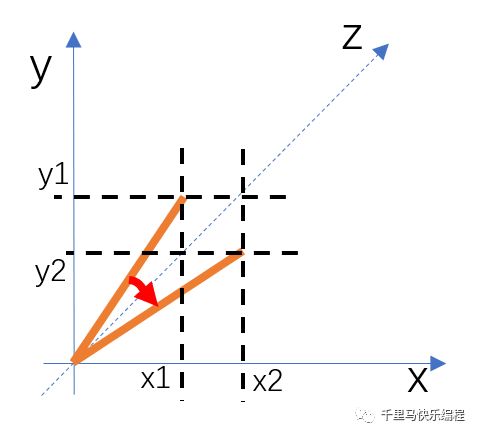
下图显示了沿z轴旋转时的变换情况。有兴趣的同学可以自己推导出坐标的变换规律。

 

注意上面说的坐标变化都是物体原3D坐标的变化，而不是投射在2D平面上的投射坐标的变化。换言之，旋转改变物体坐标后，还要重新计算投射坐标。

 

旋转的实现方法：

 

 

效果如下：

 

 

本文原程序可以在这个链接找到：

https://scratch.mit.edu/projects/282534568/

 

再给大家分享一个3D烟花动画，主要也是运用了本文介绍的方法制作的3D效果。具体的制作方法有时间再给大家分享。

 

https://scratch.mit.edu/projects/282581016/

 

5.    结语

 

今天我们学习了基本的3D引擎制作方法。当然这是最最基本的3D知识，大家看到，即使是最基本的3D原理，已经用到不少的几何和三角函数知识。对有志于研究最新3D技术的同学，比如3D游戏、VR（Virtual Reality虚拟现实）、AR（Augmented Reality增强现实）、3D打印等等，请进一步打好数学和编程基础。

 

事实上3D等图形显示技术属于一门叫做计算机图形学的学科。计算机图形学可以帮助人脑从图形图像的角度理解事物本质。在科学、娱乐、艺术、设计等领域，计算机图形学都起着重要的基础作用。期待有志于此的千里马学员以后能创造出一个又一个的视觉奇迹。