第一张黑洞照片和编程的故事，及用Scratch模拟黑洞

最近全世界的新闻和社交网络都被上面这张“甜甜圏“的照片刷屏了。大家现在都知道这是人类第一次拍到的黑洞的照片。可以说没有计算机科学（编程）就没有这张照片，为什么呢？

 

拍摄黑洞不是易事，如果要用一台天文望远镜看到黑洞，那它的直径至少要有10000千米。因此不少科学家认为拍摄黑洞根本就是不可能完成的任务，毕竟地球直径才13000千米。

 

2017年，还在MIT（就是发明Scratch的MIT-麻省理工学院）读研究生的女计算机科学家Katie Bouman想出了一个计算机算法，可以让分布在世界各地的超级望远镜分别收集黑洞的一部分影像数据，再使用计算机程序把数据整合“拼”到一起。她带领编程团队，经过三年多的努力，终于有了（拼出）这张弥足珍贵的黑洞照片：

 

下图：装着黑洞照片计算程序以及原材料的硬盘，硬盘里的数据足足有五个PB（=5*1024*1024GB）。数据量之大根本无法通过网络传输，必须要用飞机从观测站运回实验室处理：

 

下图：Katie Bouman第一次看到构建中的黑洞照片，掩盖不住的喜悦：

 

Katie Bouman十几岁时就申请了家乡普渡大学的计算机成像研究。从小培养的计算机兴趣和能力，与她今天取得的成就密不可分。

 

今天我们希望用一些中小学生也能明白的语言来解释黑洞、黑洞照片为什么是这个样子，以及用少儿编程工具Scratch来制作一个简化版的黑洞动画（会用到基本的初中数学和物理知识）。下面先从黑洞的产生开始：

 

一． 黑洞知识

 

1. 黑洞的产生

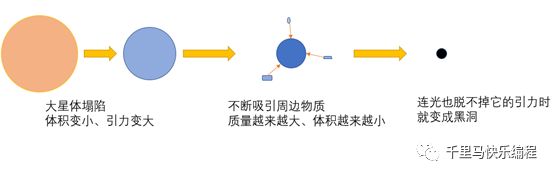
我们知道苹果在地球上会掉落地面是因为万有引力，任何两个物体之间都存在引力，引力会促使物体靠在一起（小物体靠近大的物体）。物体质量越大，它对于其它物体的引力就越强，比如地球比月球质量大，所以同一个物体在地球上会比在月球上的下落速度快。

有一些恒星由于内部燃料耗尽，核心会在自身引力作用下迅速向中心点收缩、塌陷，体积不断变小（质量大体不变）。根据广义相对论，万有引力与质量成正比，与物体间的距离的平方成反比，所以塌陷的星体的吸引力会越来越大，体积越来越小，吸引过来的东西越来越多，并且不断地重复这个过程。

当这个星体质量越来越大，体积越来越小，到达某个临界点时，连经过它附近的光线也无法逃脱它的吸引力被吸进去而出不来的时候，它就成为一个黑洞了。而且这种过程是不断增强的，黑洞质量会越来越大，吞噬越来越多的东西。

2. 史瓦西半径

那么形成黑洞所需要的质量和体积关系的临界点是什么呢？它是一个叫做史瓦西半径的东西，它表示一个固定质量的球状物体要变成黑洞所需要的最大半径。

太阳的史瓦西半径是3公里，就是说如果把太阳的半径缩小到3公里，它就变成一个黑洞；地球的史瓦西半径是9毫米，就是说如果我们能把地球压缩到约一颗花生米这么小，它也能成为一个黑洞了。

3. 黑洞里面是黑的吗？

不知道。

因为进入黑洞史瓦西半径内的任何东西，包括光，都无法再逃脱出来。我们能看到一个物体是因为它自身发射（如太阳）、或反射（如月亮）的光进入到我们眼里。既然连光在黑洞里都出不来了，我们当然无法看到黑洞里面到底是什么颜色，或者里面的物理规律是怎么样的了。

4. 为什么黑洞周围会有光？

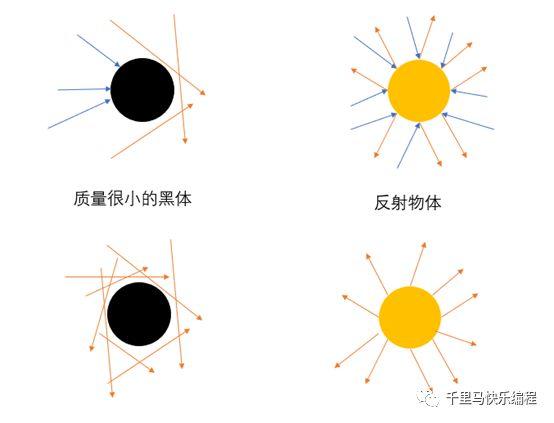
先来说说成像原理：我们能看到一个物体，要么是因为它自身能发出光线，要么是它能够反射光线。现在来考虑不能发射光的物体的情形。

a.    如果它是一个光线无法穿透的黑体，但是质量又没有大到可以改变光的运动轨迹，那么凡是经过它的光会被吸收掉从而看不见，没有经过它的光线则毫不受影响可以完全按原来的轨迹运行。现在假设黑体附近的光源方向是360度都有的，那么看起来黑体所在的位置就会呈现出完全的黑色来。如下图左边部分所示。（蓝色箭头代表看不到的入射光线，橙色箭头代表可以看见的光线）

b.    如果它是可以一个可以反射光线的物体，这就跟我们看到的任何非自发光体一样（如月亮），根据反射原理呈现出物体的轮廓和颜色。如上图右边所示。

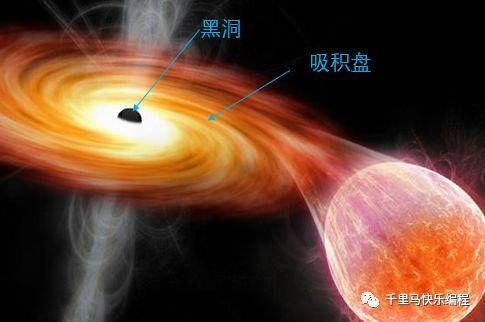
c.    黑洞吸积盘

对于黑洞来说，由于它强大的引力作用，经过它附近的所有物体都会被极速地吸进去，这些物体以接近光速旋转运动、不断高速碰撞摩擦就产生耀眼的光芒，形成一个盘状的旋转结构，叫吸积盘。我们看到的黑洞发光部分，就是吸积盘的成像。

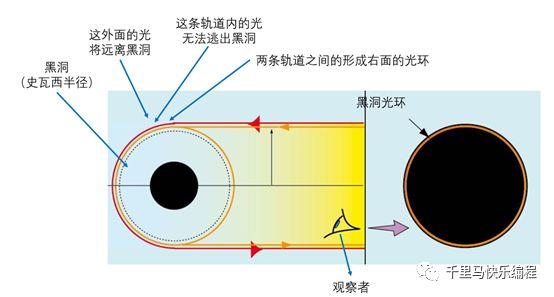
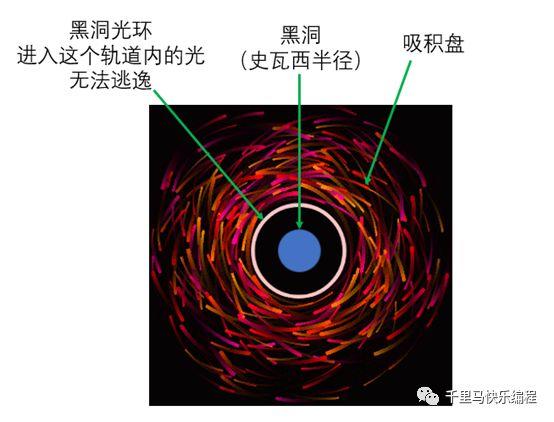
d.    黑洞的光环

黑洞的强大引力会造成时空扭曲，光线通过时也不会走传统意义上的直线。所以我们看到的黑洞中间的黑色部分并不全部是黑洞的史瓦西半径。它是史瓦西半径的约2.6倍的一个轨道。在黑洞的2.6-2.67倍史瓦西半径之间的轨道内会形成一个光环，它是由于黑洞把光扭曲一圏或若干圏后形成的光线集合。原理有点抽象，请看下图：

 

e.    我们可以看到的黑洞

由于黑洞造成的时空扭曲，我们实际看到的黑洞附近的光（吸积盘和黑洞光环）并不会是一个传统意义上的圆盘，而是会根据观察角度不同形成不同的形状。还记得电影《星际穿越》里的黑洞卡冈图亚吗？那就是导演进行了部分美化的近距离黑洞的成像：

吸积盘里的物质由于接近光速会具有强烈的多普勒集束效应，靠近观察者的部分会比较亮。真实的黑洞看起来会更像下面的样子：

 

上面几张图片都是科学家使用高速计算机和复杂的算法模拟出来的。有了黑洞的科学知识，我们使用Scratch和简单的算法，也能做一个简化版的黑洞及其吸积盘动画。下面进入编程环节：

 

二． 编程模拟黑洞

 

1. 我们要创建三个角色：
一个小圆点状的发光物质
一个正圆形的黑洞，外围有一条光亮的边，代表黑洞2.6-2.67倍史瓦西半径的光环。
一个能铺满背景的黑色角色，用来实现渐隐效果：

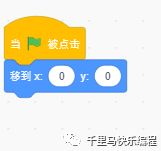
2. 把“黑洞”角色固定在画面正中央：

3. “黑色”角色通过以下指令可以令运动的物体产生渐隐效果。具体原理请参考这篇文章（用Scratch制作烟花 -1.2 渐隐效果）。

 

4. 大部分的程序会在“发光物质”角色上。首先增加以下变量：

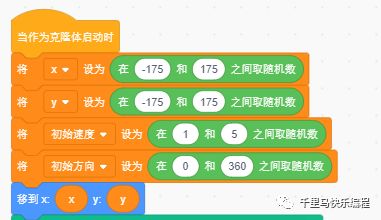
a.       我们使用克隆的方法产生大量的“发光物质”角色，并随机设定发光物质的初始速度、方向和位置值，模拟黑洞附近随机出现的物质。

b.      黑洞引力引起的加速度：
根据广义相对论，两个物体之间的引力和质量成正比，和距离的平方成反比。
而加速度=力/质量，我们这里假设黑洞质量固定，所以加速度只与物质到黑洞的距离有关（和距离的平方成反比），所以我们在程序里可以这样计算发光物质的加速度：

这里的引力常数其实包括了黑洞质量、光速等在动画中不会改变的量。我们只用一个常量来代表就可以。它的值需要根据黑洞大小和物质速度等因素不断测试调整，我这里取的是1000：

 

c.       方向
我们制作的是二维平面的动画，所以速度和加速度都只需要考虑x和y方向。
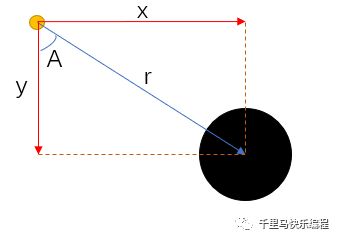
如下图，若蓝色箭头代表速度v，则vx = v * sinA，vy= v * cosA

如果我们知道x,y,r，但不知道角度A，我们也可以用勾股定理计算水平和垂直的速度/加速度。若蓝色箭头代表加速度a，则ax= a * x / r， ay = a * y / r。所以水平、垂直方向的速度和加速度可以这样计算：

 

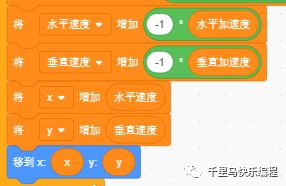
d.      然后我们就可以根据加速度计算出瞬时速度和位移。

如果对于Scratch中位移、速度、加速度的表示方法有疑问，可以参考这篇文章（从“愤怒的小鸟”学习用编程展示物理规律）。

 

e.       我们用画笔画出不同颜色和粗细物体发光的轨迹：

f.        用笔迹的亮度代表速度，速度越快的物质亮度越高

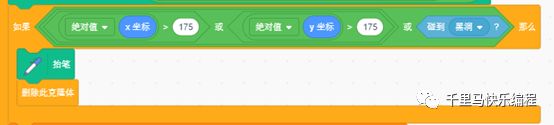
g.      最后，如果一个物质碰到黑洞那它就再也出不来了，我们就删除它。

这是程序运行一段时间后的效果：

源程序可以从这里看到： https://scratch.mit.edu/projects/302538458/

注意：

- 程序必须运行一段时间才能看到吸积盘围绕黑洞旋转的“甜甜圏”的效果。

- 仔细观察还可以发现以下规律：越靠近黑洞引力越大，物质运动得越快，同时也越亮。

- 吸积盘时光扭曲效应这里并没有显示出来。亮度的多普勒集束效应也没有显示。

- 再一次强调，光环内的黑色部分并不是黑洞的全部，只要在2.6倍史瓦西半径内的光都无法被看到。如下图说明：

结语

不论是模拟黑洞，还是给真正的黑洞拍照，都离不开编程。不仅仅是天文学领域，现代几乎所有科学研究的重大突破都离不开计算机科学和编程。希望千里马快乐编程的学员们——不论男女——都能像第一张黑洞照片的功臣Katie Bouman一样，从小学好编程，用好编程，长大后在各个领域发光发亮。

这篇文章要感谢果壳和知乎的黑洞照片专题，还有微博科普帐号：@刘大可先生、@科学家种太阳、@游识猷、@Steed的围脖、@程序员的那些事、@EasyNight，以及Youtube博主Veritasium的有关黑洞介绍视频。Katie Bouman的资料来自CNN、NYTimes。感谢信息时代可以让我们足不出户就能接触大量最新最快的新闻和科学知识。

最后让我们缅怀爱因斯坦、霍金、史瓦西、惠勒等科学家，正是他们的伟大思想引领人类认识了黑洞、以及我们生存的宇宙。