三维视图详解keras.permute_dimensions和numpy.transpose转置效果
二维的转置大家都很熟悉,横轴变纵轴嘛,
1 2 3 1 4 7
4 5 6 转一下变成 2 5 8
7 8 9 3 6 9
但是对于深度学习来说,尤其在transformer以及后来的bert模型出世以后,需要对多个大批次的多个部分的二维数据进行转置,已进行打分机制的计算(Self Attention),那就是4维数据的转置。。。看得人一懵一懵的。所以呢,在下整理了3维的转置3D呈现效果跟大家分享分享,3维转置是个什么空间逻辑,看懂了3维,那4维就按3维的结构进行推导就出来了。
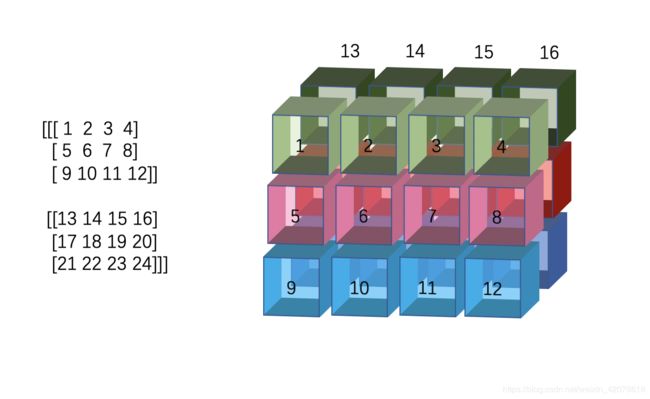
假设我们的数据是这样的三位数据,然后模拟出来的3维结构是这样的(在计算机里,他们其实是列优先的存储结构,这里是为了方便大家直观理解三维的变化,所以以行优先的存储形式展现,比如caffe对图像处理是channel优先,tensorflow是channel最后的数据结构。这些无所谓。咱们的数据可以理解为深度为2,高度为3,宽度为4,即channel优先的2x3x4)
注意!一定要注意数字的顺序
注意!一定要注意数字的顺序
注意!一定要注意数字的顺序
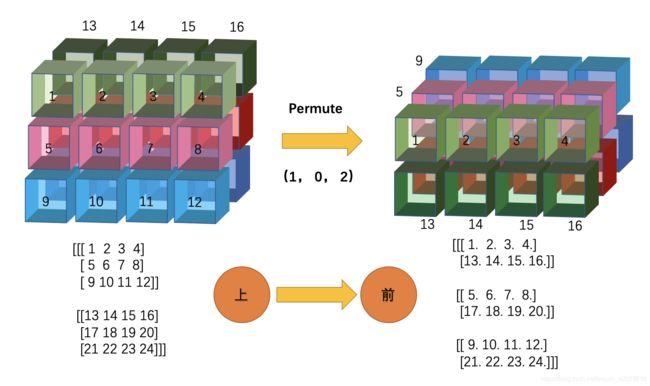
1、深度和高度交换(01交换)
这个转置对应numpy就是np.transpose(x, (1, 0, 2)),,对应keras就是keras.backend.permute_dimensions(x, (1, 0, 2))
我标注的“上——>>>前”的意思就是:
(1)绿色层以1、2、3、4为轴,往前翻转90度
(2)红色层以5、6、7、8为轴,往前翻转90度
(3)蓝色轴以9、10、11、12为轴,往前翻转90度
(4)然后按上述翻转顺序依次从前往后排列,即绿-红-蓝
整个过程就把左图变成了右图。
2、ok没懂,咱们再看一个高度和宽度交换(12交换)
(1)绿色层以1和13为轴,往左旋转
(2)红色层以5和17为轴,往左旋转
(3)蓝色层以9和21为轴,往左旋转
(4)然后按上述翻转顺序依次从左往右排列,即绿-红-蓝
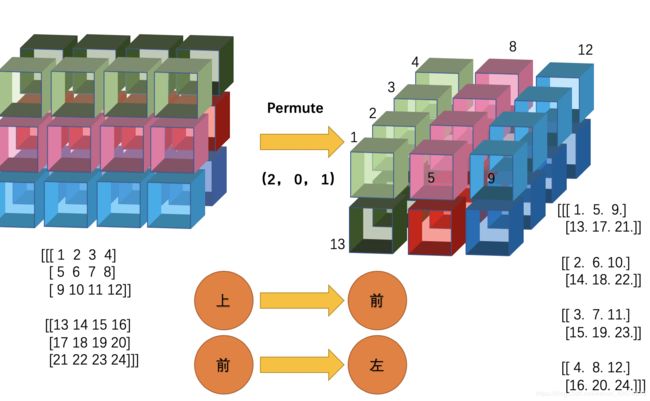
3、再看一个,深度和宽度(02交换)
(1)前排以1、5、9为轴,往左里旋转
(2)后排以13、17、21为轴,往左里旋转
(3)然后按上述翻转顺序依次从左往右排列
4、反正都说到这了,我把剩下的两种情况也都放上来吧
如果你对转置的数学逻辑不清楚,那这五个图,你是能够记住的吧。记住这五个图,你就知道3维的转置是个什么过程了!
什么?
五个还多?
行!
那咱们记前三个!
为什么?
因为,4中的两个图都能从前面3个进行推导!
比如:4-1的图
从(0, 1, 2)到(1, 2, 0)就是先(1, 0, 2),再(0, 1, 2)的过程。
有童鞋问我这里面的0, 1, 2是什么意思,permute(x, (1, 0, 2))在我们的数据里(深度2 x 高度3 x 宽度4)指的是0索引的轴(即深度)跟1索引的轴(即高度)做转置。所以,括号里面的数字,代表的是索引及其对应的度量量!
所以,从(0, 1, 2)到(1, 2, 0)的过程分两步(这只是一种方法):
(1)索引0的值跟索引1的值做交换,变成(1, 0, 2)
(2)再把索引1的值跟索引2的值做交换,变成(1, 2, 0)
图4-2同理,各位自己先推一边,看跟我的结果一样不一样
从(0, 1, 2)到(2, 0, 1)需要经过:
(1)permute_dimensions(x, (2, 1, 0))
(2)permute_dimensions(x, (0, 2, 1))
或
(1)permute_dimensions(x, (0, 2, 1))
(2)permute_dimensions(x, (1, 0, 2))
或
(1)permute_dimensions(x, (1, 0, 2))
(2)permute_dimensions(x, (2, 1, 0))
综上,所有的转置变化,都是基于前3种变化而来的,三维转置是一个比较抽象的数据交换过程,把具象的数字形态转成抽象的空间形态,能让你在对数据的掌控力,更上一层口。
以下代码,各位可以拿去调试调试
import numpy as np
import keras.backend as K
a = np.arange(1, 25).reshape((2, 3, 4))
print(a)
print('===================')
b = K.constant(a)
x = K.permute_dimensions(b, (2, 0, 1))
x1 = K.permute_dimensions(K.permute_dimensions(b, (2, 1, 0)), (0, 2, 1))
x2 = K.permute_dimensions(K.permute_dimensions(b, (0, 2, 1)), (1, 0, 2))
x3 = K.permute_dimensions(K.permute_dimensions(b, (1, 0, 2)), (2, 1, 0))
with K.get_session() as ss:
print(ss.run(x))
print('-----')
print(ss.run(x1))
print('----')
print(ss.run(x2))
print('---')
print(ss.run(x3))