现代密码学(二)——DH密钥协商协议

  DH密钥协商协议即Diffie-Hellman密钥协商算法，DH密钥协商算法在1976年在Whitfield Diffie和Martin Hellman两人合著的论文New Directions in Cryptography（Section Ⅲ PUBLIC KEY CRYPTOGRAPHY）中被作为一种公开秘钥分发系统(public key distribution system)被提出来。并不是用来加密的，而是解决密钥配送的问题，双方就某次通信达成密钥的统一。

一、DH密钥协商协议的流程

  以Alice和Bob为通信双方角色，述阐DH算法的流程。

1）首先Alice与Bob共享一个素数p以及该素数p的本原根g（geneator），当然这里有2⩽g⩽p−1。这两个数是可以不经过加密地由一方发送到另一方，至于谁发送的并不重要，其结果只要保证双方都得知p和g即可。

 2）然后Alice产生一个私有的随机数A，满足1⩽A⩽p−1，然后计算 mod p =  ，将结果Ya通过公网发送给Bob；与此同时，Bob也产生一个私有的随机数B，满足1⩽B⩽p−1，计算 mod p = ，将结果Yb通过公网发送给Alice。

 3）此时Alice知道的信息有p,g,A,，其中数字A是Alice私有的，只有她自己知道，别人不可能知道，其他三个信息都是别人有可能知道的；Bob知道的信息有p,g,B,，其中数字B是Bob私有的，只有他自己知道，别人不可能知道，其他都是别人有可能知道的。

到目前为止，Alice和Bob之间的秘钥协商结束。

Alice通过计算 = mod p得到秘钥，同理，Bob通过计算 = mod p得到秘钥，此时可以证明，必然满足

 = 。因此双方经过协商后得到了相同的秘钥，达成秘钥协商的目的。

 证明：

对于Alice有：

对于Bob有：

可见，Alice和Bob生成秘钥时其实是进行相同的运算过程，因此必然有 = 。"相同的运算过程"是双方能够进行秘钥协商的本质原因，类似的利用椭圆曲线进行秘钥协商也是与之相同的原理。

更严密地考虑，A和B不应该选择p−1，也就是说只能在集合 {1,2,3,...,p−2} 中选择。这是因为如果选择p−1，那么由费马小定理可知，情况就退化成了 的情况，对秘钥协商的机密性构成威胁。

那么窃听者Eve能否破解秘钥呢？首先要知道Eve能够得知哪些信息，显然Eve能够窃听到的信息只能有p,g,,，现在的问题是Eve能够通过以上信息计算出或者吗？要计算或者需要知道A或者B。

以计算A为例，Eve能根据条件 mod p = 计算出A吗？实际上当p是大质数的时候，这是相当困难的，这就是离散对数问题。实际上在论文发表的当时，计算该问题的最有效的算法的时间复杂度大约是。也正是求解该问题在计算上的困难程度保证了DH算法的安全性。如果能够找到对数时间复杂度的算法，那么该算法即容易被攻破。

二：举个例子

1）假设Alice和Bob共享的p和g分别是p = 17,g = 3，显然这里g = 3是p = 17的一个本原根，实际上3,5,6,7,10,11,12,14都是17的本原根。

2）然后Alice选定一个私有数字，假设A=15，计算 =  mod 17 = 14348907 mod 17 = 6，将6发送给Bob；同时Bob也选定一个私有的数字，假设B=13 ，计算 =  mod 17 = 1594323 mod 17 = 12，将12发送给Alice。

3）Alice计算秘钥 =  mod 17 = 2147483647 mod 17 = 8，Bob计算秘钥 =  mod 17 = 2147483647 mod 17 = 8 。双方经过协商后，8最终成为双方的协商的秘钥。

三、存在的问题

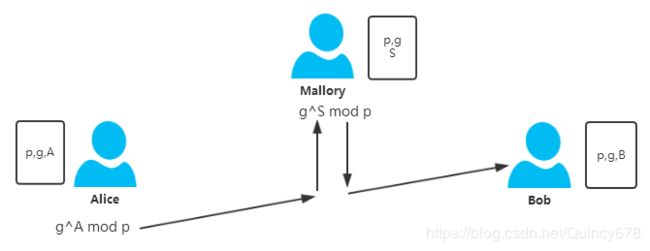
是否DH秘钥协商算法就一定安全呢？应该说也不是，因为存在一种称为中间人攻击，能够对这种秘钥协商算法构成威胁。假设秘钥协商过程中，在Alice和Bob中间有一个称为Mallory的主动攻击者，他能够截获Alice和Bob的消息并伪造假消息，考虑如下情况。

1）Alice和Bob已经共享一个素数p及其该素数p的本原根g，当然Mallory监听到报文也得知了这两个消息。

2）此时Alice计算 =  mod p，然而在将发送给Bob的过程中被Mallory拦截，Mallory自己选定一个随机数S，计算

 =  mod p ，然后将发送给了Bob。

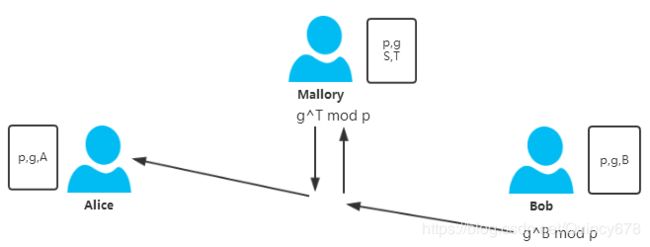
 3）同时Bob计算 =  mod p，然而在将Yb发送给Alice的过程中被Mallory拦截，Mallory自己选定一个随机数T，计算

 =  mod p，然后将发送给了Alice。

  由于通讯消息被替换，Alice计算出的秘钥实际上是Alice和Mallory之间协商秘钥： =  mod p；Bob计算出的秘钥实际上是Bob与Mallory之间协商的秘钥： =  mod p。如果之后Alice和Bob用他们计算出的秘钥加密任何信息，Mallory截获之后都能够解密得到明文，而且Mallory完全可以伪装成Alice或者Bob给对方发消息。