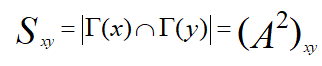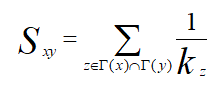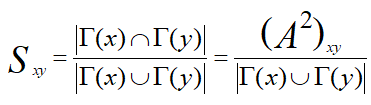链路预测相似性指标计算示例（matlab+python）

        小白笔者最近一段时间在学习链路预测（Link Prediction），在查阅资料的时候，偶然间看到了吕琳媛和周涛合著的《链路预测》这本书，这是一本非常好的书，对经典的链路预测算法讲述的比较清楚，其中为了让读者理解链路预测的含义和计算方法，作者举了一个例子，如下图所示：

图1 示例网络

        在书中，作者用CN指标、RA指标以及Jaccard指标计算节点的相似性。

 

        三种指标的计算公式如下：

        其中表示相似性矩阵，表示网络的邻接矩阵，表示节点的邻居节点的集合，表示节点的邻居节点的集合。

（1）CN指标：

       CN指标是基于局部信息的结构相似性指标，其本质是两个节点的共同邻居越多，两个节点越相似，产生连边的可能性越大，上市实际上计算的是节点之间路径长度为2的数目，这一点比较容易理解，节点与节点他们的公共邻居为，则的路径长度为2，节点与节点之间有几条这样的路径，节点与的CN值就是多少。

（2）RA指标：

        RA指标计算的是节点接收到的资源数，该值即为节点与之间的相似度，此指标计算是，首先要假设每个节点接收到的资源平均分配给它的邻居节点。    

（3）Jaccard指标

 

将上述三种指标应用于图1所示的网络当中，编程实现，代码如下：

matlab的下标是由1开始计数，python的下标由0开始计数，因此两者读入的网络的邻接表的起始下标不同。

一、matlab代码

（1）主函数

clear all
clc
linklist = load( 'ex_linklist.txt');
%------------------------------根据网络的邻接表构造网络的邻接矩阵
linklist( :, 3 ) = 1;          %对无向图，将邻接表将第三列元素置为1
Net = spconvert( linklist );
nodenum = length( Net );
Net( nodenum, nodenum ) = 0;   %此处删除自环，对角元为0以保证为方阵
Net = Net-diag( diag ( Net ));
Net = spones( Net + Net' );    %确保邻接矩阵为对称矩阵
%------------------------------节点相似性
SimCN = CN( Net );
SimJac = Jaccard( Net );
SimRA = RA( Net );
%----------------------------- 采用全矩阵形式表示
Net1 = full( Net );
SimCN1 = full( SimCN );
SimJac1 = full( SimJac );
SimRA1 = full( SimRA );

（2）Common_Neighbors指标

function [ sim ] = CN( matrix )
%计算CN指标
%matrix-网络的邻接矩阵，sim-相似性矩阵
    sim = matrix * matrix;        
end

（3）RA指标

function [ sim ] = RA( matrix )   
%计算RA指标
%net-网络的邻接矩阵，sim-相似性矩阵
    sim1 = matrix ./ repmat( sum ( matrix, 2 ), [1, size( matrix, 1 ) ] ); 
    sim1(isnan(sim1)) = 0; 
    sim1(isinf(sim1)) = 0;
    sim = matrix * sim1;
end

（4）Jaccard指标

function[ sim ] = Jaccard( matrix )
%计算Jaccard指标
%net-网络的邻接矩阵，sim-相似性矩阵
    sim = matrix * matrix;                              %分子，CN             
    deg_row = repmat( sum( matrix, 1 ), [size( matrix, 1 ),1 ] );%节点的度
    deg_row = deg_row .* spones(sim);             %只需保留分子不为0对应的元素
    deg_row = triu( deg_row ) + triu( deg_row' );     %节点对(x,y)的两节点的度之和
    sim = sim ./ ( deg_row .* spones( sim ) - sim );         
    % 计算相似度矩阵 节点x与y并集的元素数目 = x与y的度之和 - 交集的元素数目
end

 

 

 

二、python代码：

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
#--------------------------------------------
def Common_Neighbors( matrix ):
    #计算CN指标
    #matrix-网络的邻接矩阵，sim-相似性矩阵
    sim = np.dot( matrix, matrix )
    return sim
#--------------------------------------------
def RA( matrix ):
    #计算RA指标
    #matrix-网络的邻接矩阵，sim-相似性矩阵
    add_row = matrix.sum( axis = 1 )           #行求和
    add_row_matrix = np.tile( add_row, (( matrix.shape )[0]) )
    sim = adjacent_matrix / add_row_matrix     #节点权重
    sim = matrix * sim
    return sim 
#-------------------------------------------   
def Jaccard( matrix ):
    #计算Jaccard指标
    #matrix-网络的邻接矩阵，sim-相似性矩阵
    sim = matrix * matrix
    sim1 = sim.copy()                          #深复制，sim1与sim指向不同内存
    sim1[ np.nonzero( sim1 ) ] = 1             #分子
    deg_row = matrix.sum( axis = 0 )           #行求和得节点度
    deg_row_matrix = np.tile( deg_row, ( (matrix.shape)[0], 1) )
    deg_row_matrix = np.multiply( deg_row_matrix, sim1 )
    deg_row_matrix = np.triu( deg_row_matrix ) + np.triu( (deg_row_matrix.T) )
    sim = sim / ( np.multiply( deg_row_matrix, sim1 ) - sim )
    return sim
#-------------------------------------------
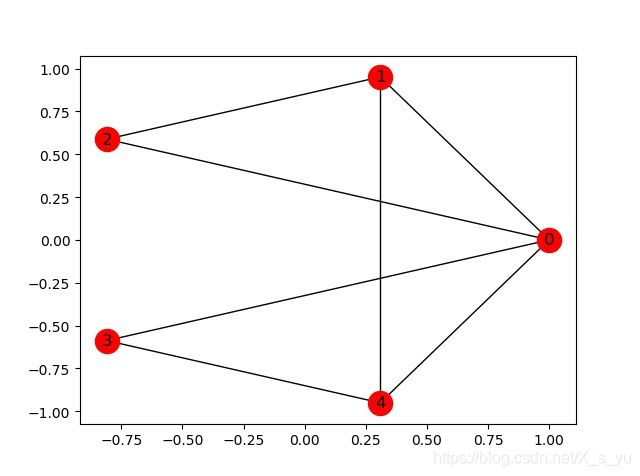
G = nx.read_adjlist( 'linklist.txt' )        #无向图 
adjacent_matrix = nx.to_numpy_matrix( G )    #邻接矩阵
#--------------------------------------------绘图
nx.draw_networkx(G, pos=nx.circular_layout(G), with_labels = True )
plt.show()
#--------------------------------------------节点相似性
CN_sim = Common_Neighbors( adjacent_matrix )
RA_sim = RA( adjacent_matrix )
Jac_sim = Jaccard( adjacent_matrix )

 

使用Networkx创建的网络如图所示：

图2 networkx创建的网络

由于本人初步涉及Networkx库对于该库的绘制网络的函数不甚了解，因此节点的标签默认为由0开始。

参考资料：

[1]吕琳媛,周涛.链路预测[M].高等教育出版社:北京,2013:57-74，289-307.