2.14 子数组之和的最大值
1. 前言
本文的一些图片, 资料 截取自编程之美
2. 问题描述
3. 问题分析
对于这种求优问题, 最基本的思路, 无疑便是穷举了
解法一 : 使用left, right 确定一个边界, 然后求解left, right 之间的和, 如果和大于max, 则更新max, 穷举所有的left, right, 最后max即为所求
解法二 : 注意到上面left, right, 求和 会构成一个三层循环, 而求解left, right 之和的过程是可以省略的, 所以这里省略了[left, right]求和, 而更新为累加求和, 之前求和的的一层由 O(n) -> O(1)
解法三 : 分治算法, 讲数组分为两部分, leftArr, rightArr, 则数组中最大的子数组无非下面三种情况, 1. 最大子数组为leftArr的最大子数组, 2. 最大子数组为rightArr的最大子数组, 3. 最大子数组跨越了leftArr 和rightArr
对于前两种情况可以递归处理, 对于第三种情况, 则需要从中间到两边遍历一次, O(n)的复杂度
解法四 : 从左到右, 或者从右到左遍历一次数组, 定义两个变量start, all, start存储”当前子数组”最大值[start上一次小于0的元素, 当前值], all存储整个数组的子数组的最大值
如果start小于0, 则切换”当前子数组” 以当前元素开始, 因为 start序列, curELe 组合的连续序列, 可能的值有以下三种 : 1. start序列, 2. curEle, 3, start序列 + curEle
在上一个循环中, start序列的值大于max, 则保存了max到all中, 而现在 [start序列 + curEle] 显然是小于[start序列], 所以, 我们应该从curEle开始继续向后面遍历, 查找是否存在更大的子序列, 然后更新all
如果start大于0
并且curEle大于0, 将start序列跟新为[start序列 + curEle], 然后判断[start序列 + curEle], 是否大于max, 如果大于, 则将其保存在all中, 继续向前面遍历
如果curEle小于0, 则将start更新为[start序列 + curEle], 因为加上curEle之和绝对不会超过[之前的start序列], 所以可以不用判断其是否大于max, 继续向前遍历
因为只要start大于0, 后面都有可能咸鱼翻身, 成为最大的子序列
4. 代码
/**
* file name : Test21FindMaxSumSeq.java
* created at : 10:44:50 AM May 24, 2015
* created by 970655147
*/
package com.hx.test03;
public class Test21FindMaxSumSeq {
// 找到数组的连续子序列的最大和
public static void main(String []arg) {
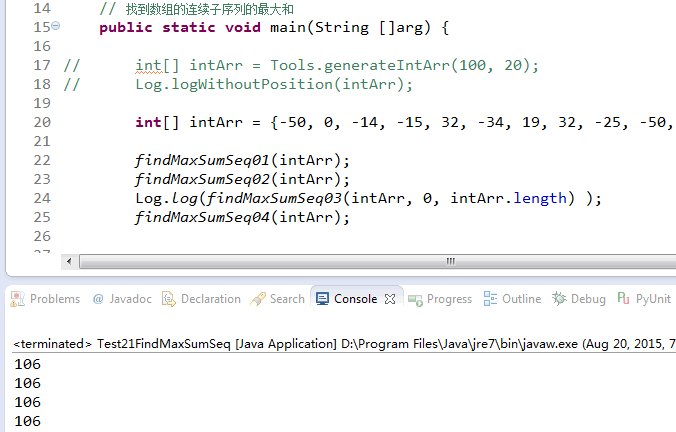
int[] intArr = {-50, 0, -14, -15, 32, -34, 19, 32, -25, -50, 41, -6, 45, 26, -38, 36, -4, -13, -8, -36 };
findMaxSumSeq01(intArr);
findMaxSumSeq02(intArr);
Log.log(findMaxSumSeq03(intArr, 0, intArr.length) );
findMaxSumSeq04(intArr);
}
// 穷举
public static void findMaxSumSeq01(int[] intArr) {
int max = Integer.MIN_VALUE;
for(int i=0; ifor(int j=i+1; jint sum = 0;
for(int k=i; kif(sum > max) {
max = sum;
}
}
}
Log.log(max);
}
// 比上一种解法 优化的地方就是求和
public static void findMaxSumSeq02(int[] intArr) {
int max = Integer.MIN_VALUE;
for(int i=0; iint sum = 0;
for(int j=i; jif(sum > max) {
max = sum;
}
}
}
Log.log(max);
}
// 分而治之, low, high的规则 包头不包尾
// 递归找出左半边, 右半边的最大的子序列
// 找出跨越两半边的最大子序列
// 然后找出 这三者的最大值
// 如果所找只有一个元素 则返回该元素 [退出条件]
public static int findMaxSumSeq03(int[] intArr, int low, int high) {
if(low+1 == high) {
return intArr[low];
}
int mid = (low + high) / 2;
int max01, max02, max03;
max01 = max02 = max03 = Integer.MIN_VALUE;
max01 = findMaxSumSeq03(intArr, low, mid);
max02 = findMaxSumSeq03(intArr, mid, high);
max03 = getMaxSumStrideAcrossTwoSide(intArr, low, mid, high);
int max = getMax(max01, max02, max03);
return max;
}
// 从后向前遍历[从前向后也可以]
// 初始令start, all为最后一个元素
// 然后向前遍历 取start为intArr[i]和intArr[i]+start的较大者[如果start小于0, 则取intArr[i] ]
// 取去all 为当前all, 和当前start子数组之和的最大值
// 如果上一次循环的(start)小于0, 则废弃intArr[lastI], 以及其之前的部分
public static void findMaxSumSeq04(int[] intArr) {
int start = intArr[intArr.length-1], all = start;
for(int i=intArr.length-2; i>=0; i--) {
start = getMax(intArr[i], intArr[i] + start);
all = getMax(all, start);
}
Log.log(all);
}
// 获取两个数的较大者
public static int getMax(int x1, int x2) {
return x1 > x2 ? x1 : x2;
}
// 获取max01, max02, max03的最大值
private static int getMax(int max01, int max02, int max03) {
int max = max01;
if(max02 > max) {
max = max02;
}
if(max03 > max) {
max = max03;
}
return max;
}
// 求解跨越两个区间的 最大值
// 分别找到[low, mid)区间的和的最大值, [mid, high)区间的和的最大值, 然后加起来
// max01 为[low, mid)区间的最大值, max02为[mid, high)取件单恶最大值
private static int getMaxSumStrideAcrossTwoSide(int[] intArr, int low, int mid, int high) {
int max01, max02;
max01 = max02 = Integer.MIN_VALUE;
int sum = 0;
for(int i=mid-1; i>=low; i--) {
sum += intArr[i];
if(sum > max01) {
max01 = sum;
}
}
sum = 0;
for(int i=mid; iif(sum > max02) {
max02 = sum;
}
}
return max01 + max02;
}
}
5. 运行结果
6. 总结
第一种算法的时间复杂度为O(n^3), 因为掺杂和很多冗余的计算
所以第二种算法在在求和的时候做了优化, 使得时间复杂度降了一个级别O(n^2)
分治算法的思路, 使得复杂度降为了O(nlgn)
最后一个思路, 则最为巧妙, 利用了数学知识将时间复杂度降低到了O(n)[遍历一次数组]
注 : 因为作者的水平有限,必然可能出现一些bug, 所以请大家指出!