POJ 2451 nlog(n)半平面交裸题。
Uyuw's Concert
| Time Limit: 6000MS | Memory Limit: 65536K | |
| Total Submissions: 6587 | Accepted: 2611 |
Description
Prince Remmarguts solved the CHESS puzzle successfully. As an award, Uyuw planned to hold a concert in a huge piazza named after its great designer Ihsnayish.
The piazza in UDF - United Delta of Freedom’s downtown was a square of [0, 10000] * [0, 10000]. Some basket chairs had been standing there for years, but in a terrible mess. Look at the following graph.
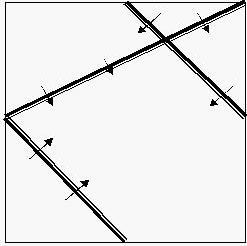
In this case we have three chairs, and the audiences face the direction as what arrows have pointed out. The chairs were old-aged and too heavy to be moved. Princess Remmarguts told the piazza's current owner Mr. UW, to build a large stage inside it. The stage must be as large as possible, but he should also make sure the audience in every position of every chair would be able to see the stage without turning aside (that means the stage is in the forward direction of their own).
To make it simple, the stage could be set highly enough to make sure even thousands of chairs were in front of you, as long as you were facing the stage, you would be able to see the singer / pianist – Uyuw.
Being a mad idolater, can you tell them the maximal size of the stage?
The piazza in UDF - United Delta of Freedom’s downtown was a square of [0, 10000] * [0, 10000]. Some basket chairs had been standing there for years, but in a terrible mess. Look at the following graph.
In this case we have three chairs, and the audiences face the direction as what arrows have pointed out. The chairs were old-aged and too heavy to be moved. Princess Remmarguts told the piazza's current owner Mr. UW, to build a large stage inside it. The stage must be as large as possible, but he should also make sure the audience in every position of every chair would be able to see the stage without turning aside (that means the stage is in the forward direction of their own).
To make it simple, the stage could be set highly enough to make sure even thousands of chairs were in front of you, as long as you were facing the stage, you would be able to see the singer / pianist – Uyuw.
Being a mad idolater, can you tell them the maximal size of the stage?
Input
In the first line, there's a single non-negative integer N (N <= 20000), denoting the number of basket chairs. Each of the following lines contains four floating numbers x1, y1, x2, y2, which means there’s a basket chair on the line segment of (x1, y1) – (x2, y2), and facing to its LEFT (That a point (x, y) is at the LEFT side of this segment means that (x – x1) * (y – y2) – (x – x2) * (y – y1) >= 0).
Output
Output a single floating number, rounded to 1 digit after the decimal point. This is the maximal area of the stage.
Sample Input
3 10000 10000 0 5000 10000 5000 5000 10000 0 5000 5000 0
Sample Output
54166666.7
Hint
Sample input is the same as the graph above, while the correct solution for it is as below:I suggest that you use Extended in pascal and long double in C / C++ to avoid precision error. But the standard program only uses double.
题意:一个区域内,给定若干半平面,求最终围成的区域的面积,
由于数据较大,因此适合nlogn的半平面交,
方法如下:
step1. 将所有半平面按极角排序,对于极角相同的,选择性的保留一个。 O(nlogn)
step2. 使用一个双端队列(deque),加入最开始2个半平面。
step3. 每次考虑一个新的半平面:
a.while deque顶端的两个半平面的交点在当前半平面外:删除deque顶端的半平面
b.while deque底部的两个半平面的交点在当前半平面外:删除deque底部的半平面
c.将新半平面加入deque顶端
step4.删除两端多余的半平面。
具体方法是:
a.while deque顶端的两个半平面的交点在底部半平面外:删除deque顶端的半平面
b.while deque底部的两个半平面的交点在顶端半平面外:删除deque底部的半平面
重复a,b直到不能删除为止。
step5:计算出deque顶端和底部的交点即可。
模拟了半天,有点理解了,
代码:
/* ***********************************************
Author :_rabbit
Created Time :2014/5/4 15:03:55
File Name :20.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include