RL(九)基于策略的强化学习
目录
- 1、策略梯度法与值函数近似法的区别
- 2、为什么使用基于策略(Policy-based )的算法
- 3、 策略目标函数
- 4、评价函数
前面的算法都是基于价值来算的,但是当处理连续动作的问题时,就显得力不从心了,因为我们需要求的Q表太大,根本无法满足我们的需要。前面我们在算法分类的时候也讲过,我们可以按基于价值和基于策略的方式来给RL分类,所以这篇博客就是用基于策略算法来求解强化学习问题。
1、策略梯度法与值函数近似法的区别
值函数近似法:在值函数近似法中,动作选择的策略是不变的,如固定使用ϵ−贪婪法作为策略选择方法。即在时间步t的状态下,选择动作的方式是固定的。
策略梯度法:在策略梯度法中,个体会学习不同的策略。即在某个时间步t的状态下,根据状态的概率分布进行选择,且该动作概率分布可能会不断的调整。可以用下面这个例子来体会一下。
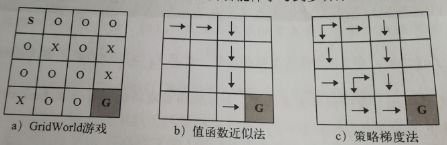
下面这个图是GridWorld环境,目标是使得个体能够从格子S走到格子G,其中,格子X为陷阱,格子O是可行走区域。从图中可以看出值函数近似法只能够得到一条从S到G的路径,但是策略梯度法却可以得到三条。所以值函数近似法的策略是固定的,而策略梯度法的策略能让个体学习多种策略。
2、为什么使用基于策略(Policy-based )的算法
前面讲到基于价值的算法中,我们迭代计算的是值函数,然后根据值函数对策略进行改进;相比基于策略的方法,基于价值的决策部分更为肯定,就选价值最高的,但是也比基于策略的算法多走了一步。而在策略搜索方法中,我们直接对策略进行迭代计算,也就是迭代更新参数值,直到累积回报的期望最大,此时的参数所对应的策略为最优策略。
当然,一个算法肯定是有优点和缺点的,我们先看看基于策略的算法与基于价值的算法相比有哪些优缺点。
优点:
- (1)容易收敛,因为每一次改善都是直接对策略进行改进,而value based时在后期迭代时有时会发生震荡不收敛
- (2)动作空间高维或者连续时更加高效,在value based需要计算所有动作的Q值
- (3)能学到一些随机策略
缺点: - (1)容易收敛到局部最优而不是全局最优
- (2)评价策略时不是很高效而且方差很大
虽然基于策略的算法也还是有缺点,但是经过不断的实践发现,很多时候基于策略的算法比基于价值的算法更好。
3、 策略目标函数
前面我们已经知道策略是一个概率,并不能直接用来迭代,我们要想办法把它变成函数才可以进行迭代,而函数肯定是有参数的,这里我们用θ来表示这个参数。这时候策略就可以用一个关于θ的函数来表示了。这里的θ和前面我们讲的w作用相同,使用不同的符号是为了区分前者作用域基于策略的强化学习任务,后者基于价值的强化学习任务,其实就是用一个函数来逼近我们的策略。
![]()
策略函数为确定时间步t的状态下采取任何可能动作的具体概率,因此可以将 π θ π_θ πθ当做概率密度函数。在实际采取策略动作时可以按该概率分布采样。其中θ决定了概率分布的形态。
现在我们已经知道我们现在的工作就是优化我们的策略函数了,但是怎么去评判我们优化了的策略函数的好坏呢?我们至少得明白往哪方面优化吧,这时就需要一个优化的目标函数,朝着让这个目标函数值最大的方向去优化。目标函数的主要作用是用来衡量策略的好坏程度。
我们的优化目标有几种:
最简单的优化目标就是初始状态收获的期望,即优化目标为:
![]()
但是有的问题是没有明确的初始状态的,那么我们的优化目标可以定义平均价值,即:

其中, d π θ ( s ) d_{πθ}(s) dπθ(s)是基于策略 π θ π_θ πθ生成的马尔科夫链关于状态的静态分布。
或者定义为每一时间步的平均奖励,即:
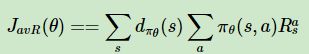
这样就相当于我们量化了我们评价指标。
我们一般常用的优化方法就是梯度上升法,梯度下降法在深度学习里面主要用于寻找损失函数的局部最小值,它的方向是沿着梯度的反方向进行下降的,所以我们的梯度上升法就是按着梯度的正方向进行搜索。
目标函数J(θ)关于参数θ的梯度 ∇ θ J ( θ ) ∇_θJ(θ) ∇θJ(θ)是目标函数上升最快的方向。对于最大化优化问题,只需要将参数θ沿着梯度方向前进一个步长,就可以实现目标函数的下降。这个步长又称为学习速率 α。参数更新公式如下:
θ←θ+Δθ
现在的问题就是怎么求这个梯度 ∇ θ J ( θ ) ∇_θJ(θ) ∇θJ(θ),根据大牛的论文可知:
无论我们是采用 J 1 , J a v V J_1,J_{avV} J1,JavV还是 J a v R J_{avR} JavR来表示优化目标,最终对θ求导的梯度都可以表示为:
![]()
现在我们已经知道对策略函数怎么优化了,但是从上面的式子可以发现,我们策略函数还没有明确的表达式,现在我们就要设计策略函数让它能够真正的运用上面的算法进行优化。
4、评价函数
回顾我们前面关于RL的算法分类讲的关于基于策略的RL的描述, 他能通过感官分析所处的环境,输出下一步要采取的各种动作的概率,根据概率采取行动,所以每种动作都有可能被选中,只是概率不同。仔细分析这句话“要输出下一步要采取的各种动作的概率”,发现和神经网络中的softmax函数的功能一样。
这个函数主要应用于离散空间中,softmax策略使用描述状态和行为的特征ϕ(s,a) 与参数θ的线性组合来权衡一个行为发生的几率,即:

则通过求导很容易求出对应的评价函数为:
![]()
与离散型强化学习任务不同,连续性的强化学习任务通常是和动作或者状态相关的。如自动驾驶的方向和速度必须是相同的,即上一时刻的方向和速度与下一时刻息息相关。所以这时我们采取高斯策略。
通过以上方法,就可以求出最优策略。
其中比较常见的方法是蒙特卡罗策略梯度算法。感兴趣的可以自己去百度学习学习,这里就不在单独列出来了。
通过学习我们发现基于策略和基于价值的算法都有自己的有缺点,能不能把他们的优点结合起来创造一种更好的方法呢?答案是有:Actor-Critic方法。
下一篇:Actor-Critic方法
参考文章:https://www.cnblogs.com/pinard/p/10137696.html
