数据结构与算法（十）线段树(Segment Tree)入门

本文主要包括以下内容：

1. 线段树的概念
2. 线段树的基本操作
3. 实现一个线段树
4. LeetCode相关线段树的问题

线段树的概念

线段树(Segment Tree)也是一棵树，只不过元素的值代表一个区间。
常用区间的 统计 操作，比如一个区间的最大值(max)，最小值(min)，和(sum)等等

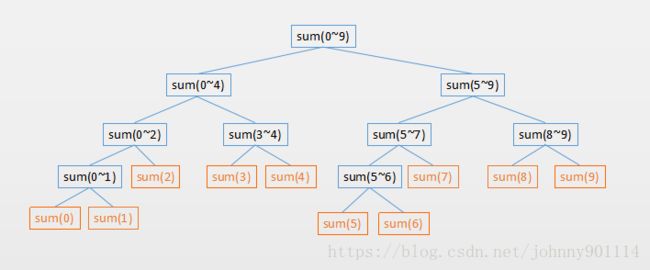
如一个长度为10的数组，它对应的 求和 线段树，如下图所示(图中的数字表示索引)：

根节点就是 0~lenght-1 的和，根节点的左右子树平分根节点的区间，然后依次类推，直到只有一个元素不能划分为止，该元素也就是二叉树的叶子节点。

线段树是一个平衡二叉树，但不一定是完全二叉树。

从上图我们可以得出，求线段树的区间统计，时间复杂度和二叉树的高度有关系，和元素的个数没关系，它的时间复杂度为 O(log n)，如果用普通的遍历的方式它的时间复杂度为 O(n).

如果我们用数组来存储线段树的话，我们大致需要开辟多大的数组空间呢？

根据而前面我们对满二叉树的分析

h层的满二叉树总共有 2^h-1 个节点，第h-1层有2^(h-1)个节点，它们大概是两倍的关系。

也就是说对于满二叉树 最后一层的节点数乘以2 大致就是整棵树的节点数。

但是线段树并不一定是满二叉树，但是一定是平衡二叉树，所以需要多冗余一层。也就是 乘以4 就足以盛放所有的节点数，但是会浪费一定的内存空间。

线段树的基本操作

构建线段树

根据上面我们对线段树的描述，构建一个线段树就比较简单了，根节点就是整个区间，根节点的左右子树平分根节点的区间，直至区间内只剩下一个元素不能平分为止。如下面递归的伪代码：

private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) {
    //如果区间内只剩下一个元素
    if (treeLeft == treeRight) {
        tree[treeIndex] = data[treeLeft];
        return;
    }
    //当前节点左子树索引
    int leftTreeIndex = getLeft(treeIndex);
    //当前节点右子树索引
    int rightTreeIndex = getRight(treeIndex);
    //int mid = (left+right)/2;
    int mid = treeLeft + (treeRight - treeLeft) / 2;
    //构建左子树
    buildSegmentTree(leftTreeIndex, treeLeft, mid);
    //构建右子树
    buildSegmentTree(rightTreeIndex, mid + 1, treeRight);
    //当前节点存放的值，根据具体业务，如果求和就是两个值相加
    //如果是求最大值，那么就存放最大值
    tree[treeIndex] = tree[leftTreeIndex] + tree[rightTreeIndex]

}

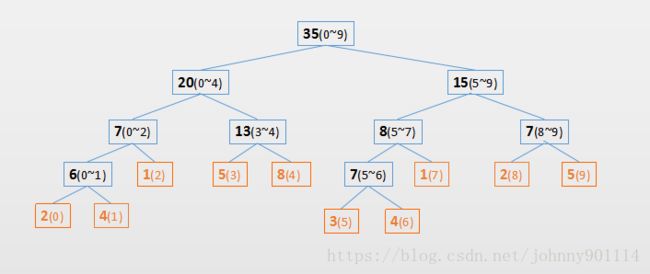
对下面一个数组

就会构建成如下一个线段树(图中括号里数字表示索引区间)

修改线段树

针对上面的数组，把索引为 1 的值改成 6 如下图所示

那么线段树需要修改的节点有(虚线标明)：

线段树的查询

对于线段树的查询，主要有以下几种情况：

1. 要查询的区间在刚好就是当前节点的区间
2. 要查找的区间在当前节点的左子树区间
3. 要查找的区间在当前节点的右子树区间
4. 要查找的区间一部分在当前节点的左子树区间，一部分在右子树区间

实现一个线段树

下面实现的线段树，有三个功能：

1. 把数组构建成一颗线段树
2. 线段树的修改
3. 线段树的查询

public class ArraySegmentTree {

    private T tree[];
    private T data[];

    private Merger merger;

    public interface Merger {
        T merge(T a, T b);
    }

    public ArraySegmentTree(T[] arr, Merger merger) {
        this.merger = merger;
        data = (T[]) new Object[arr.length];
        for (int i = 0; i < data.length; i++) {
            data[i] = arr[i];
        }

        this.tree = (T[]) new Object[data.length * 4];
        buildSegmentTree(0, 0, data.length - 1);

    }


    /**
     * 构建线段树
     *
     * @param treeIndex 当前需要添加节点的索引
     * @param treeLeft  treeIndex左边界
     * @param treeRight treeIndex右边界
     */
    private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) {
        if (treeLeft == treeRight) {
            tree[treeIndex] = data[treeLeft];
            return;
        }
        //当前节点左子树索引
        int leftTreeIndex = getLeft(treeIndex);
        //当前节点右子树索引
        int rightTreeIndex = getRight(treeIndex);
        //int mid = (left+right)/2; 如果left和right很大，可能会导致整型溢出
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        //构建左子树
        buildSegmentTree(leftTreeIndex, treeLeft, mid);
        //构建右子树
        buildSegmentTree(rightTreeIndex, mid + 1, treeRight);
        //当前节点存放的值
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);

    }

    public T query(int start, int end) {
        return query(0, 0, data.length - 1, start, end);
    }

    /**
     * @param treeIndex 当前查找的节点
     * @param treeLeft  treeIndex的左边界
     * @param treeRight treeIndex的右边界
     * @param queryL    用户需要查找的左边界
     * @param queryR    用户需要查找的右边界
     * @return
     */
    private T query(int treeIndex, int treeLeft, int treeRight, int queryL, int queryR) {

        //1, 需要查找的范围完刚好在这个treeIndex节点的区间
        if (treeLeft == queryL && treeRight == queryR) {
            return tree[treeIndex];
        }

        //当前节点的区间的中间点
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        //左子树索引
        int leftTreeIndex = getLeft(treeIndex);
        //右子树索引
        int rightTreeIndex = getRight(treeIndex);


        //2, 需要查找的范围完全在左子树的区间里
        if (queryR <= mid) {
            return query(leftTreeIndex, treeLeft, mid, queryL, queryR);
        }
        //3, 需要查找的范围完全在右子树区间里
        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, treeRight, queryL, queryR);
        }

        //需要查找的范围一部分在左子树里，一部分在右子树中
        T left = query(leftTreeIndex, treeLeft, mid, queryL, mid);
        T right = query(rightTreeIndex, mid + 1, treeRight, mid + 1, queryR);
        return merger.merge(left, right);
    }
    
    
    public void update(int index, T e) {
        data[index] = e;
        update(0, 0, data.length - 1, index, e);
    }


    private void update(int treeIndex, int treeLeft, int treeRight, int index, T e) {
        if (treeLeft == treeRight) {
            tree[treeIndex] = e;
            return;
        }

        int mid = treeLeft + (treeRight - treeLeft) / 2;
        int leftChildIndex = getLeft(treeIndex);
        int rightChildIndex = getRight(treeIndex);

        if (index <= mid) {
            update(leftChildIndex, treeLeft, mid, index, e);
        } else if (index >= mid + 1) {
            update(rightChildIndex, mid + 1, treeRight, index, e);
        }

        //更改完叶子节点后，还需要对他的所有祖辈节点更新
        tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
    }

    public T get(int index) {
        return data[0];
    }

    public int size() {
        return data.length;
    }

    public int getLeft(int index) {
        return index * 2 + 1;
    }

    public int getRight(int index) {
        return index * 2 + 2;
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        builder.append("[");
        for (int i = 0; i < tree.length; i++) {
            if (tree[i] == null) {
                continue;
            }
            builder.append(tree[i]).append(',');
        }
        builder.deleteCharAt(builder.length() - 1);
        builder.append(']');
        return builder.toString();
    }
}

LeetCode关于线段树的问题

LeetCode第303号问题

问题描述： 给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

问题示例：

给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange(int i, int j)

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

问题说明：

你可以假设数组不可变。
会多次调用 sumRange 方法。

对于这个问题，在脑海中的方案就是遍历区间[i,j]，然后累加

class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }

    public int sumRange(int i, int j) {
        int sum = 0;
        for (int k = i; k <= j; k++) {
            sum += nums[k];
        }
        return sum;
    }
}

把这个代码提交给LeetCode，最后提示我们的代码超时了。

原因在于LeetCode会构建一个很长的数组，然后调用很次sumRange，每次调用区间都不一样。这些操作没有在规定的时间内执行完毕，超时了。

这个时候就可以用线段树来解决这个问题，对我们实现的线段树代码做一些修改以适应LeetCode代码规范

class NumArray {
    
    private int tree[];
    private int[] data;

    public NumArray(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }
        data = new int[arr.length];
        for (int i = 0; i < data.length; i++) {
            data[i] = arr[i];
        }

        this.tree = new int[data.length * 4];
        buildSegmentTree(0, 0, data.length - 1);
    }

    private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) {
        if (treeLeft == treeRight) {
            tree[treeIndex] = data[treeLeft];
            return;
        }
        int leftTreeIndex = getLeft(treeIndex);
        int rightTreeIndex = getRight(treeIndex);
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        buildSegmentTree(leftTreeIndex, treeLeft, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, treeRight);
        tree[treeIndex] = (tree[leftTreeIndex] + tree[rightTreeIndex]);

    }

    public int query(int start, int end) {
        return query(0, 0, data.length - 1, start, end);
    }

    private int query(int treeIndex, int treeLeft, int treeRight, int queryL, int queryR) {
        if (treeLeft == queryL && treeRight == queryR) {
            return tree[treeIndex];
        }
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        int leftTreeIndex = getLeft(treeIndex);
        int rightTreeIndex = getRight(treeIndex);
        if (queryR <= mid) {
            return query(leftTreeIndex, treeLeft, mid, queryL, queryR);
        }
        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, treeRight, queryL, queryR);
        }
        int left = query(leftTreeIndex, treeLeft, mid, queryL, mid);
        int right = query(rightTreeIndex, mid + 1, treeRight, mid + 1, queryR);
        return left + right;
    }


    public int getLeft(int index) {
        return index * 2 + 1;
    }

    public int getRight(int index) {
        return index * 2 + 2;
    }

    public int sumRange(int i, int j) {
        return query(i, j);
    }
}

最后获得了LeetCode的通过。

LeatCode 307号问题

这个问题和上面的303号问题基本一样，唯一不同的是需要修改数组里的元素。

问题描述：

给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。

问题示例：

示例:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

问题说明：

数组仅可以在 update 函数下进行修改。
你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。

这个问题，在上一个问题代码的基础上，调用我们线段树的update方法即可。由于篇幅的原因，代码就不贴出来了

有需要的可以查看我的github

Reference

本文主要内容和大纲是学习了慕课网 liuyubobobo 老师的视频《算法大神带你玩转数据结构 从入门到精通》
有需要的同学可以看看, 真心不错. 墙裂推荐… 最好能加上自己的思考和理解.

---

下面是我的公众号，干货文章不错过，有需要的可以关注下，有任何问题可以联系我：

本文相关代码